Скорость. Для характеристики быстроты движения материальной точки вводят векторную физическую величину – скорость.

Для характеристики быстроты движения материальной точки вводят векторную физическую величину – скорость.

Пусть в момент t₁ материальная точка, движущая по некоторой траектории, находилась в положении А (x ₁, y ₁, z ₁), характеризуемом радиус– вектором 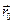, в момент времени t₂ – в положении В (x ₂, y ₂, z ₂), характеризуемом радиус – вектором 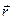(рис. 1.2). Таким образом, за интервал времени Dt= t₂- t₁ материальная точка прошла криволинейный отрезок АВ =D S.

Вектором средней скорости 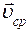точки в интервале от t₁ до t₂ называется

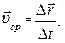
(1.1.3)

Из формулы (1.1.3) видно, что вектор средней скорости 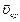совпадает по направлению с вектором перемещения 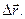При неограниченном уменьшении времени, т.е. Dt ® 0, то средняя скорость стремиться к предельному значению, которое называется мгновенной скоростью

.

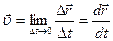(1.1.4)

Вектор мгновенной скорости направлен по касательной к данной точки траектории. Из математики известно, что при DS ® 0 DS/Dr = 1 и, как следствие, 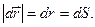В этом случае можно ввести понятие путевой скорости:

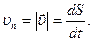(1.1.5)

Из уравнения (1.1.5) можно определить путь, пройденный точкой за данный промежуток времени: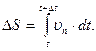

Поскольку мгновенная скорость 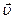- векторная величина, то ее можно разложить на три составляющие по осям координат, то есть

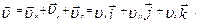
(1.1.6)

Используя выражения (1.1.1) и (1.1.4), можно показать, что

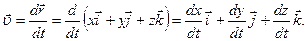
(1.1.7)

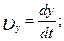
Сравнивая выражения (1.1.6) и (1.1.7), можно определить проекции вектора скорости на декартовые оси координат: 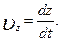Последние позволяют рассчитать модуль скорости в данный момент времени:

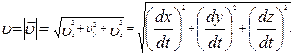
В системе СИ единицей измерения скорости является

Ускорение

Величиной, характеризующей быстроту изменения скорости, является ускорение.

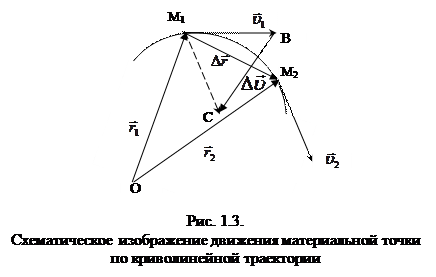На рисунке 1.3. показан участок траектории движения материальной точки. Пусть в момент времени t₁ материальная точка находилась в положении М₁ и двигалась со скоростью 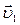, в момент времени t₁ – в М₂ и имела скорость . Изменение скорости за интервал времени Dt: 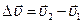(на рис. 1.3. 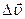соответствует вектору ).

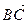Средним ускорением неравномерного движения в интервале Dt называется векторная величина, равная отношению изменения скорости 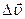к интервалу времени

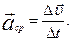
(1.1.8)

Как видно из формулы, вектор среднего ускорения сонаправлен с вектором изменения скорости .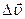

Ускорением или мгновенным ускорением точки в момент времени t называется величина

(1.1.9)

Так как мгновенное ускорение – векторная величина, то

(1.1.10)

Из выражений (1.1.6) и (1.1.9) следует 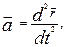и, как следствие:

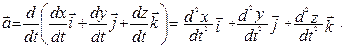
(1.1.11)

Таким образом, из (1.1.10) и (1.1.11) следует, что

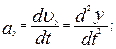
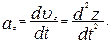
Модуль вектора ускорения равен

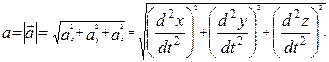
При рассмотрении плоского движения удобно пользоваться скользящей системой координат – системой, которая изменяет свое положение в пространстве вместе с движением материальной точки, то есть за начало отсчета принимают саму движущуюся точку. Одна ось вышеуказанной системы направлена по касательной к траектории движения материальной точки в данный момент времени (тангенциальная или касательная ось 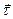), другая направлена перпендикулярно первой, и называется нормальной осью (см. рис. 1.4).

Рассмотрим движение точки вдоль криволинейной траектории MN (см. рис.1.4). В скользящей системе координат скорость материальной точки можно представить как 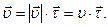Из выражения (1.1.9) следует, что

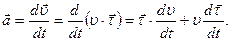
Таким образом, ускорение материальной точки представляет собой сумму двух векторов:

1) тангенциальное ускорение, которое показывает быстроту изменение модуля скорости материальной точки:

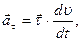
2) нормальное ускорение показывает быстроту изменения направления скорости:

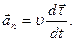
Величина полного ускорения

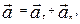
(1.1.12)

Нормальное ускорение перпендикулярно тангенциальной оси и направлено по нормальной оси скользящей системы координат.

Для определения физического смысла нормального ускорения рассмотрим равномерное движение материальной точки по окружности (см. рис. 1.5). В момент времени t₁ материальная точка находилась в положении М₁ и двигалась со скоростью – , в момент t₂ – в положении М₂ и имела скорость 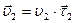. При равномерном движении модуль скорости остается постоянным (следовательно, тангенциальное ускорение равно нулю: 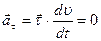), а направление вектора скорости меняется. Изменение единичного вектора равно . За малый промежуток времени dt модуль вектора dt можно определить как dt = t×dj, где dj - угол поворота вектора скорости материальной точки. Так как t = 1, то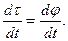

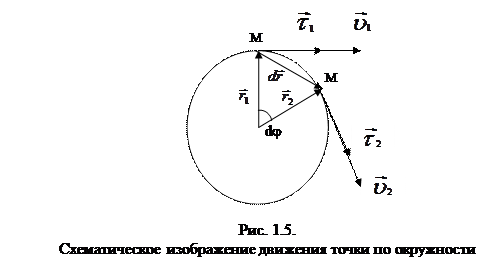Из рис. 1.5 видно, что dr =R×dj (R – радиус окружности).

Поэтому 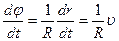. Из приведенных выше выводов следует, что

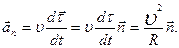
(1.1.13)

При прямолинейном движении нормальная составляющая полного ускорения равна нулю (так как 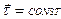и ). При равномерном движении по окружности, как отмечалось выше, 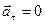. В общем случае при криволинейном движении имеют место и тангенциальная и нормальная составляющие полного ускорения, так что можно определить модуль полного ускорения: Единицей измерения ускорения в системе СИ является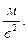

Рассмотрим несколько частных случаев:

1. Прямолинейное равномерное движение:

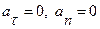, , причем 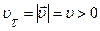. Поэтому

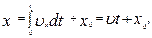
(1.1.14,а)

где x ₀ – значение x в начальный момент времени (t = 0). Таким образом, для величины пути

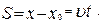
(1.1.14,б)

2. Прямолинейное равнопеременное движение:

a _n = 0, a _t = const. При a _t > 0 – движение равноускоренное; при a _t < 0 – движение равнозамедленное.

Из выражения (1.1.9) следует, что

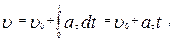
(1.1.15)

где – начальная скорость. Для координаты

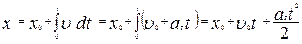
(1.1.16,а)

и пути

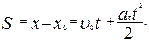
(1.1.16,б)

Часто для простоты записи в выражениях (1.1.15), (1.1.16,а) и (1.1.16,б) вместо a _t используют a.

3. Равномерное движение по окружности:

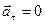, a _n = const. Так как численное значение скорости в этом виде движения является постоянной величиной, то величина скорости может быть определена через 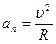. При R=const траектория движения является окружность. В этом случае ускорение a _n называют центростремительным.

4) a_n = const, a_τ = const – траекторией движения является спираль.

Дата добавления: 2014-11-18