
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Урок № 17
|
|
|
|
Тема: Загальна схема побудови графіків функцій.
План:
1. Дослідження функцій за першою похідною.
2. Дослідження функцій за другою похідною.
3. Загальна схема дослідження функцій.
Теорема 1. (достатня умова зростання (спадання) графіка функції). Якщо функція  , має додатню (від’ємну) похідну в кожній точці інтервала
, має додатню (від’ємну) похідну в кожній точці інтервала  , то ця функція зростає (спадає) на цьому інтервалі.
, то ця функція зростає (спадає) на цьому інтервалі.



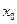
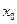 Теорема 2. (достатня умова існування екстремума функції). Нехай функція неперервна в точці і в деякому її околі має похідну, крім, можливо, самої точки. Тоді:1) якщо похідна при переході через точку змінює знак з “+” на “-“, то точка є точкою максимума; 2) якщо похідна
Теорема 2. (достатня умова існування екстремума функції). Нехай функція неперервна в точці і в деякому її околі має похідну, крім, можливо, самої точки. Тоді:1) якщо похідна при переході через точку змінює знак з “+” на “-“, то точка є точкою максимума; 2) якщо похідна 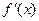 при переході через точку змінює знак з “-” на “+“, то точка є точкою мінімума; 3) якщо похідна при переході через точку не змінює знак, то в точці функція не має екстремума.
при переході через точку змінює знак з “-” на “+“, то точка є точкою мінімума; 3) якщо похідна при переході через точку не змінює знак, то в точці функція не має екстремума.
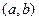
 Теорема 3. (достатня умова випуклості графіка функції). Якщо на інтервалі двічі диференційована функція має від’ємну (додатню) другу похідну, то графік функції випуклий вгору (вниз).
Теорема 3. (достатня умова випуклості графіка функції). Якщо на інтервалі двічі диференційована функція має від’ємну (додатню) другу похідну, то графік функції випуклий вгору (вниз).
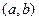

 Теорема 4. (достатня умова існування перегину графіка функції). Якщо функція двічі диференційована на інтервалі і при переході через точку друга похідна змінює знак, то ця точка кривої є точкою перегину.
Теорема 4. (достатня умова існування перегину графіка функції). Якщо функція двічі диференційована на інтервалі і при переході через точку друга похідна змінює знак, то ця точка кривої є точкою перегину.
Схема дослідження функцій і побудови їхніх графіків:
1. Знайти область визначення функції.
2. Встановити парність (непарність) і періодичність функції.
3. Знайти точки розриву функції та їх характер.
4. Визначити точки перетину графіка функції з осями координат.
5. Знайти точки екстремуму та обчислити значення функції у цих точках.
6. Визначити інтервали зростання й спадання функції.
7. Знайти точки перегину, інтервали випуклості й вгнутості.
|
|
|
8. Знайти асимптоти.
9. Знайти граничні значення функції, коли х прямує до граничних точок області визначення.
Графік функції будують за характерними точками й лініями, отриманими у результаті дослідження. Якщо їх недостатньо, знаходять допоміжні точки для деяких конкретних значень аргументу.
Приклад. Дослідити функцію 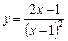 і побудувати її графік.
і побудувати її графік.
l 1. Знаходимо область визначення функції. Функція існує при всіх значеннях х за винятком значення х = 1. Звідси її область визначення 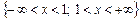 .
.
2. Точка х = 1 є точкою розриву функції. Дослідимо її характер:
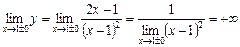 .
.
Як ліворуч, так і праворуч точки х = 1 маємо нескінченний розрив.
Точка х = 1 — точка розриву другого роду.
3. Вертикальні асимптоти. Пряма х = 1 є вертикальною асимптотою.
4. Знаходимо точки перетину графіка функції з осями координат: з віссю Ох: у = 0,  ; з віссю Оу: х = 0,
; з віссю Оу: х = 0, 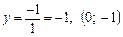 .
.
5. Знаходимо точки екстремуму та інтервали зростання і спадання функції, результати заносимо у табл. 4.3:
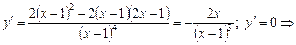
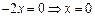 — критична точка. При
— критична точка. При 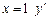 не існує, але у цій точці сама функція теж не існує. Дослідимо критичну точку
не існує, але у цій точці сама функція теж не існує. Дослідимо критичну точку
х = 0 на екстремум:
при  ;
;
при 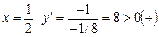 .
.
Таблиця 17.1
| х | 
| (0, 1) | 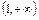
| ||
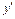
| – | + | Не існує | – | |
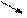   у у
| y min (–1) | Не існує |
Проходячи через критичну точку зліва направо, перша похідна змінює знак з «–» на «+», через це в точці х = 0 функція має мінімум:
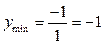 .
.
У точці х = 1 функція не визначена. При 
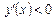 , отже, функція на цьому інтервалі спадає.
, отже, функція на цьому інтервалі спадає.
6. Точки перегину та інтервали опуклості й вгнутості графіка функції знаходимо за допомогою другої похідної:
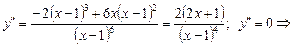
 ; при х = 1
; при х = 1  не існує, але в цій точці не існує і сама функція.
не існує, але в цій точці не існує і сама функція.
Дослідимо точку 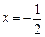 :
:
при  ;
;
при 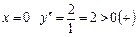 .
.
Друга похідна, проходячи через 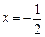 , змінює знак, отже, точка перетину кривої з цією абсцисою є точкою перегину.
, змінює знак, отже, точка перетину кривої з цією абсцисою є точкою перегину.
Знайдемо її ординату:
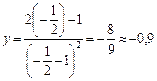 .
.
Таким чином, точка  — точка перегину.
— точка перегину.
У точці х = 1 функція не визначена. При  , значить, графік функції вгнутий.
, значить, графік функції вгнутий.
Результати дослідження заносимо у табл. 17.2
|
|
|
Таблиця 17.2
| х | 
| 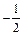
| 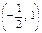
| 
| 
|

| + | + | Не існує | + | |
| у | Ç | Перегин (– 8/9) | È | Не існує | È |
7. Рівняння похилої асимптоти знаходимо у вигляді 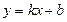 :
:


Таким чином, похилою асимптотою є у = 0 (вісь Ох).
На підставі результатів дослідження будуємо графік функції. Для точнішої побудови візьмемо додатково точки на рис. 17.1: (–5; – 0,3),  , (2; 3), (3; 1,3).
, (2; 3), (3; 1,3).

Рис. 17.1
Завдання. Дослідити функцію та побудувати її графік:

 ;
;  ;
;  .
.
Контрольні запитання:
1. Як за першою похідною визначити характер монотоності функції?
2. Коли критична точка першого роду буде точкою екстремума?
3. Яка характеристика графіка функції визначається за допомогою другої похідної?
4. В якому випадку критична точка другого роду буде точкою перегину?
5. За якою схемою досліджують функцію?
Література: [1] – с.232-236
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 434; Нарушение авторских прав?; Мы поможем в написании вашей работы!