Основные формулы и определения

КИНЕМАТИКА ЖИДКОСТИ

КОНТРОЛЬНАЯ РАБОТА

Таблица вариантов

Вариант	Номера задач
	1.1	1.11	2.1	2.11	3.1	3.11	3.21	3.31	3.41	4.1
	1.2	1.12	2.2	2.12	3.2	3.12	3.22	3.32	3.42	4.2
	1.3	1.13	2.3	2.13	3.3	3.13	3.23	3.33	3.43	4.3
	1.4	1.14	2.4	2.14	3.4	3.14	3.24	3.34	3.44	4.4
	1.5	1.15	2.5	2.15	3.5	3.15	3.25	3.35	3.45	4.5
	1.6	1.16	2.6	2.16	3.6	3.16	3.26	3.36	3.46	4.6
	1.7	1.17	2.7	2.17	3.7	3.17	3.27	3.37	3.47	4.7
	1.8	1.18	2.8	2.18	3.8	3.18	3.28	3.38	3.48	4.8
	1.9	1.19	2.9	2.19	3.9	3.19	3.29	3.39	3.49	4.9
	1.10	1.20	2.10	2.20	3.10	3.20	3.30	3.40	3.50	4.10

При изучении движения жидкости преимущественное распространение получил метод Эйлера, согласно которому рассматривают поле скоростей в точках пространства, занятого движущейся жидкостью. Поле скоростей задается в следующем виде:

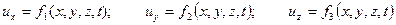
(1.1)

где u_x, u_y, u_z – проекции скорости на декартовы оси координат;

х, у, z – координаты точек пространств;

t – время.

К числу важнейших понятий в кинематике относятся понятия о линиях тока и траекториях движущихся частиц.

Линиями тока называют векторные линии поля скоростей, то есть кривые, в каждой точке которых в данный момент времени вектор скорости совпадает по направлению с касательной.

Дифференциальное уравнение линий тока имеет вид:

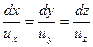
(1.2)

Под траекторией понимают геометрическое место последовательных положений движущейся частицы в рассматриваемой системе координат.

Уравнение траекторий записывается следующим образом:

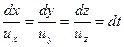
(1.3)

При установившемся движении траектории и линии тока совпадают. Проекции ускорения жидкой частицы на декартовы оси координат в переменных Эйлера определяются из соотношений:

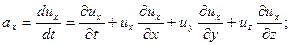
	(1.3)

Первые члены правых частей системы уравнений (1.3) отражают изменение проекций скоростей данной точке пространства из-за нестанционарности поля скоростей и носят название локальных ускорений, остальные члены связаны с неоднородностью поля скоростей и называются конвективными ускорениями.

Закон сохранения массы в гидромеханике в обще случае представляется в виде уравнения неразрывности (сплошности) , где ρ – плотность жидкости. Для несжимаемой жидкости уравнение неразрывности 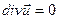, или в проекциях на декартовы оси координат:

(1.4)

Поток вектора скорости через поверхность S называется объемным расходом и является скалярной величиной, определяемой по формуле , где 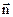- нормаль к поверхности.

Совокупность линий тока, проходящих через все точки бесконечно малого замкнутого контура, образует поверхность, называемую трубкой тока. Жидкость, заключенная внутри трубки тока, называется струйкой.

Уравнение сплошности для струйки несжимаемой жидкости имеет следующий вид

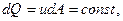
(1.5)

где dQ – элементарный объемный расход через поперечное сечение струйки; dA – площадь сечения струйки.

Угловая скорость вращения жид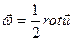кой частицы , - вихрь вектора скорости жидкой частицы.

В проекциях на декартовы оси координат:

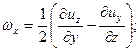
	(1.6)

При потенциальном (безвихревом) движении вихрь вектора скорости:

(1.7)

В координатной форме вихрь вектора скорости имеет вид:

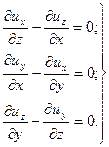
(1.8)

В потенциальном поле существует скалярная функция φ, связанная с вектором скорости зависимостью: u = grad φ, называемая потенциалом скорости.

Условия Коши-Римана:

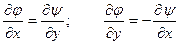
(1.9)

Для решения практических задач широко используется метод наложения потенциальных потоков, который является следствием линейности уравнения Лапласа.

Дата добавления: 2014-11-18