
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Функцій
|
|
|
|
8.1. Похідна від тригонометричних функцій.
Теорема 8.1. Якщо 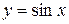 , то
, то 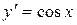 .
.
Доведення. Дамо аргументові х приріст 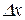 . Тоді можна записати
. Тоді можна записати
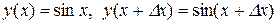
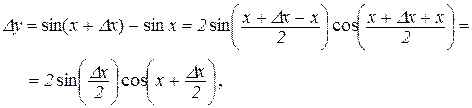
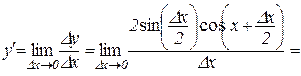
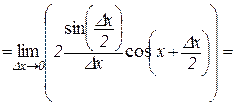
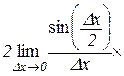
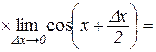
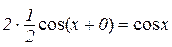 .
.
Обчислюючи дві останні границі, ми використали першу “чудову” границю і те, що функція 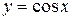 неперервна.
неперервна.
Таким чином, 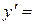 cos x і теорему доведено
cos x і теорему доведено 
Теорема 8.2. Якщо 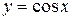 , то
, то 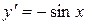 .
.
Доведення. Аналогічно попередній теоремі маємо
 ,
,

 ,
,
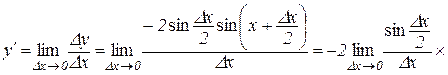
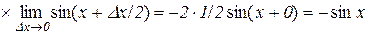 ,
,
тобто 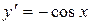
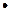
Теорема 8.3. Якщо 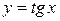 , то
, то  .
.
Доведення. Використаємо теорему 7.4, тобто формулу про похідну від відношення двох функцій:
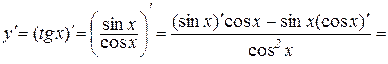
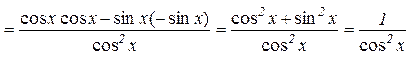 .
.
Таким чином, 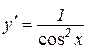
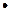
Теорема 8.4. Якщо 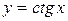 , то
, то 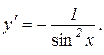
Доведення. Аналогічно попередній теоремі отримуємо
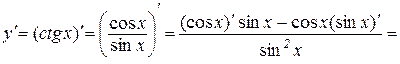
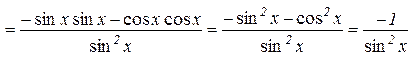 ,
,
таким чином 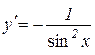
8.2. Похідна логарифмічної функції.
Теорема 8.5. Якщо  , то
, то 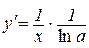 .
.
Доведення. Надамо аргументові х приріст 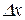 . Тоді
. Тоді
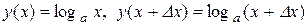 ,
,
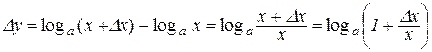 ,
,
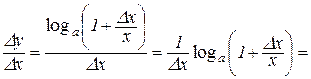
 ,
,
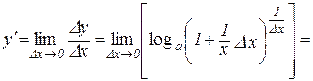
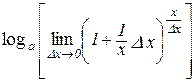 .
.
В останньому перетворенні ми використали неперервність функції  . Введемо нову змінну
. Введемо нову змінну  . Очевидно, що
. Очевидно, що 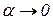 при
при 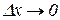 . Тоді з наслідку 4.2.2 до другої “чудової” границі, де
. Тоді з наслідку 4.2.2 до другої “чудової” границі, де 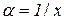 і
і 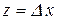 можна записати:
можна записати:

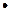
Наслідок. 8.5. Якщо 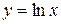 , то
, то 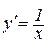
Дійсно, при а=е маємо 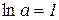
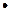
Теорема 8.6. Якщо 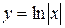 , то
, то 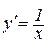 .
.
Доведення. а) Якщо x>0, то 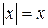 і
і 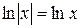 , тому
, тому 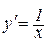 ;
;
б) Нехай x<0, тоді 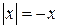 і
і 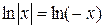 . Зауважимо, що
. Зауважимо, що 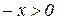 при x<0. Таким чином, для функції
при x<0. Таким чином, для функції 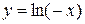 одержуємо
одержуємо
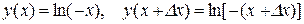 ;
;
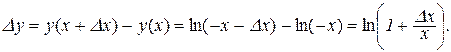 .
.
Далі аналогічно доведенню теореми 8.5 дістаємо
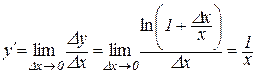 .
.
Таким чином, для від’ємних значень х також справджується рівність 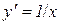 , тобто теорему доведено для будь-яких
, тобто теорему доведено для будь-яких 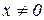 . При х=0 функція
. При х=0 функція 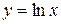 невизначена
невизначена 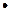
8.3. Похідна складної функції.
Розглянемо складну функцію 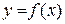 , тобто функцію, яку можна подати у вигляді:
, тобто функцію, яку можна подати у вигляді: 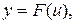 де
де 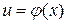 ; або
; або 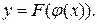 Тут
Тут 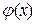 ,
, 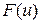 – відповідно внутрішня і зовнішняфункція, u – проміжнийаргумент.
– відповідно внутрішня і зовнішняфункція, u – проміжнийаргумент.
Виведемо правило диференціювання складної функції.
Теорема 8.7. Якщо функція 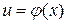 має в деякій точці х похідну
має в деякій точці х похідну 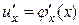 , а функція
, а функція 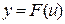 має за відповідного значення
має за відповідного значення 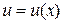 похідну
похідну 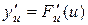 , то складна функція
, то складна функція 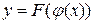 в точці х має похідну
в точці х має похідну 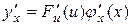 .
.
|
|
|
Іншими словами, похідна складної функції дорівнює добутку похідної зовнішньої функції по проміжному аргументу на похідну проміжного аргументу по незалежній змінній.
Після обчислення похідної в останній вираз замість u потрібно підставити функцію 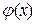 .
.
Доведення. Для значень аргументу х і 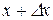 маємо
маємо
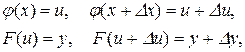
тобто приросту 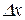 відповідає приріст
відповідає приріст 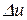 , якому в свою чергу відповідає приріст
, якому в свою чергу відповідає приріст 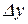 . Зауважимо, що при
. Зауважимо, що при 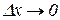 вирази
вирази 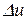 і
і 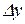 теж прямують до нуля, так як
теж прямують до нуля, так як 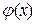 і
і 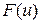 диференційовані функції
диференційовані функції
За умовою теореми
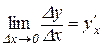 .
.
Тому за теоремою 3.1 можна записати:
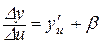 або
або 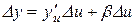 ,
,
де 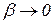 при
при 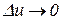 . Розділимо обидві частини останньої рівності на
. Розділимо обидві частини останньої рівності на 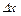 і перейдемо до границі при
і перейдемо до границі при 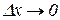 :
:
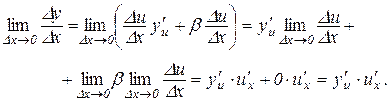
Таким чином, 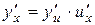 і теорему доведено
і теорему доведено 
Приклад 8.1. Знайти похідну функції 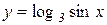 .
.
Розв’язування. Запишемо задану функцію у вигляді 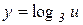 , де
, де 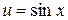 . Тоді за теоремою 8.7 отримаємо
. Тоді за теоремою 8.7 отримаємо
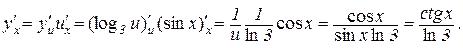 .
.
Приклад 8.2. Знайти похідну функції 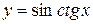 .
.
Розв’язування. Аналогічно попередньому прикладу маємо (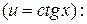 ):
):
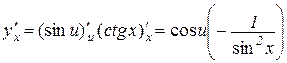
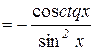 .
.
8.4. Похідна функції, заданої неявно.
Нехай залежність між двома змінними х і у задана деяким рівнянням, яке символічно можна записати у вигляді
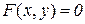 . (8.1)
. (8.1)
Розглянемо функцію 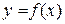 , визначену в деякому інтервалі
, визначену в деякому інтервалі 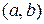 . Якщо рівняння (8.1) при підстановці в ньому замість змінної у виразу
. Якщо рівняння (8.1) при підстановці в ньому замість змінної у виразу 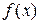 перетворюється в тотожність, то воно є неявним заданням функції
перетворюється в тотожність, то воно є неявним заданням функції 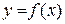 і його інколи записують у вигляді
і його інколи записують у вигляді
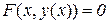 .
.
Наприклад: 1) 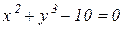 ; 2)
; 2) 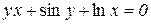 .
.
В першому прикладі можна перейти від неявно заданої функції до явно заданої: 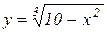 .
.
Покажемо на прикладі як обчислюється похідна від функції заданої неявно.
Нехай задана функція 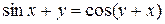 , де
, де 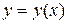 , тобто
, тобто  .
.
Продиференціюємо останню рівність, враховуючи, що cos(y(x)+x) складна функція:

або
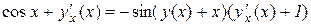 .
.
З останньої рівності виражаємо похідну 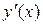 :
:
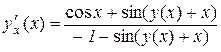
або
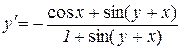 .
.
8.5. Похідна степеневої і показникової функцій.
Теорема 8.8. Похідна функції 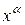 , де
, де 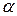 – довільне дійсне число, дорівнює
– довільне дійсне число, дорівнює 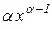 , тобто
, тобто
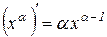 .
.
Доведення. Логарифмуючи функцію 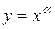 на її області визначення, отримаємо
на її області визначення, отримаємо
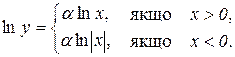 (8.2)
(8.2)
Продиференціюємо обидві частини рівності (8.2) маючи на увазі, що 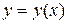 і
і  є складною функцією:
є складною функцією:
|
|
|
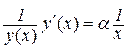
або
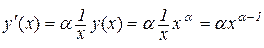
Теорема 8.9. Якщо 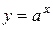 , де a>0, то
, де a>0, то 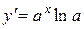 .
.
Доведення. Прологарифмуємо функцію 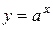 :
:
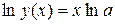 .
.
Диференціювання останньої рівності дає
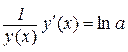 або
або 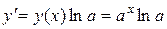
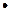
Наслідок. 8.9. Якщо 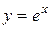 , то
, то 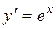
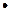
Теорема 8.10. Якщо 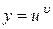 , де
, де 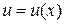 і
і 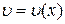 , то
, то
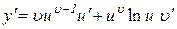 .
.
Доведення. Прологарифмуємо функцію 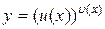 :
:
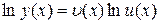 .
.
Диференціювання останньої рівності дає

або
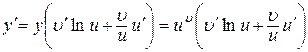 ;
;
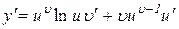
Приклад 8.3. Знайти похідну функції 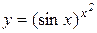 .
.
Розв’язування. За теоремою 8.10 отримуємо
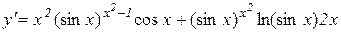 .
.
8.6. Поняття оберненої функції та її похідна.
Розглянемо зростаючу функцію 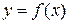 , визначену на деякому інтервалі
, визначену на деякому інтервалі 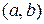 , і нехай
, і нехай 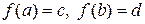 . Оскільки функція зростаюча, то для двох довільних значень х1 і х2 з інтервалу
. Оскільки функція зростаюча, то для двох довільних значень х1 і х2 з інтервалу 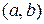 , таких що x1<x2 , виконуватиметься нерівність
, таких що x1<x2 , виконуватиметься нерівність 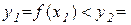
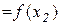 . Тобто двом різним значенням х1 і х2 змінної х відповідатимуть різні значення у1 і у2 змінної у. Справедливе і обернене твердження: якщо y1<y2 і
. Тобто двом різним значенням х1 і х2 змінної х відповідатимуть різні значення у1 і у2 змінної у. Справедливе і обернене твердження: якщо y1<y2 і 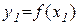 ,
, 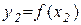 , то х1<x2 . Отже, між значеннями змінних х і у встановлена взаємно однозначна відповідність.
, то х1<x2 . Отже, між значеннями змінних х і у встановлена взаємно однозначна відповідність.
Якщо тепер значення змінної 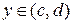 розглядати як значення аргументу, а значення х як значення функції, то можна записати:
розглядати як значення аргументу, а значення х як значення функції, то можна записати: 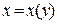 .
.
Функція 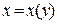 називається оберненою для функції
називається оберненою для функції 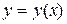 . Очевидно, що функція
. Очевидно, що функція 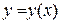 є оберненою для функції
є оберненою для функції 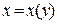 . Аналогічні міркування справедливі і для спадної функції. Зауважимо (без доведення): якщо монотонна функція
. Аналогічні міркування справедливі і для спадної функції. Зауважимо (без доведення): якщо монотонна функція 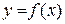 неперервна на відрізку
неперервна на відрізку 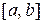 , причому
, причому  , то обернена функція
, то обернена функція 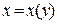 визначена і неперервна на відрізку
визначена і неперервна на відрізку 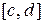 . Якщо функція не є монотонною на деякому інтервалі, то на цьому інтервалі вона може мати декілька обернених функцій.
. Якщо функція не є монотонною на деякому інтервалі, то на цьому інтервалі вона може мати декілька обернених функцій.
Приклад 8.4. Функція 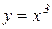 – зростаюча на проміжку
– зростаюча на проміжку 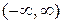 . Вона має обернену функцію
. Вона має обернену функцію 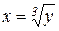 .
.
Приклад 8.5. Функція 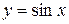 – зростаюча на проміжку
– зростаюча на проміжку 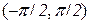 і має обернену функцію
і має обернену функцію 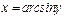 на проміжку
на проміжку 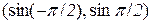 або (–1;1).
або (–1;1).
Приклад 8.6. Функція  визначена на проміжку
визначена на проміжку 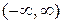 , але не є на ньому ні зростаючою, ні спадною. Вона зростає на проміжку
, але не є на ньому ні зростаючою, ні спадною. Вона зростає на проміжку 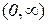 , тому тут існує обернена функція
, тому тут існує обернена функція 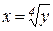 . На проміжку
. На проміжку 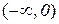 функція
функція  спадна і також має обернену функцію, але
спадна і також має обернену функцію, але 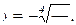 .
.
Розглянемо диференціювання оберненої функції.
Теорема 8.11. Якщо для функції 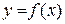 існує обернена функція
існує обернена функція 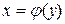 , яка в точці у має відмінну від нуля похідну
, яка в точці у має відмінну від нуля похідну 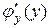 , то у відповідній точці х функція
, то у відповідній точці х функція 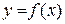 має похідну
має похідну 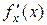 , що дорівнює
, що дорівнює 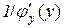 , тобто справедлива формула
, тобто справедлива формула
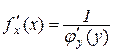 , (8.3)
, (8.3)
Доведення. Продиференціюємо обидві частини рівності 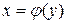 по змінній х, враховуючи, що у є функцією від х, тобто
по змінній х, враховуючи, що у є функцією від х, тобто 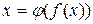 :
:
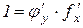 (8.4)
(8.4)
або
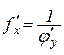 .
.
Рівність (8.4) отримали з використанням теореми 8.7 для складної функції 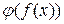 .
.
|
|
|
Таким чином, теорему доведено 
Зауваження 8.1. Після диференціювання по змінній у в функції 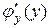 необхідно перейти до змінної х, тобто підставити замість у вираз
необхідно перейти до змінної х, тобто підставити замість у вираз 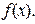 .
.
8.7. Похідні обернених тригонометричних функцій.
За допомогою теоремою 8.11 отримаємо формули для похідних від обернених тригонометричних функцій.
Теорема 8.12. Якщо 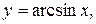 , то
, то
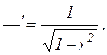 .
.
Доведення. Використаємо формулу (8.3). У нас прямою функцією 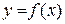 є функція
є функція 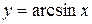 , а оберненою до неї
, а оберненою до неї 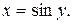 . Тому
. Тому
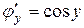 і
і 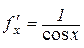
або, якщо перейти до змінної х,
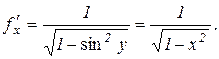 .
.
Таким чином,
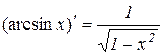
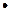
Теорема 8.13. Якщо 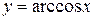 , то
, то
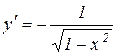 .
.
Доведення. Аналогічно попередній теоремі маємо
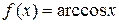 і
і 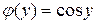 ,
,
тому
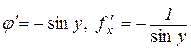
або
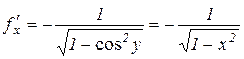 .
.
Тобто
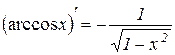
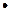
Теорема 8.14. Якщо  , то
, то
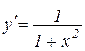 .
.
Доведення. Оберненою до функції 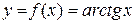 є функція
є функція 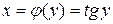 . Тому
. Тому 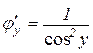 і за формулою (8.3) отримуємо
і за формулою (8.3) отримуємо 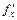
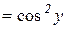 або, якщо перейти до змінної х,
або, якщо перейти до змінної х,
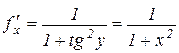
Теорема 8.15. Якщо 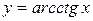 , то
, то
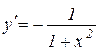 .
.
Доведення. Аналогічно попередній теоремі маємо
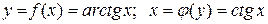 ;
;
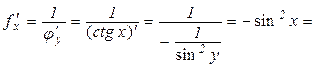
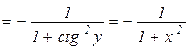 .
.
Приклад 8.7. Знайти похідну функції 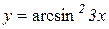 .
.
Розв’язування:
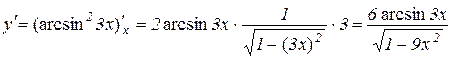 .
.
Тут використали теорему про похідну від складної функції: спочатку беремо похідну від степеневої функції u2, де u=arcsin3x, далі від оберненої тригонометричної – 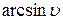 , де
, де 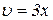 , і в кінці – від 3х.
, і в кінці – від 3х.
Приклад 8.8. Знайти похідну функції 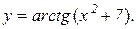 .
.
Розв’язування.
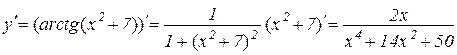 .
.
8.8. Таблиця похідних.
Всі отримані формули диференціювання зведемо в одну таблицю.
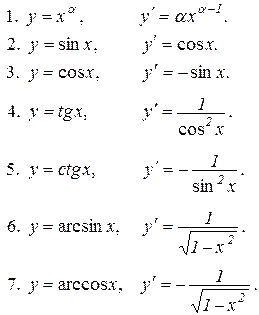
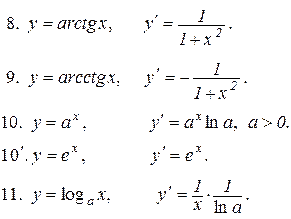
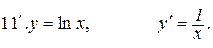
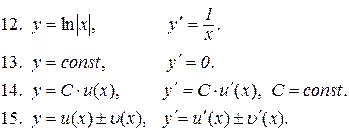
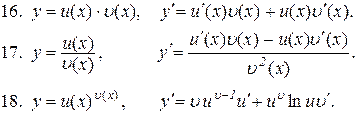
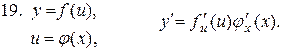
8.9. Похідна функції, заданої параметрично.
Розглянемо два рівняння
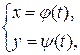 (8.5)
(8.5)
де t набуває значення на відрізку [t0, t1]. Кожному значенню аргументу t відповідають конкретні значення змінних х і у. Змінюючи t, будемо отримувати різні пари (х, у), сукупність яких можна розглядати як таблично задану функцію у з аргументом х. Якщо ж функція 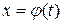 має обернену функцію
має обернену функцію 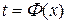 , то після підстановки останньої в функцію
, то після підстановки останньої в функцію 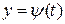 отримаємо функцію (8.5) в явному вигляді
отримаємо функцію (8.5) в явному вигляді 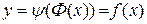 .
.
 Таким чином, пару функцій (8.5) можна розглядати як функцію у аргументу х за допомогою проміжного аргументу t, який ми називатимемо параметром, а саму функцію – параметрично заданою функцією.
Таким чином, пару функцій (8.5) можна розглядати як функцію у аргументу х за допомогою проміжного аргументу t, який ми називатимемо параметром, а саму функцію – параметрично заданою функцією.
Наведемо кілька прикладів параметрично заданих функцій.
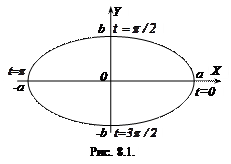
Приклад 8.9. Еліпс. Розглянемо рівняння
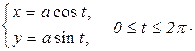 (8.6)
(8.6)
Ця система рівнянь задає в декартовій прямокутній системі координат ОХУ лінію, яка називається еліпсом (рис. 8.1).
|
|
|
Функцію (8.6) можна перевести в функцію, задану неявно. Дійсно, якщо перше рівняння розділити на а, а друге – на b; отримані рівняння піднести до квадрату і скласти, то дістанемо
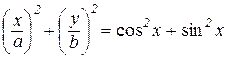
або
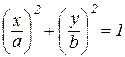 .
.
Остання формула є канонічним рівнянням еліпса з центром у початку координат і півосями а і b. Таким чином, система (8.6) є параметричним заданням еліпса.
Приклад 8.10. Циклоїда.
Означення. 8.1 Циклоїдою називається лінія, яка описується точкою, що лежить на колі, яке котиться без ковзання по прямій (рис. 8.2).
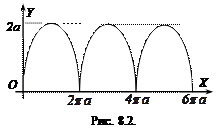 Цю криву можна описати системою рівнянь:
Цю криву можна описати системою рівнянь:
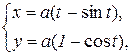
де а – радіус кола.
Значення параметра t в точках на осі ОХ дорівнює 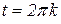 , де
, де 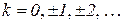
Перейдемо до обчислення похідної від функції заданої параметрично. Нехай 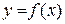 задана системою (8.5). Припустимо, що для функцій
задана системою (8.5). Припустимо, що для функцій 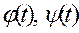 існує похідна по змінній t і функція
існує похідна по змінній t і функція 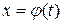 має обернену функцію
має обернену функцію 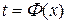 , яка також має похідну, але по змінній х. Тоді задану параметрично функцію можна розглядати як складну функцію
, яка також має похідну, але по змінній х. Тоді задану параметрично функцію можна розглядати як складну функцію 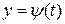 ,
, 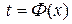 . Змінна t грає роль проміжного аргументу.
. Змінна t грає роль проміжного аргументу.
За теоремою 8.7 отримуємо
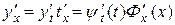 .
.
Але за теоремою 8.11 виходить, що 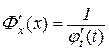 , і, таким чином,
, і, таким чином,
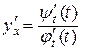 або
або 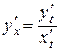 .
.
Остання формула дає змогу обчислювати похідну функції, заданої параметрично, не переводячи її в неявно або явно заданий вигляд.
Приклад 8.11. Знайти похідну функції
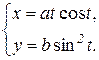
Розв’язування.
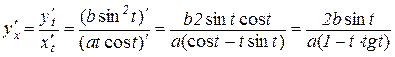 .
.
Приклад 8.12. Знайти значення похідної для функції
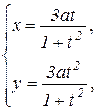
при t=2.
Розв’язування. Спочатку знайдемо похідну 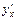 в загальному вигляді
в загальному вигляді
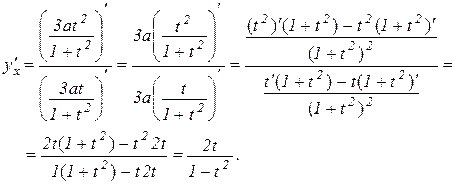
Тепер знайдемо значення останнього виразу при t=2:
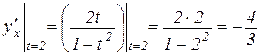 .
.
Запитання для самоконтролю.
1. Виведіть формули для похідних функцій 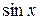 ,
, 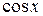 .
.
2. Виведіть формули для похідних функцій 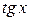 ,
, 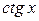 .
.
3. Чому дорівнює похідна від логарифмічної функції 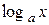 ?
?
4. Як співвідносяться похідні функцій 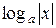 і
і 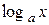 ?
?
5. Яка функція називається складною?
6. Виведіть правило диференціювання складної функції.
7. Як обчислюється похідна функції, заданої неявно?
8. Сформулюйте і виведіть теорему про похідну від степеневої функції.
9. Як обчислюється похідна показникової функції?
10. Запишіть формулу для похідної функції 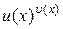 .
.
11. Сформулюйте поняття оберненої функції. В якому випадку вона існує?
12.Виведіть правило диференціювання оберненої функції.
13. Чому рівні похідні від обернених тригонометричних функцій?
14. Запишіть таблицю похідних.
15. Наведіть приклади параметрично заданої функцій.
16. Як диференціюється функція задана параметрично?
Приклади до розділу 8.
1. Знайти похідну функції:
а) 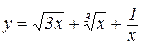 . Відп.:
. Відп.: 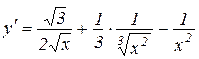 .
.
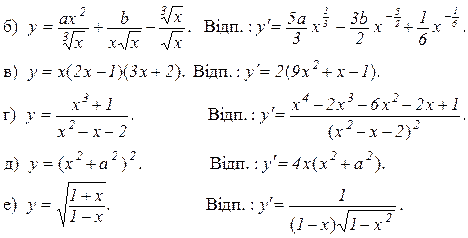
2. Знайти похідну функції:
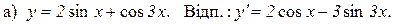
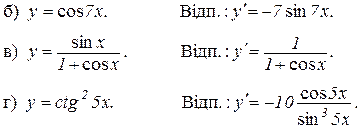


3. Продиференціювати функції:
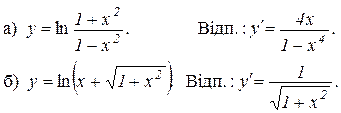
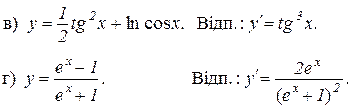
4. Продиференціювати функції:
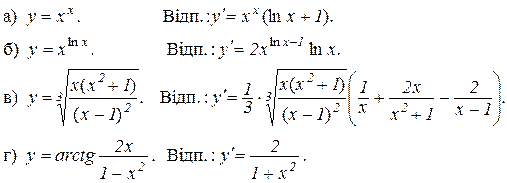
5. Знайти похідні функцій, заданих неявно і параметрично:
а) 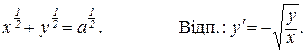
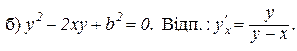
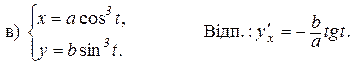

|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 893; Нарушение авторских прав?; Мы поможем в написании вашей работы!