Локально-интерполяционные (составные) квадратурные формулы

Многочлен Якоби определяется формулой

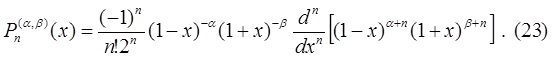
Многочлены Якоби (23) ортогональны на отрезке 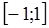с весом 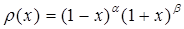и для любого многочлена 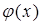степени меньшей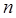

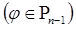
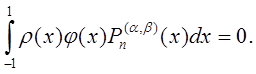
С помощью теоремы 3 получаем, что алгебраический порядок точности квадратурной формулы (22) равен .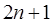

Квадратурная формула (22) содержит два параметра 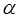и 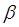, из нее могут быть получены специализированные квадратурные формулы, соответствующие распространенным видам степенных особенностей (см. [3]). В справочниках приведены квадратурные формулы Гаусса с другими весами.

Для повышения точности квадратурных формул используют прием, идея которого восходит к римановым интегральным суммам. Отрезок интегрирования 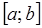разбивают на некоторое число частичных отрезков, на каждом из которых применяют квадратурную формулу с небольшим числом узлов. В качестве параметра квадратурного процесса теперь используют число частичных отрезков.

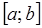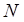Разобьем отрезок на частичных отрезков точками 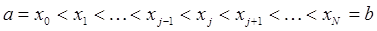. Для вычисления интеграла на каждом частичном отрезке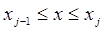 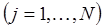применим интерполяционную квадратурную формулу с 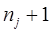узлам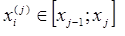и и

коэффициентами 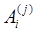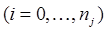. Получим квадратурную формулу

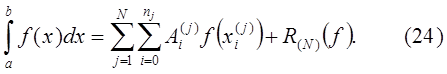
Пусть 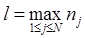и 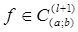, тогда для погрешности квадратурной формулы (24) имеет место оценка

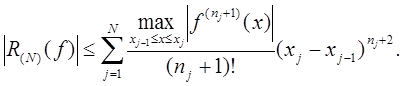
Квадратурная формула (24) называется локально-интерполяционной или составной.

Наиболее часто формула (24) используется в случае, когда отрезок 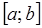разбит на частичные отрезки равной длины 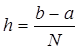и на каждом частичном отрезке используется квадратурная формула Ньютона-Котеса с 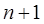узлами. Из (24) получаем пр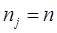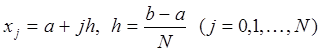и , и 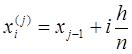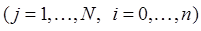локально-интерполяционную квадратурную формулу

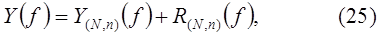
где

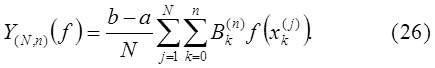
Сумма абсолютных величин коэффициентов формулы (26)

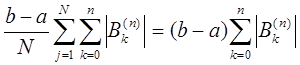
не зависит от числа частичных отрезков .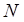

Оценка погрешности квадратурной формулы (25) имеет вид

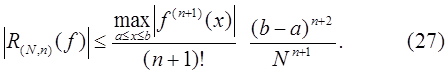
Из теоремы 2 и (27) следует, что квадратурный процесс, порожденный локально-интерполяционной квадратурной формулой (25), является сходящимся при 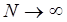(со скоростью 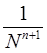на функциях из класса ).

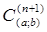Приведем простейшие составные квадратурные формулы, часто применяемые в практике.

Дата добавления: 2014-11-18