Элементы статистической обработки данных 11 страница

Дисперсия случайной величины X характеризует разброс (рассеяние, распределение) ее отсчетов на числовой оси относительно математического ожидания m_x этой случайной величины. Обозначают дисперсию случайной величины X как D[X] или как D_x.

Пусть математическое ожидание m_x случайной величины X задано. Тогда дисперсия случайной величины вычисляется так:

D[X]=M[X²]-(m_x)², (8.8)

а именно, дисперсия СВ равна разности между ее средним квадратом и квадратом ее среднего.

Центрированной случайной величиной X_Ц, соответствующей X, называется отклонение X от ее математического ожидания m_x:

X_Ц=X-m_x.

Геометрически переход от X к X_Ц означает перенос начала координат на числовой оси в точку m_x. Иногда удобнее бывает вычислять дисперсию по формуле

D[X]=D_x=M[(X-m_x)²=M[(X_Ц)²], (8.9)

то есть дисперсией случайной величины X называют математическое ожидание квадрата соответствующей ей центрированной случайной величины X_Ц.

Отметим существенный факт. Если размерность математического ожидания m_x совпадает с размерностью самой случайной величины X, то дисперсия имеет размерность квадрата размерности случайной величины. Удобнее было бы оперировать с числовыми характеристиками одной размерности. Для этого из дисперсии извлекают корень квадратный. Полученную величину называют средним квадратическим отклонением СКО случайной величины X и обозначают как s_x:

s_x= 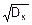. (8.10)

Размерность СКО совпадает с размерностью случайной величины.

Рассмотрим числовые характеристики дискретных случайных величин.

МО дискретной случайной величины вычисляют так:

M[X]=m_x=x₀´p₀+x₁´p₁+¼+x_n´p_n=

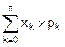= . (8.11)

Как видим, математическое ожидание дискретной случайной величины – это взвешенная сумма ее отсчетов, когда каждый отсчет x_k умножается на свою вероятность p_k (на свой вес), и полученные произведения суммируются.

Дисперсия дискретной СВ по формуле (8.8) вычисляется так:

D_x= 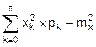. (8.12)

Таблица 8.2
qk
pk	0.2	0.3	0.4	0.1
Таблица 8.3
rk	-3
pk	0.2	0.5	0.2	0.1

Пример. В табл. 8.2 и 8.3 заданы законы распределения дискретных величин Q и R, соответственно. Найдем числовые характеристики этих случайных величин.

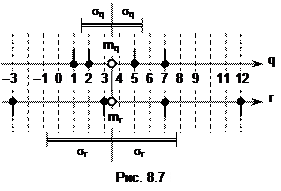
На рис. 8.7 показано размещение отсчетов случайных величин Q и R на числовой прямой. Сначала по формуле (8.11) вычисляем математические ожидания для случайных величин Q и R:

m_q=1´0.2+2´0.3+5´0.4+7´0.1=3.5 (см. рис. 8.7),

m_r=-3´0.2+3´0.5+7´0.2+12´0.1=3.5 (см. рис. 8.7).

Как оказалось, Q и R имеют одинаковые средние: m_q=m_r=3.5. Но легко заметить (рис. 8.7), что отсчеты R относительно m_r разбросаны сильнее, чем отсчеты Q относительно m_q.

По формулам (8.12) и (8.10) вычислим дисперсии и СКО для случайных величин Q и R:

D_q=1²´0.2+2²´0.3+5²´0.4+7²´0.1-3.5²=4.05,

s_q=2.01 (рис. 8.7),

D_r=(-3)²´0.2+3²´0.5+7²´0.2+12²´0.1-3.5²=18.25,

s_r=4.27 (рис. 8.7).

Как видим, большему разбросу отсчетов случайной величины отвечают большие дисперсия и СКО.

Пример. Найти числовые характеристики дискретной случайной величины Z (табл. 8.1).

Действуя по формуле (8.11), находим МО для дискретной СВ Z:

M[z]=m_z=0´0.064+1´0.288+2´0.432+3´0.216=1.8.

Значит, центром тяжести для точек z={0, 1, 2, 3} из (табл. 8.1) будет точка m_z=1.8.

Действуем по формулам (8.8) и (8.10):

D_z=0²´0.064+1²´0.288+2²´0.432+3²´0.216-1.8²=0.72.

s_z=0.85.

Рассмотрим числовые характеристики непрерывных случайных величин.

Формулу для математического ожидания непрерывной случайной величины получим, если в соотношении (8.11) выполним такие замены:

ü отсчеты x_k на переменную x,

ü вероятность p_k на элемент вероятности f(x)´dx,

ü сумму n слагаемых – на интеграл в бесконечных пределах:

M[X]= 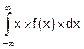. (8.13)

Дисперсия непрерывной случайной величины вычисляют так:

D_x= 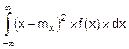. (8.14)

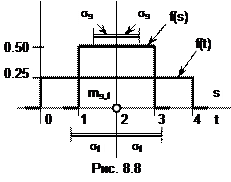
Пример. Случайные величины S и T заданы своими плотностями распределения (рис. 8.8):

f(s)= 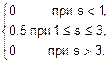f(t)=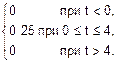

Плотности распределения f(s) и f(t) отвечают свойству 2: площадь под каждой из них равна единице.

Найдем числовые характеристики случайных величин S и T.

По формуле (8.13) вычисляем математические ожидания:

m_s= 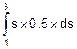= =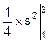2 (см. рис. 8.8),

m_t= 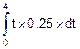= =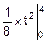2 (см. рис. 8.8).

А теперь для S и T вычисляем дисперсии по формуле (8.14) и СКО по формуле (8.10):

D_s= = = ,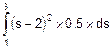

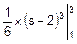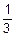s_s= 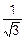=0.58 (рис. 8.8),

D_t= = = ,

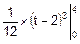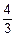s_t= =1.15 (рис. 8.8).

И в этом случае случайная величина, значения которой занимают на числовой оси более широкую зону, имеет большие дисперсию и СКО.

Пример. Вычислить МО, дисперсию и СКО случайной величины W, распределенной по закону (8.4).

Вычисляем m_w по формуле(8.13). При этом учитываем, что заданная f(w)=0 при w<0 нижний предел интеграла равен 0.

m_w= .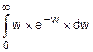

Этап 1. F(w)= = =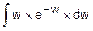

= =

= .

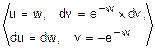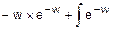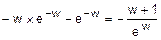Этап 2. m_w= 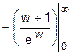= =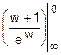1- =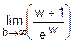

=1- 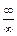!=áГл. 6, правило Лопиталяñ=

=1- 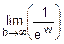=1-0=1.

При вычислении D_w действуем по формуле (8.14), в которой нижний предел интеграла равен 0.

D_w= .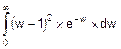

Этап 1. F(w)= =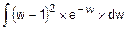

= =

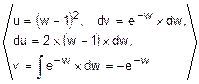=-(w-1)²´e^-w+2´ =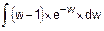

= =

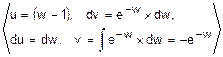=-(w-1)²´e^-w+2´ =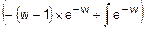

=-(w-1)²´e^-w+2´(-(w-1)´e^-w-e^-w)=

= = .

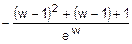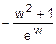Этап 2. D_w= = =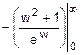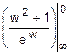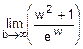

=1- 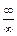=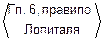1- != =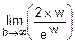

=1- =1- != =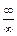

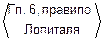=1- 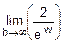=1-0=1.

s_w=1.

8.4. Канонические распределения случайных величин

В теории вероятностей оперируют с большим количеством распределений случайных величин. Многие из них считаются каноническими. Мы изучим одно из канонических распределений для дискретных случайных величин и одно – для непрерывных.

Биномиальное распределение. Пусть выполняется серия из n опытов. В каждом опыте с вероятностью p=const происходит (а с вероятностью q=1-p не происходит) событие A. Опыт считается удачным, если в этом опыте событие A случилось. Количество удачных опытов в такой серии есть случайная дискретная величина X. Она может принимать целые неотрицательные значения X={0, 1, 2, 3,¼, n}. Вероятность того, что событие A произойдет в серии из n опытов ровно m раз, то есть X примет значение, равное m, вычисляется по формуле Бернулли:

P(X=m)= 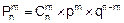. (8.15)

Тогда дискретная случайная величина X распределена по биномиальному закону с параметрами n и p. Исследуем, как ведет себя функция (8.15) при p=const и n=var.

На рис. 8.9 показаны графики биномиального распределения с параметрами: n={3, 8, 13}=var, p=0.6=const.

Ломаная 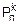называется многоугольником распределения. Многоугольник распределения – еще один способ задать закон распределения дискретной случайной величины.

Первый многоугольник на рис. 8.9 (с круглыми маркерами) представляет собою биномиальный закон распределения случайной величины Z (табл. 8.1). Параметры этого распределения n=3, p=0.6.

Математическое ожидание, дисперсию и СКО для случайной величины X, распределенной по биномиальному закону, вычисляют по формулам:

m_x=n´p, D_x=n´p´q=m_x´q, s_x= .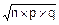

Пример. Найдем числовые характеристики случайных величин на рис. 8.9:

m_n=3=3´0.6=1.8,

D_n=3=1.8´0.4=0.72, s_n=3= 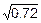=0.85.

m_n=8=8´0.6=4.8,

D_n=6=4.8´0.4=1.92, s_n=6= 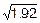=1.39.

m_n=13=13´0.6=7.8,

D_n=13=7.8´0.4=3.12, s_n=13= 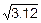=1.77.

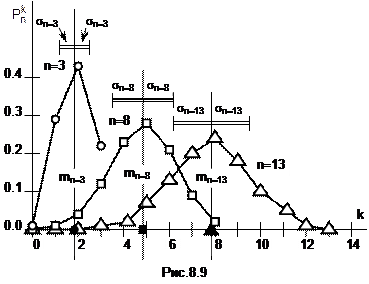
Полученные значения МО нанесены на ось 0k (рис. 8.9). При этом маркеры на многоугольнике распределения случайной величины и ее математического ожидания совпадают, только маркер МО черный. Здесь же отрезками показаны СКО для каждой СВ.

Как видим, при увеличении n многоугольники биномиального распределения смещаются вправо, и чем больше n, тем все более симметричной и плавной становится ломаная 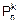. При этом максимумы многоугольников распределения уменьшаются, поскольку 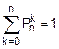. Значения МО близки к абсциссам максимумов многоугольников распределения. А с ростом n растет и СКО (рассеяние отсчетов СВ относительно ее МО).

Нормальное распределение. Непрерывная случайная величина X подчинена нормальному закону, если плотность ее вероятности описывается соотношением:

f(x)= 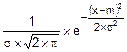. (8.16)

Параметры нормального распределения m и s не что иное, как числовые характеристики случайной величины X: m – ее математическое ожидание, s² –дисперсия X, а s – ее СКО.

По определению (8.5) функция нормального распределения имеет вид:

F(x)= 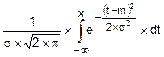. (8.17)

Плотность вероятности (8.16) не имеет первообразной в аналитической форме (говорят, что интеграл (8.17) не берется, то есть не выражается в элементарных функциях). В математике разработаны эффективные алгоритмы табличного представления функции нормального распределения. Правда, таблицы строились для нормированных параметров нормального распределения: m=0 и s=1. В былые времена такие таблицы имелись во всех учебниках и справочниках по теории вероятностей и математической статистике. Их использование для решения конкретных задач с размерными x, m, s требовало от исполнителей чрезмерных затрат труда и времени.

Сегодня эти алгоритмы реализованы в системах компьютерной математики. Так, в Mathcad формула (8.16) представлена встроенной функцией dnorm(x,m,s), а формула (8.17) – встроенной функцией pnorm(x,m,s). При использовании этих функций нет нужды нормировать исходные данные решаемой задачи.

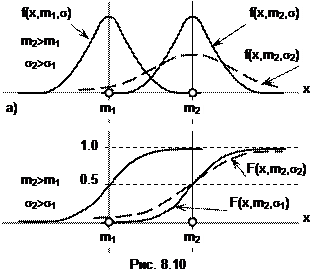
Плотность вероятности (8.16) и закон распределения (8.17) нормально распределенной СВ – функции двух параметров: ее МО m и ее СКО s. На рис. 8.10 приведены графики плотности вероятности f(x) (рис. 8.10,а) и функции распределения F(x) (рис. 8.10,б) нормально распределенной СВ. Как видим, увеличение математического ожидания m при постоянном СКО s приводит к смещению кривых f(x) и F(x) вправо вдоль оси абсцисс. А большему значению s при одном и том же m отвечают более пологие кривые f(x) и F(x) (с большим разбросом значений X).

В отношении нормально распределенной случайной величины X действует «правило трех сигм»:

отсчеты нормально распределенной случайной величины X практически не отклоняются от ее математического ожидания m на расстояние больше трех СКО s.

Дело в том, что

P(m-3´s<X<m+3´s)=0.997@1.

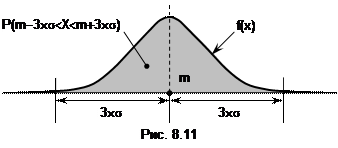
«Правило трех сигм» для нормального распределения с параметрами m и s иллюстрирует рис. 8.11. Заштрихованная площадь под кривой f(x) (вероятность попадания значений СВ X в диапазон от m-3´s до m+3´s), равна 0.997. Значит, событие (m-3´s<X<m+3´s) практически достоверное. А вероятность выхода ее значений за пределы этого диапазона равна незаштрихованной площади под кривой f(x) составляет 1-0.997=0.003. Значит, событие ù(m-3´s<X<m+3´s) практически невозможное.

Пример. Докажем «правило трех сигм» для нормированных параметров нормального распределения m=0 и s=1. (А пронормировать можно любые параметры конкретной нормально распределенной случайной величины). Имеем:

f(x)= .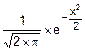

По определению

P(-3<X<+3)= =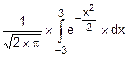

=áсвойство 4 определенных интеграловñ=

=2´ =2´J.

Интеграл

J=

вычисляем методом Рунге-Ромберга по формуле трапеций, поскольку f(x) первообразной не имеет, то есть формулу Ньютона-Лейбница для вычисления J применить нельзя.

1. Строим таблицу f(x) с шагом h.

n=4. h= =0.75. xt₀=a=0, xt_i+1=xt_i+h, i= .

yt_i=f(xt_i), i= .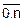

Вычисляем значение J по формуле трапеций на шаге h.

i
xti	0.00	0.75	1.50	2.25	3.00
yti	0.39894	0.30114	0.12952	0.03174	0.00443
j

F_h= 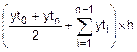=0.49806.

3. Формируем таблицу с шагом 2´h:

n2= 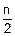=2, h2=2´h, yt2_j, j= .

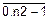Вычисляем значение J по формуле трапеций на шаге 2´h:

F_2h= 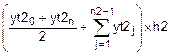=0.49681.

3. Вычисляем поправку Рунге:

PR= 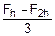=0.00042.

4. Вычисляем значение J по формуле Рунге-Ромберга:

J=F_RR=F_h+PR=0.49848.

Таким образом, искомая вероятность попадания значений нормально распределенной нормированной СВ в интервал ]-3,+3[ равна

P(-3<X<+3)=2´J=0.99696.

На практике «правило трех сигм» позволяет оценить СКО любой случайной величины, которую можно считать распределенной по нормальному закону. Например, по результатам пристрелки оружия фиксируют максимальное отклонение точки попадания от центра мишени. Третья часть этого отклонения и будет оценкой СКО – кучностью стрельбы.

8.5. Энтропия и информация

Во второй половине XX века человечество вступило в новую стадию своего цивилизационного развития, которая названа информационным обществом. В нашей стране разработана "Стратегия развития информационного общества в Российской Федерации" (утв. Президентом РФ 07.02.2008 N Пр-212). Основные черты информационного общества в стратегии определены так.

Информационное общество характеризуется высоким уровнем развития информационных и телекоммуникационных технологий и их интенсивным использованием гражданами, бизнесом и органами государственной власти.

Увеличение добавленной стоимости в экономике происходит сегодня в значительной мере за счет интеллектуальной деятельности, повышения технологического уровня производства и распространения современных информационных и телекоммуникационных технологий.

Существующие хозяйственные системы интегрируются в экономику знаний. Переход от индустриального к постиндустриальному обществу существенно усиливает роль интеллектуальных факторов производства.

Международный опыт показывает, что высокие технологии, в том числе информационные и телекоммуникационные, уже стали локомотивом социально-экономического развития многих стран мира, а обеспечение гарантированного свободного доступа граждан к информации – одной из важнейших задач государств.

Информационные технологии представляют собой организованное научно-методическое обеспечение переработки информации.

Переработка информации – это совокупность таких информационных процессов:

производство информации:генерация, включая моделирование; рецепция, измерение,

интерпретация информации: преобразование, логическая обработка, аккумуляция,

коммуникация информации: передача, хранение, представление.

Информация, как видим, является предметом и продуктом информационных технологий.

Юридическая деятельность осуществляется в сфере социальных систем и явлений, то есть в сфере отношений между людьми. Поэтому в этой сфере естественно использовать тот смысл термина «информация», который определен ст. 2 Федерального Закона "Об информации, информационных технологиях и о защите информации":

информация – сведения(сообщения, данные) независимо от формы их представления.

В сфере юриспруденции применяются две формы представления информации.

Вербальная (словесная) форма, когда сведения задаются устной или письменной речью. Она используется для качественной характеристики объектов и процессов. Такая форма фиксации и передачи информации принята в большинстве правовых актов.

Числовая форма (форма данных), когда сведения задаются количественными характеристиками объектов и процессов. А эти характеристики получены путем наблюдений, измерений, путем обработки их результатов с использованием математических методов.

Современные информационные технологии реализуются на компьютерах. И вся информация в компьютерах представлена в числовой форме, а именно, двоичными кодами. Следовательно, числовая форма представления информации является универсальной.

Отметим, что каждый из двух первых информационных процессов (производство и интерпретация информации) начинаются и завершаются третьим, а именно, коммуникацией информации. Коммуникация информации – это передача ее в пространстве по каналам связи или во времени посредством хранения на носителях. При передаче информации в пространстве стремятся минимизировать время передачи, а при передаче ее во времени минимизируют пространство (объем носителя).

Главная задача системы коммутации (рис. 8.12) состоит в том, чтобы в достаточной мере обеспечить взаимно-однозначное соответствие между информационными массивами ИМ на ее входе и на ее выходе. Нарушение этого соответствия обусловлено неизбежными помехами той или иной природы, которые воздействуют на систему коммутации. Этим определяется вероятностный характер процессов в системе коммутации. Вероятностный характер имеет и процесс формирования входного ИМ. Случайным событием здесь является получение того или иного элемента входного массива. Точно так, и получение выходного ИМ носит вероятностный характер, а случайное событие – появление того или иного элемента выходного ИМ.

Рассмотрим некоторое конечное множество X случайных событий x₁,x₂,…,x_N. Любые действия, приводящие к наступлению события x_i, i= 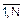, называют, как мы уже знаем, опытом или испытанием, а сам ансамбль x₁,x₂,…,x_N называют пространством элементарных событий W. Получение информации в опыте связано с тем, что до его осуществления имеется известная неопределенность в его исходе. Известен полный набор возможных исходов испытания W, но какой именно исход наступит в результате опыта, сказать нельзя. По окончании испытания наступает одно из N событий. Тем самым неопределенность относительно результатов опыта уменьшается. Это уменьшение неопределенности относительно результатов испытания после его осуществления и понимают как получение информации. Обозначим количественную меру неопределенности до опыта как H_ДО, а количественную меру оставшейся после опыта неопределенности как H_ПО. Тогда количественной мерой информации I(X) в опытах с множеством X будет разность

Таблица 8.4
i	xi	p(xi)
	x1	p(x1)
	x2	p(x2)
¼	¼	¼
N	xN	p(xN)

I(X)=H_ДО-H_ПО. (8.18)

Обычно множество X задают рядом распределения (табл. 8.4). Здесь p(x_i) – вероятность наступления события x_i. Эти вероятности отвечают условию

p(x₁)+p(x₂)+¼+p(x_N)=1. (8.19)

Количественной мерой неопределенно-сти в опытах с конечным множеством случайных событий X является величина H(X), которая называется энтропией:

H(X)=-(p(x₁)´log_a(p(x₁))+p(x₂)´log_a(p(x₂))+¼+

+p(x_N)´log_a(p(x_N)))=

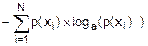= . (8.20)

Формула (8.20) выведена К. Шенноном в 1948 г. Поясним ее смысл. Для этого перепишем ее так:

H(X)= .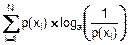

Величину H_i= 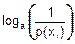можно назвать собственной неопределенностью случайного события x_i. Тогда величина

H(X)= =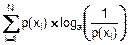

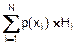
представляет собою математическое ожидание для H_i или среднюю неопределенность исходов опыта с множеством X случайных событий.

В опытах с множеством случайных событий X имеем

H_ДО=H(X).

Результатом опыта является исход x_i и только он. Такой исход является достоверным, действительно наступившим в опыте. Это значит, что при наступлении достоверного исхода неопределенность отсутствует, то есть

H_ПО=0,

и количество информации, полученное в таком испытании

I(X)=H(X).

Опыты описанной категории описывают процессы производства и интерпретации информации.

Перечислим свойства энтропии.

1. Энтропия равна нулю, если в любом опыте с множеством X исход известен заранее: всегда наступает событие x_j и никогда не происходят события x_i, то есть вероятность p_j=1, а все вероятности p_i, i¹j равны нулю. Неопределенность в таком опыте отсутствует. А отсутствие неопределенности означает, что энтропия равна нулю.

Дата добавления: 2014-11-18