Понятие непрерывности функции

Рассмотрим функцию y=f (x), определенную в точке x ₀ и в некоторой ее окрестности.

Определение 1. Функция f (x) называется непрерывной в точке x ₀, если

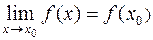. (1)

Так как , то соотношение (1) можно записать в следующем виде:

,

т.е. для непрерывной функции можно знак предела вносить под знак функции.

Дадим еще одно определение непрерывности равносильное определению 1. Для этого в равенстве (1) перенесем f (x ₀)в левую часть и внесем под знак преде-

ла. Так как условия x 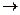x ₀ и (x – x ₀) 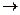0 равносильны, то получаем:

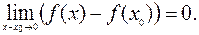(2)

Разность x – x ₀называется приращением аргумента x в точке x ₀и обозначается Δ x, а разность f (x) – f (x ₀) – приращением функции и обозначается Δ y. В этих обозначениях равенство (2) принимает вид:

. (3)

Это соотношение и есть еще одно определение непрерывности, которое можно сформулировать так:

Определение 2. Функция f (x) называется непрерывной в точке x ₀, если ее приращение Δ y=o (1) при Δ x 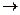0.

Пример. Докажем непрерывность y= sin x в произвольной точке x ₀.

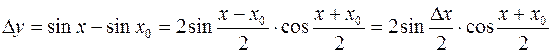
Полученное выражение есть произведение ограниченной функции 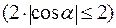на бесконечно малую (в силу леммы 2 §10 при Δ x 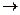0). По одному из свойств б.м. функций получаем Δ y=o (1) при Δ x 0,что и доказывает непрерывность y= sin x в произвольной точке x ₀.

Определение 3. Функция f (x)называется непрерывной в точке x ₀слева (справа), если

.

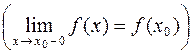Например, функция y= [ x ] непрерывна справа в любой целой точке, т.к. [ k+ 0] = [ k ] =k, в то же время слева она не является непрерывной [ k– 0] =k– 1 ≠ [ k ].

Из общих теорем о пределах функций легко получить такие результаты.

Теорема 1. Функция f (x)непрерывна в точке x ₀тогда и только тогда, когда она непрерывна в этой точке, как справа, так и слева, т.е.

f (x ₀ + 0)= f (x ₀ – 0)= f (x ₀)

Теорема 2. Пусть функции f (x)и g(x) непрерывны в точке x ₀, а функция F (u) непрерывна в точке u₀ =f (x ₀). Тогда и функции f (x)±g(x), f (x)·g (x), f (x): g(x)(при условии g(x ₀)≠0) и F (f (x))непрерывны в точке x ₀.

Если бы мы могли доказать непрерывность всех основных элементарных функций (как мы это сделали для синуса), то из теоремы 2 мы получили бы еще один важный результат.

Теорема 3. Всякая элементарная функция непрерывна в любой точке ее области определения (входящей в эту область с некоторой окрестностью).

Определение 4. Говорят, что функция f (x)непрерывна на промежутке 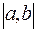, если она непрерывна в любой точке промежутка (в граничных точках промежутка подразумевается одностороння непрерывность).

§13. Классификация точек разрыва

I Определение

Точка x ₀называется точкой разрыва функции f (x),если эта функция не является непрерывной в точке x ₀.

Определение непрерывности, т.е. равенство , подра-зумевает следующие три условия:

1) x ₀ Î D (y);

2) существует и конечен;

3) .

При нарушении хотя бы одного из этих условий точка x ₀ и будет точкой разрыва. К точкам разрыва относят и те точки, не принадлежащие области определения функции, в окрестности (хотя бы односторонней) которых функция определена. Примером служит точка x ₀ = 0для функций и y= ln x.

II Точка устранимого разрыва

Точка x ₀называется точкой устранимого разрыва функции y=f (x), если , существует и конечен, но f (x ₀)≠ b или .

Например, функция

имеет в нуле устранимый разрыв, ибо , а f (0)=0≠1. Еще один пример дает функция 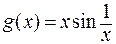, которая не определена в нуле, но существует и конечен.

III Точка разрыва 1^го рода

Точка x ₀ называется точкой разрыва 1^го рода функции f (x), если в этой точке

функция имеет конечные, но не равные друг другу односторонние пределы:

f (x ₀ + 0)≠ f (x ₀ – 0).

Сама точка x ₀ при этом может, как принадлежать, так и не принадлежать области D (y).

Разность f (x ₀ + 0) – f (x ₀ – 0) называется скачком функции в точке x ₀.

Примеры.

1) f (x)=sign x: f (0 + 0)=1, f (0 – 0)= –1.

2) f (x)=[ x ]: для любой целой точки f (k +0)= k, f (k –0)= k –1.

3) f (x)= : f .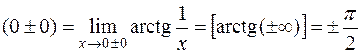

4) f (x)= 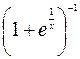(самостоятельно).

IV Точка разрыва 2^го рода

Точка x ₀ называется точкой разрыва 2^го рода функции y=f (x), если в этой точке, хотя бы один из односторонних пределов функции равен ±¥ или не существует.

Примеры. 5) Для f (x) = в примере 4 §9 получено: f (0+0)=+¥.

6) f (x) = 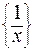в нуле не имеет предела, ибо для последовательности значений аргумента 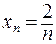, сходящейся к нулю, соответствующая последовательность значений функции не имеет предела.

7) См. пример 2 §9.

Замечание 1. При исследовании функции на непрерывность необходимо различать элементарные и неэлементарные функции. Например, – элементарная, следовательно, непрерывная всюду на D (y), а точки , не принадлежащие D (y), – это точки разрыва. Их тип устанавливается путем вычисления односторонних пределов. Функция же

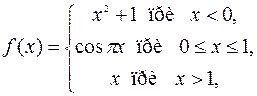
не является, вообще говоря, элементарной, поэтому может иметь разрыв в любой точке. Но каждое из трех выражений, определяющих функцию, есть элементарное, а значит, непрерывно. Эта функция может иметь разрывы только в точках, в которых переходит с одного выражения на другое. Итак, точки возможного разрыва

Замечание 2. Монотонная ограниченная функция может иметь разрывы только 1^го рода (следствие теоремы 12 §9).

Дата добавления: 2014-11-08