Формула интегрирования по частям в определенном интеграле

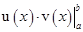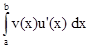= - (3.8)

Пример 2. Вычислить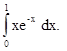

Решение. Прямому вычислению данного интеграла препятствует наличие сомножителя х в подынтегральном выражении. Поскольку производная от х ’=1, то целесообразно, используя (3.8) положить u = x. Тогда

=

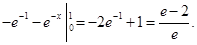
Замена переменной в определенном интеграле. Во многих случаях подынтегральное выражение можно упростить, если заметить, что его часть является дифференциалом некоторой функции. Тогда по аналогии с формулой (3.1) раздела 5 можно записать

= (3.9)

где x = j(t), j(a) = a, a=j^-1(a); j(b) = b, b = j^-1(b).

Пример 3. Вычислить .

Решение. Положив ln (х) = t, имеем d x / x = d t.

Если х = 1, то t = ln 1 = 0, если х = е, то t = ln е = 1. Тогда

Глава 5. Приложения определенного интеграла

1. Вычисление площади плоских фигур. Как уже отмечалось, если f (x) ³ 0 на отрезке [a,b], то определенный интеграл от функции численно равен площади криволинейной трапеции, ограниченной кривой y = f (x), осью абсцисс и прямыми x = a, и x = b.

(5.1)

Если на [a,b] функция, как показано на рис.5.1, меняет знак, то необходимо вычислить интеграл от модуля подинтегральной функции.

(5.2)

Это означает, что если на отрезке [а,с] Ì [a,b] функция f(x) < 0, то на этом отрезке берется отрицательное значение функции

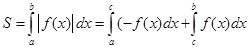
Рис. 5.1. Вычисление площади при помощи определенного интеграла

Пример 1. Вычислить площадь, ограниченную осью абсцисс и синусоидой на отрезке [0,2p].

Решение. Поскольку sin(x) ³ 0 на отрезке [0, p] и sin(x) £ 0 на [p,2p], то искомая площадь S равна

S = - (cosp - cos0) + (cos2p -

- cosp) = -(-1 -1) +(1 + 1) = 4.

В более общем, случае требуется вычислить площадь плоской фигуры ограниченной несколькими кривыми линиями. В этом случае искомая площадь есть алгебраическая сумма площадей нескольких криволинейных трапеций. Например, как показано на рис.5.2

Рис. 5.2. Вычисление площади плоской фигуры.

Пример 2. Вычислить площадь фигуры, ограниченной функциями y₁=½x - 2½ и y₂ = 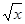(рис. 5.3).

Рис. 5.3.

Решение. Найдем точки пересечения линий. Для этого решим уравнение

y₁(х) = y₂(х)

Возведем в квадрат левую и правую часть

или ; .

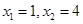Учтем, что .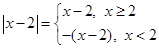

Следовательно

Вычисление длины дуги. Пусть некоторая гладкая плоская кривая описывается функцией f (x) и отрезку [a,b] оси абсцисс отвечает дуга AB. Произвольным образом разобьем эту дугу, как показано на рис.5.4 на n частей точками M₀, M₁,..., M_n. Получим элементарные дуги. Соединив каждые две соседние точки прямой, получим вписанную в дугу AB ломаную линию. Длину звена ломанной D l _i, лежащую между точками М_i M_i+1, где М_i(x_i, f(x_i)), М_i+1(x_i+1, f(x_i+1)) находим по формуле

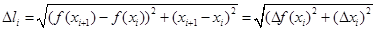
Длина элементарной дуги М_i M_i+1 примерно равна D l _i

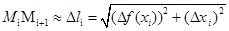. (5.3)

Просуммируем (5.3) по всем элементарным дугам, тогда длина L дуги АВ равна

Рис. 5.4. Длина дуги.

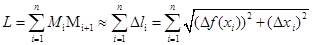
Выражение, стоящее в правой части равенства является интегральной суммой. При бесконечном увеличении числа точек разбиения 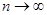, проводимого произвольным образом, если каждый раз длина самой большой элементарной дуги r будет стремится к нулю ,то длина ломаной будет неограниченно приближаться к длине дуги. Тогда длина дуги L плоской кривой

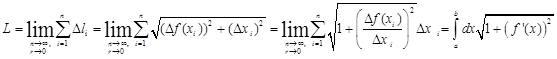(5.4)

Если кривая задана в параметрическом виде: х = j(t), y = y(t) (a£ t £b), то длина кривой вычисляется по формуле

(5.5)

Пример 1. Найти длину дуги кривой y ² = x ³ , заданной на отрезке от x = 0 до x = 1 (y ³ 0).

Решение. . Подставляя затем этот результат в (5.4), получим

Пример 2. Найти длину дуги кривой x = a cos³ t, y = a sin³ t, если t изменяется 0 до p/2.

Решение. Вначале находим производные по t

x ¢(t) = -3 a cos² t ּsin t, y ¢(t) = 3 a sin² t ּcos t

Подставляя в формулу (5.5), имеем

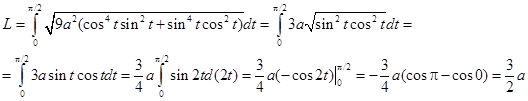
Вычисление объемов тел. Пусть дано тело переменного сечения, расположенной над осью ОХ (рис.5.5), ограниченное плоскостями х = а и х = b. Объем тела обозначим за V. Разделим отрезок [ a, b ] на произвольные n частей, при этом координаты точек деления удовлетворяют соотношению

x ₀ = a < x ₁ < x ₂ <... < x _{i -1}< x _i <... < x _n = b.

В точках деления проведем плоскости, перпендикулярные оси ОХ. Тело разделится на n узких слоев (элементарных объемов) шириной Δ x _i = x _i - x _i-1 (i = 1, 2…n). Объем каждого такого слоя обозначим как Δ V _i. На каждом промежутке [ x _i-1, x _i] выберем произвольную точку . Обозначим за S(x*_i) площадь поперечного сечения тела в этой точке. Тогда

(5.6)

Рис. 5.5. Объем тела переменного сечения.

Просуммируем (5.6) по всем i, получим интегральную сумму

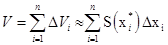(5.7)

Увеличим число разбиений n. При этом каждый раз обязательно должна уменьшатся длина наибольшего из разбиений Δ x _i, т.е. ранг дробления r должен стремится к нулю. Тогда объемтела переменного сечения V,будет равен пределу интегральной суммы при 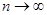и

(5.8)

Если тело получено при вращении криволинейной трапеции вокруг оси ОХ (рис. 5.6), то 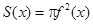. В этом случае объем тела V вычисляется по формуле

Рис. 5.6. Объем тела вращения.

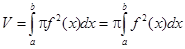(5.9)

Пример. Вычислить объем тела, полученного при вращении кривой y = sin(x) вокруг оси ОХ .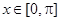

Дата добавления: 2014-11-18