Примеры решения для практики

Пример 1. .

Решение. Используем теорему: интеграл от разности функций равен разности интегралов.

Пример 2. Вычислить .

Решение. Сравним наш интеграл стабличным

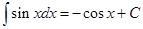
У нас , формально интеграл не табличный. Используем теорему о линейной замене переменной:

если 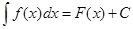, то .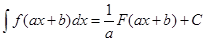

В интеграле , т.е. а = 2, следовательно

.

Проверим полученный результат дифференцированием

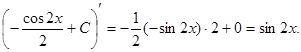
Интеграл взят правильно.

Пример 3. 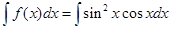, т.е. .

Решение. Так как , то используем теорему о «замене типа подведение под знак дифференциала»

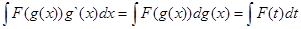, где t = g (x)

У нас . Тогда

Пример 4. , т.е. .

Решение. Так как , то то используем теорему о «замене типа подведение под знак дифференциала», . Тогда 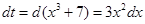. Домножим в числителе на 3, при этом надо и знаменатель умножить на 3.

.

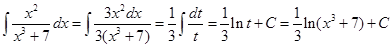Проверим дифференцированием

.

Пример 5. Найти .

Решение. Используем теорему о замене переменной

.

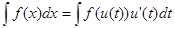Особенностью данного интеграла является то обстоятельство, что его подынтегральное выражение содержит множитель 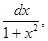который является дифференциалом функции arctg x. Поэтому в данном интеграле целесообразно ввести замену переменной: t = arctg x. Отсюда dt = d(arctg(x)) = 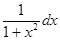и e^{arctg x} = e^t. Подставляя в исходный интеграл, имеем = e^{arctg x} + C.

Пример 6. Найти .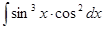

Решение. Здесь уместна замена t = cos x, т.к. dt = - sin x dx, и sin³x dx = sin²x sinx dx. Поэтому

Пример 7. Найти .

Решение. Используем метод интегрирования по частям

Так как производная от х равна 1, то возьмем u = x. Используем формулу, приведя схему записи удобную при использовании метода интегрирования по частям.

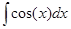= - x cosx + = - x cosx + sinx + C.

Пример 8. Найти .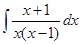

Используем метод разложения на простейшие. Знаменатель имеет два различных действительных корня, разложим подинтегральную функцию на простейшие слагаемые

Приравняем числители и учтем, что коэффициенты при одинаковых степенях х, стоящие слева и справа должны совпадать

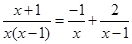
Следовательно

Пример 9. Найти .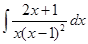

Используем метод разложения на простейшие. Знаменатель имеет действительные корни, причем корень -1 имеет кратность два. Разложим подинтегральную функцию на простейшие слагаемые

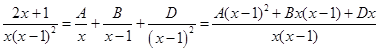
Приравняем числители и учтем, что коэффициенты при одинаковых степенях х, стоящие слева и справа должны совпадать

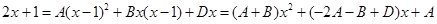
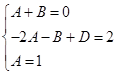
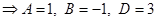
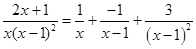
Следовательно

Пример 10. Найти .

Решение. Используем метод разложения на простейшие, разложим подинтегральную функцию на простейшие слагаемые

Приравняем числители

Так как коэффициенты при одинаковых степенях х, стоящие слева и справа должны совпадать, то .

.

Следовательно

Здесь использовано

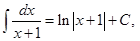
Пример 11. Найти .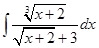

Сделаем замену переменной, позволяющую избавится от иррациональности

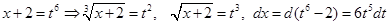
Под интегралом стоит неправильная дробь, поэтому разделим числитель на знаменатель и вычислим получившиеся интегралы

Под интегралом стоит неправильная дробь, поэтому разделим числитель на знаменатель и вычислим получившиеся интегралы

Пример 12. Вычислить площадь фигуры, ограниченной линиям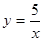и и .

Решение. Построим в системе координат эти линии. Найдем точки пересечения этих линий

Рис.1.

Обозначим эти точки через A и В. Итак, А(1; 5), В(5; 1). Искомая площадь S равна разности площадей фигур, ограниченных линиями , , 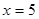, 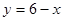(обозначим эту площадь через S₁) и линиями , , 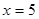, 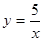(эту площадь обозначим через S₂). Таким образом

S = S₁ – S₂

Площадь S₂ может быть вычислена с применением определенного интеграла

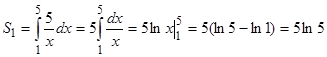ед ².

Площадь S₁ можно, конечно, вычислить как сумму площадей прямоугольного треугольника и прямоугольника, но удобнее все-таки вычислить S₁ как интеграл

.

Теперь можно вычислить и искомую площадь

S = S₁ – S₂ = 12 – 5 ln5

Ответ: S =12 – 5 ln5 ед ².

Пример 13. Вычислить объем тела, полученного вращением вокруг оси О фигуры, ограниченной прямой и параболой .

Найдем точки пересечения линий. Для этого решим уравнение . Получим .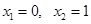

Рис. 2.

Объем тела может быть вычислен по формуле , где

, .

.

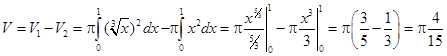Ответ: .

Раздел 7. Функции многих переменных. Ряды.

Глава 1. Функции двух переменных. Основные определения. Приращения функции.

Пусть на плоскости ХY задана область D. Каждой точке М этой области соответсвует упорядоченная пара чисел (х, у) - ее координаты.

Если каждой упорядоченной паре чисел (х, у) поставлено в соответствие по закону f число z, то говорят, что задана функция двух переменных

z = f (x, у) (1.1)

Область D называется областью определения функции. Множество Z ={z} образует область значений функции. График функции f (x, y) - поверхность в пространстве (рис 1.1), эту поверхность часто обозначают σ. Проекция поверхности σ на плоскость XOY и есть область D.

Рис.1.1. Функция двух переменных.

Функция двух переменных может быть также задана в виде таблиц.

Аналогично задается функция трех и более переменных. Физически, например, функцию трех переменных u = f (x, y, z,) можно интерпретировать как плотность вещества в объемной области D.

Следует заметить, что функции двух переменных являются самым простым и наглядным случаем среди всех функций многих переменных и поэтому обычно подробно рассматриваются. Полученные при этом свойства остаются верными и для функций произвольного числа переменных.

Если на оси Z нанести масштаб, и провести через точки деления плоскости, перпендикулярные оси Z, то поверхность σ разделится на части. На каждой линии сеченияповерхности σ плоскостью функция z = f (x, у) будет постоянной величиной. Линии сечения проектируют на плоскость ХY и называют линиями уровня (рис. 1.2).

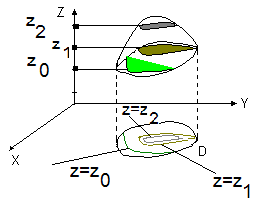
Рис. 1.2. Линии уровня.

Функция z = f (x, у) называется непрерывной в точке М₀(x ₀, y ₀), если имеет место равенство

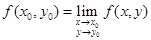
и точка М(x, y) стремится к М₀(x ₀, y ₀) оставаясь все время в области определения функции. Функция непрерывная в каждой точке области называется непрерывной во всей области.

Если функция непрерывна в ограниченной замкнутой области, то она достигает там своего наименьшего m и наибольшего M значений.

Приращения функции двух переменных. Выберем в области определения функции точку М₀ с координатами x ₀ и y ₀ т.е. М₀(x ₀, y ₀) и точку М₁ с координатами x ₁ и y ₁ М₁(x ₁, y ₁) (рис.3). вычислим в этих точках значения функции z ₀ = f(x ₀, у ₀) и z ₁ = f(x ₁, у ₁).

Рис. 1.3. Приращения функции двух переменных

Полным приращением функции двух переменных Δz называется разность ее значений в точках М₁ и М₀

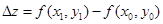. (1.2)

Сделаем дополнительное построение. Построим точку М₂(x ₁, y ₀) и М₃(x ₀, y ₁). Частным приращением по аргументу х Δ_хz называется разность значений функции в точках М₂ и М₀

, (1.3)

а частным приращением по аргументу у Δ_уz называется разность значений функции в точках М₃ и М₀

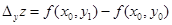. (1.4)

Сумма частных приращений, в общем случае, не совпадает с полным приращением.

Глава 2. Частные производные

Частной производной от функции двух переменных f (x, y) по переменной х при y = y ₀ называется предел, при Δ х стремящемся к нулю, отношения частного по х приращения функци 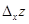к вызвавшему его приращению аргумента Δ х (если этот предел существует и конечен). Так как y₀ любое фиксированное число из области допустимых значений, то его можно заменить на просто у. Тогда

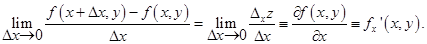
Частная производная от функции f (x, y) по переменной y определяется и обозначается аналогичным образом

То есть, при вычислении частной производной от функции двух переменных f (x, y) по х второй аргумент y выступает как величина постоянная. Если же вычисляется частная производная по y, то х принимается постоянной величиной.

Пример 1. Вычислить частные производные z_x¢ и z_y¢ от функции

f (x, y) = x ³ y ² + sin x - 4 y.

Решение. В соответствии с определением, имеем

f _x¢(x, y) = 3 x ² y ² + cos x и f _y¢(x, y) = 2 x ³ y - 4.

Частная производная от f (x, y) тоже является функцией двух переменных и от нее вновь можно вычислять частные производные и так далее.

Функция двух переменных имеет следующие вторые производные:

- вторая производная от f (x, y) по х дважды

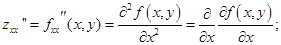
- вторая производная от f (x, y) по y дважды

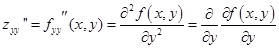
- вторая смешанная производная от f (x, y) по x и по y

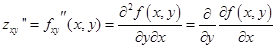
- вторая смешанная производная от f (x, y) по y и по х.

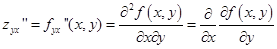
для функций, имеющих непрерывные частные производные второго порядка, смешанные производные второго порядка совпадают

Пример 2 ( продолжение примера 1). Вычислить вторые производные для функции

f (x, y) = x ³ y ² + sin x - 4 y.

Решение. Применяя правила дифференцирования, получим

z _xx¢¢ = (3 x ² y ² + cos x)_х’ = 6 xy ² - sin x,

z_yy ¢¢ = (2 x ³ y – 4)_y’ = 2 x ³,

z_xy ¢¢ = (3 x ² y ² + cos x)_y’ = 6 x ² y = z_yx ¢¢.

Теперь не представляет труда решение задачи о вычислении производных любого порядка.

Пример 3. Вычислить четвертую производную, причем одну по х и три по y для функции

f (x, y) = 2 x ⁴ ּ ln y - cos(x + y ³) + x ³

В соответствии и правилами дифференцирования сложных функций и функций многих переменных имеем:

Производные от функций большего числа производных вычисляются по тем же правилам.

Пример 4. Пусть дана функция четырех переменных f(x,y,z,t)

f(x, y, z, t) = xz ³ t ² + yz ² cos(y ³ - t).

Решение. Вычислим вторую смешанную производную по аргументам z и t

Глава 3. Дифференциалы функции двух переменных

Полным дифференциалом df (x, y) функции f (x, y) называется выражение

(3.1)

Напомним, что по определению для независимых переменных Δ x =d x, Δ y =d y.

Частным дифференциалом по переменной х называется следующее выражение

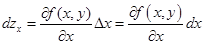(3,2)

Аналогично определяется частный дифференциал по переменной у

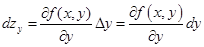(3.3)

Следовательно

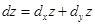(3.4)

Полное приращение функции двух переменных, вызванное приращением ее аргументов, отличается от полного дифференциала на бесконечно малую функцию более высокого порядка малости, чем приращения аргументов Δ х и Δ у, т.е.

D z = D f (x, y) = d f (x, y) + a(Δ x, Δ y) (3.5)

В этой связи на практике при небольших изменениях аргументов приращение функции заменяют на ее полный дифференциал. Если значение f (x ₀, y₀) известно, но неизвестно f (x ₁, y ₁) = f (x ₀+D x, y ₀+D y), то приближенное значение функции удобно вычислять при помощи полного дифференциала.

(3.6)

Пример 1. Найдем полный дифференциал функции .

Дата добавления: 2014-11-18