Основные свойства степенных рядов

1) Во всех точках, лежащих внутри интервала сходимости, сумма степенного ряда является непрерывной функцией переменной x:

2) Степенной ряд можно почленно интегрировать внутри интервала сходимости:

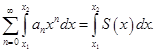
3) Внутри интервала сходимости степенной ряд можно почленно дифференцировать:

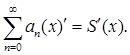
При почленном интегрировании и дифференцировании степенных рядов их интервалы сходимости не меняются.

Пример 4. Найти сумму ряда

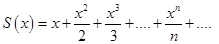(8.6)

Решение. Найдем сначала интервал сходимости этого ряда n

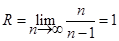
Следовательно, интервал сходимости ряда (-1, +1). Продифференцировав (5.6), имеем

S¢(x) = 1 + x + x² +... + xⁿ +....

Правая часть этого выражения - геометрический ряд с q = x, который сходится при ½x½<1. Поэтому, используя формулу суммы сходящейся геометрической прогрессии, получим

Отсюда сумму исходного ряда найдем интегрированием

Найдем C. Из (5.6) следует, что S(0) = 0. Следовательно,

0 = - ln (1-0) + C, C = 0.

Таким образом, S(x) = - ln (1-x) = .

Наряду со степенными рядами относительно переменной х часто рассматривают степенные ряды по переменной (x-a), т.е. ряды вида

C₀ + C₁(x-a) + C₂(x-a)² +... C_n (x-a)ⁿ +... (8.7)

Очевидно, что этот ряд подстановкой y = (x - a) превращается в ряд типа (5.3). Поэтому, если степенной ряд (5.3) имеет интервал сходимости - R < x < R, то соответствующий ряд вида (8.7) имеет интервал сходимости (a - R) < x < (a + R), центр которого расположен в точке x = a.

Ряд Тейлора. Пусть функция f(x) в точке х = а имеет производные любого порядка. Предположим, что имеется сходящийся степенной ряд

а₀ + а₁(x-a) + а₂(x-a)² +...+ а_n (x-a)ⁿ +... = (8.8)

сумма которого равна функции f(x), т.е.

(8.9)

Найдем коэффициенты такого ряда. Очевидно, что f(a) = а₀. Продифференцировав (8.8) в точке х=а, имеем а₁=f¢(a). Продифференцировав (8.8) в точке х=а дважды, получим а₂ = (f¢¢(a))/2. Продолжая дифференцирование равенства (8.8) можно убедится, что коэффициенты ряда (находятся по формуле

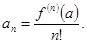
Степенной ряд вида

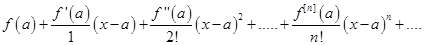
называется рядом Тейлора для функции f(x).

В частном случае при a= 0 ряд Тейлора имеет вид

f(x) = (8.10)

и его называют рядом Маклорена.

Пример 5. Разложить в ряд Тейлора функцию f(x) = e^x.

Решение. Поскольку e^x =(e^x)¢=(e^x)¢¢ =...(e^x)ⁿ, то при x=0 для f(x)= e^x имеем

f(0) = 1; f¢(0) = 1; f¢¢(0) = 1;...; f⁽ⁿ⁾(0) = 1;....

Следовательно, ряд Маклорена функции y = e^x имеет вид

e^x = 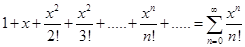(8.11)

Ряд (8.11) сходится на всей числовой оси к функции y=e^x.

Пример 6. Разложить в ряд маклорена функцию f(x) = sinx.

Решение. Для функции f(x) = sin x имеем:

Следовательно, ряд Маклорена для sin x:

или

Аналогично получается разложение для функции cos x:

или

cosx= .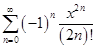

Подобным образом можно получить разложения в ряд Тейлора или Маклорена и многих других функций.

Раздел 8. Дифференциальные уравнения

Глава 1. Основные понятия теории дифференциальных уравнений

Пусть x - независимая переменная, y(x) - неизвестная функция этой переменной. y¢, y¢¢,..., y⁽ⁿ⁾ - производные неизвестной функции. Уравнение, связывающее независимую переменную х с функцией y(x) и ее производными до порядка n включительно, называется обыкновенным дифференциальным уравнением.

F (x, y, y¢, y¢¢,..., y⁽ⁿ⁾) = 0. (1.1)

Порядком дифференциального уравнения называется наивысший порядок производной, входящей в уравнение.

Дифференциальное уравнение n-го порядка может не содержать некоторые из величин x, y, y¢,..., y^(n-1) или даже все эти величины, но оно обязательно содержит n-ю производную y⁽ⁿ⁾.

Пример 1. y¢ + 2y = 0 - уравнение 1-го порядка, так как наивысший порядок производной равен единице.

Пример 2. y⁽⁴⁾ - y¢ = 0 - уравнение 4-го порядка: входят производные 1-го и 4-го порядков, наивысший порядок производной равен 4.

Решение дифференциального уравнения - это функция y = y₀(x), которая, будучи подставлена в уравнение, обращает его в тождество:

F (x, y₀(x), y₀¢,..., y₀⁽ⁿ⁾(x)) º 0.

Пример 3. Пусть дано уравнение y¢¢ + y = 0. Покажем, что функция y = sinx является решением этого уравнения.

Имеем y¢= (sin x)¢ = cosx, y¢¢= (cosx)¢= - sinx. Подставим в уравнение вместо y и y¢ функции sinx и - sinx:

- sin x + sin x º 0.

Покажем, что функция y = C₁ cosx + C₂ sinx, где C₁ и C₂ - произвольные постоянные, также является решением данного уравнения. Имеем

y¢ = - C₁ sinx + C₂ cosx; y¢¢ = - C₁ cosx - C₂ sinx.

Подставим в уравнение выражения y и y¢¢:

- C₁ cos x - C₂ sin x + (C₁ cos x + C₂ sin x) º 0.

График решения y = y(x) называется интегральной кривой. Задача нахождения решений дифференциального уравнения называется задачей интегрирования дифференциального уравнения.

Рассмотрим уравнение n-го порядка, разрешенное относительно старшей производной:

y⁽ⁿ⁾ = f (x, y, y¢,..., y^(n-1)). (1.2)

Такая запись уравнения называется видом разрешенным относительно старшей производной.

Предполагаем, что функция f определена, однозначна и непрерывна в некоторой области изменения своих аргументов. Задача нахождения решения y = y(x), удовлетворяющего заданным начальным условиям: при x = x₀

y = y₀, y¢= y₀¢,..., y₀^(n-1) = y_o^(n-1), (1.3)

где x₀, y₀, y₀¢,..., y₀^(n-1) суть заданные числа (начальные данные), называется задачей Коши.

Начальные условия можно записать и так:

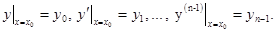
Дадим определения общего и частного решений уравнения n-го порядка y⁽ⁿ⁾ = f(x, y, y¢,..., y^(n-1)), правая часть которого есть функция определенная и непрерывная в некоторой области G изменения переменных x, y, y¢,...,y^(n-1). Функция

y = j(x,C₁,C₂,...,C_n), (1.4)

зависящая от аргумента x и n произвольных постоянных C₁, C₂,..., C_n, называется общим решением уравнения(1.2) в области G, если она удовлетворяет двум условиям:

1) функция (1.4) является решением уравнения (1.2) при любых значениях произвольных постоянных C₁, C₂,...,C_n;

2) каковы бы ни были начальные условия (1.3), существует единственный набор постоянных C₁⁰, C₂⁰,...,C_n⁰, такой, что функция y= j(x,C₁⁰, C₂⁰,..., C_n⁰) является решением уравнения (1.2) и удовлетворяет начальным условиям (1.3).

Чтобы найти решение уравнения (1.2) с начальными данными x₀, y₀, y₀¢, y₀^(n-1) из области G, если известно общее решение (1.2) поступают следующим образом:

1) составляют систему уравнений

(1.5)

2) решая систему (1.5), находят C₁⁰, C₂⁰,..., C_n⁰;

3) подставляют найденные значения произвольных постоянных в общее решение(1.4) и получают искомое решение

y= j(x,C₁⁰, C₂⁰,..., C_n⁰),

которое является искомым единственным решением задачи.

Если общее решение уравнения (1.2) задано в неявном виде

Ф(x, y,C₁, C₂,..., C_n) = 0 (1.6)

то оно называется общим интегралом дифференциального уравнения.

Всякое решение, получаемое из общего решения (1.4) при конкретных значениях постоянных C₁ = C₁⁰, C₂ = C₂⁰,..., C_n = C_n⁰, называется частным решением уравнения(1.2).

Пример 4. Дано уравнение y¢¢ + y = 0. Найти его частное решение, удовлетворяющее начальным условиям: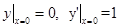

Решение. Выше было показано, что функция y= C₁ cos(x) + C₂ sin(x), где C₁, C₂ - произвольные постоянные, является решением данного уравнения. Это общее решение. Для нахождения частного решения используем начальные условия: x₀ = 0, y₀ = 0. Заметим, что при этих условиях y¢ = 1.

Составим систему типа (4.65)

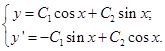
Для заданных начальных условий имеем

Найденные значения C₁⁰, C₂⁰ подставим в общее решение:

y = C₁⁰ cosx + C₂⁰ sinx Þ y = sinx.

Итак, искомое частное решение уравнения y = sin(x).

Глава 2. Дифференциальные уравнения первого порядка

Дифференциальное уравнение первого порядка - это уравнение, в которое входят независимая переменная, неизвестная функция и первая производная этой функции. Общий вид дифференциального уравнения первого порядка

F (x, y, y¢) = 0. (2.1)

Здесь F - заданная функция трех аргументов. Она может не зависеть от x или y (или от обеих переменных), но должна содержать y¢.

Если уравнение (2.1) разрешить относительно y¢, то получим разрешенный вид

y¢ = f(x,y), (2.2)

где f - заданная функция от x и y. В дальнейшем мы будем рассматривать только уравнения в разрешенном виде.

Решение дифференциального уравнения (2.2) - это функция y = y₀(x), которая, будучи подставлена в это уравнение, обращает его в тождество:

y₀¢(x) º f(x,y₀).

Пример 1. Дано уравнение y¢ + y ctg x - 2cos x = 0.

Покажем, что функция y = sin x является его решением. Для этого подставим в данное уравнение вместо y и y¢ функции sinx и (sinx)¢ = cosx. Имеем:

cosx + sinx ctgx - 2cosx = cosx + cosx - 2cosx º 0.

Уравнение обратилось в тождество.

Функция

y = j (x,C) (2.3)

называется общим решением уравнения (2.2), если она является решением этого уравнения при всех значениях произвольной постоянной C.

Если общее решение задано в неявном виде j(x,y,C) = 0, то оно называется общим интегралом. Частное решение уравнения (2.2) - это решение, которое получается из общего (2.3) при конкретном значении C.

Для дифференциального уравнения (2.2) задача Коши формулируется так: среди всех решений уравнения найти решение y = y(x), удовлетворяющее условию

(2.4)

где x₀, y₀ - заданные числа.

Условие (2.4) называется начальным условием, а числа x₀, y₀ - начальными значениями.

Уравнения с разделяющимися переменными - это уравнение, правая часть которого f(x,y) есть произведение двух сомножителей f(x) и g(y), каждый из которых зависит только от одной переменной

y¢ =f(x)ּg(y). (2.5)

Уравнения с разделяющимися переменными интегрируются следующим образом: y¢ заменяется на 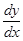, затем умножаются обе части (2.5) на .

Получим:

(2.6)

Дифференциалы переменных x и y, и соответствующие функции стоят отдельно, т.е переменные отделены.

Если обозначить G(y) = , F(x) = , то уравнение (2.6) можно переписать в виде

dG(y) = dF(x).

Так как из равенства дифференциалов двух функций следует, что сами функции отличаются на произвольное постоянное слагаемое, то

G(y) = F(x) + C

или

= f(x)dx + C. (2.7)

Выражение (2.7) представляет собой общий интеграл уравнения (2.5). Вычислив интегралы в (2.7), получим решение исходного уравнения

Пример 2. Решить уравнение xy¢+ y = 0.

Решение. Разрешим уравнение относительно y¢: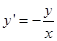

Здесь f(x) = -1/х, а g(y) = y.

Заменим в этом уравнении y¢ на dy/dx и умножим обе части уравнения на dx/y:

Получили уравнение с разделенными переменными. Интегрируя, находим ,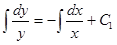

где C₁ - произвольная постоянная.

Отсюда следует: ln ½y½ = - ln½x½ + C₁.

В данном случае удобно вместо C₁ написать ln C₂ (C₂ > 0).

Тогда ln ½y½ = - ln ½x½ + ln C₂

или

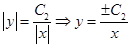
Так как ±C₂ принимает любые значения, то обозначая ±C₂ = C, окончательно получим

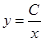
где C - произвольная постоянная.

Эта формула и дает общее решение заданного уравнения. Найдем теперь частное решение, удовлетворяющее начальному условию y½_x=4 = 1/2. Для этого в равенство y = C/х подставим вместо x и y значения 4 и 1/2. Получим 1/2 = C/4. Отсюда следует, что C = 2. Таким образом, искомое частное решение имеет вид y=2/х.

Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно искомой функции y(x) и ее производной y¢(x). В общем случае оно имеет вид

y¢ + p(x)y = f(x). (2.8)

Если f(x) º 0, то уравнение называется линейным уравнением без свободного члена (правой части) или линейным однородным уравнением. Итак,

y¢ + p(x)y = 0

линейное однородное уравнение (оно же уравнение с разделяющимися переменными).

Если f(x) ¹0, то уравнение (2.8) называется линейным неоднородным уравнением.

Например, уравнение y¢ - y cos²x = х² является линейным неоднородным уравнением. Однородное по отношению к нему будет уравнение y¢ - y cos²x = 0. Уравнение (2.8) можно интегрировать разными методами. Мы рассмотрим метод Бернулли. Он состоит в следующем. В уравнении (2.8) делаем замену:

y = u(х) ּ v(х), (2.9)

Дифференцируя по правилу «производная произведения двух функций», имеем

y¢ = u¢(х) ּv(х) + u(х) ּv¢(х) (2.10)

Подставим в уравнение (2.8) вместо y и y ¢ их выражения из (2.9) и (2.10), получим

u¢(х)v(х) + u(х)v¢(х) + p(х)u(х)v(х) = f(х)

или

u¢v + u[v¢ + p(x)v] = f(х). (2.11)

Так как одну из функций в (2.9) можно выбрать произвольно, то функцию v выберем таким образом, чтобы коэффициент при u обратился в нуль, т.е.

v¢ + p(x)v = 0. (2.12)

Уравнение (2.12) относительно функции v(x) является уравнением с разделяющимися переменными. Поэтому из (2.12) имеем:

Интегрируя, находим

Так как функция v - это любая функция, удовлетворяющая (2.8), то полагаем C=0.

Итак,

ln(v) = - pdx Þ .

Представляя найденную функцию v(x) в уравнение (2.8), получим

Отсюда следует

Интегрируя, получим

(2.13)

где C - произвольная постоянная. Для того, чтобы найти y(x), умножим найденную u(x) на v(x):

(2.14)

Формула (2.14) дает общее решение дифференциального уравнения (2.8).

Задача. Найти общее решение уравнения

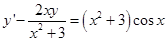
Решение. Это линейное неоднородное уравнение, где

Выполнив замену y = uּv, получаем y¢ = u¢v + uv¢.

Заданное дифференциальное уравнение перепишем в виде

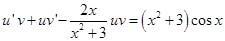
или

Приравняем выражение в скобках нулю:

Получили уравнение для функции v(x) - уравнение с разделяющимися переменными. Интегрируем его:

Подставляя функцию v(x) в уравнение, найдем уравнение для функции u(x):

u¢(x² + 3) = (x² + 3)cosx.

Отсюда следует

u¢ = cos(x) или u = cos(x) dx + C Þ u = sin(x) + C.

Теперь находим общее решение заданного уравнения y(x):

y = uv Þ y = (sin(x) + C)(x² + 3).

Глава 3. Линейные дифференциальные уравнения второго порядка

Дифференциальное уравнение второго порядка - это уравнение, в которое входят независимая переменная, неизвестная функция, первая и вторая производные этой функции. Общий вид дифференциального уравнения первого порядка

(3.1)

Здесь F - заданная функция четырех аргументов. Она может не зависеть от x, y и y’(или от обеих переменных), но должна содержать y’’.

Если уравнение (3.1) разрешить относительно y’’, то получим разрешенный вид

y’’ = f(x,y,y’), (3.2)

где f - заданная функция от x,y и y’. В дальнейшем мы будем рассматривать только уравнения в разрешенном виде.

Решение дифференциального уравнения (2.2) - это функция y = y₀(x), которая, будучи подставлена в это уравнение, обращает его в тождество:

y₀’’(x) º f(x,y₀, y₀’). (3.3)

Определение. Общим решением уравнения второго порядка называется такая функция

, (3.4)

которая при любых значениях произвольных постоянных C₁ и C₂ является решением этого уравнения.

Если заданы начальные условия (это называется задача Коши) 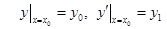, то подставляя начальные условия в общее решение получим частное решение. Конкретные значения постоянных C₁ и C₂ находятся из системы

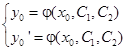
Определение. Линейным неоднородным уравнением второго порядка называется уравнение

, (3.5)

где p(x), q(x) – коэффициенты уравнения, а f(x) – правая часть уравнения.

Если f(x) =0, то уравнение называется однородным

(3.6)

Если коэффициенты p(x) и q(x) постоянны, т.е. не зависят от х, то это уравнение называют уравнением с постоянными коэффициентами и записывают его так:

. (3.7)

Решением такого уравнения может быть только функция не меняющая свой вид при дифференцировании, т. е.

. (3.8)

Подставляя функцию и производные в уравнение (3.7), получим

.

В этом выражении при любых значениях k и x, поэтому на него можно сократить.

Определение. Уравнение

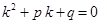(3.9)

которое получается из линейного однородного уравнения, называется характеристическим уравнением.

Известно, что квадратное уравнение 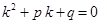имеет решение, зависящее от дискриминанта :

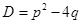1. Если , то корни k₁ и k₂ - действительные различные числа.

. Следовательно решениями будут функции и .

В качестве общего рещения берется их линейная комбинация с произвольными постоянными C₁ и C₂

. (3.10)

2. Если 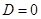, то k₁ = k₂, . Тогда в качестве общего решения берется следующее выражение

(3.11)

3.Если 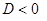, то решениями уравнения будут два комплексных числа

, где введены обозначения , , а .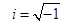

В этом случае можно использовать формулу (3.10), подставляя 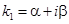, а 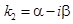, но удобнее сделать преобразование и записать общее решение в виде

(3.12)

Пример 1. Найти общее решение уравнения .

Решение. Ищем решение уравнения в виде 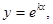тогда 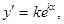и, подставляя в исходное уравнение получим 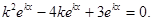Так как то на него можно сократить и мы получим

Находим его корни

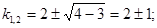
Корни характеристического уравнения вещественные, различные, значит, общее решение дифференциального уравнения имеет вид

или

Пример 2. Найти общее решение уравнения

Решение. Составляем характеристическое уравнение (см. пример 1)

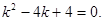
Решаем его

Корни характеристического уравнения вещественные равные. Общее решение дифференциального уравнения имеет вид

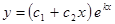
или

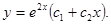
Пример 3. Найти общее решение уравнения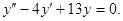

Решение. Составляем характеристическое уравнение (см. пример 1)

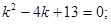
Корни характеристического уравнения комплексные сопряженные, значит, общее решение дифференциального уравнения имеет вид

Пример 4. Найти частные решения однородных линейных дифференциальных уравнений второго порядка, удовлетворяющие указанным начальным условиям:

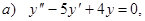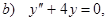где

где

Решение. а) находим общее решение (см. пример 1)

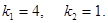
Общее решение

Дальше решаем задачу Коши. Постоянные 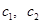найдем с помощью начальных условий, вычислив предварительно производную от общего решения

Подставляя начальные условия в общее решение и его производную, получим

.

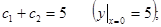
Из этой системы находим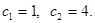

Подставив значения постоянных в общее решение, получим искомое частное решение

в) решаем второе уравнение. Его характеристическое уравнение имеет вид

Находим корни: Общее решение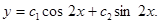

Вычисляем:

Подставляя начальные условия, получаем

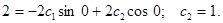
Частное решение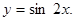

Общим решением неодногодного уравнения будет сумма общего решения однородного уравнения и частного решения неоднородного уравнения.

Укажем способ, позволяющий найти частное решение неоднородного уравнения по виду правой части. Заметим, что это возможно лишь в случаях, когда правая часть уравнения является функцией определенного вида.

1. Пусть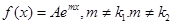

Тогда частное решение ищут в виде 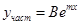. Коэффициент В находят непосредственной подстановкой частного решения в уравнение. Общее решение имеет вид

2. , .

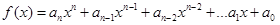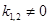Тогда частное решение ищут в виде

.

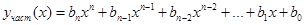3. Если , то

.

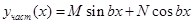Если справа стоит сумма или произведение двух функциий, то в качестве частного решения берется соответственно сумма или произведение соответствующих функций.

Пример 5. Найти общее решение уравнения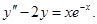

Решение. Находим сначала общее решение соответствующего однородного уравнения

Характеристическое уравнение Его корни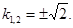

Общее решение однородного уравнения

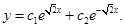
Теперь следует найти частное решение 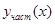неоднородного уравнения. Правая часть 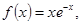значит 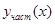ищем в форме , т.к. не является корнем характеристического уравнения.

Требуется найти неизвестные коэффициенты А и В. Для определения А и В дифференцируем дважды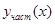

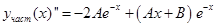
и подставляем это в данное неоднородное уравнение:

Так как то сократив 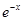, получим тождественное равенство двух полиномов

Значения А и В найдем, приравнивая коэффициенты при одинаковых степенях 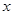в левой и правой частях

при Х:

при Х^°: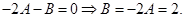

Подставляем найденные А и В в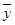

Общее решение неоднородного уравнения

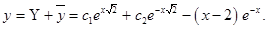
Пример 6. Найти общее решение уравнения

Решение. Соответствующее однородное уравнение

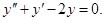
Составляем характеристическое уравнение и решаем его

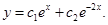
Правая часть данного неоднородного уравнения

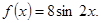
Следовательно, частное решение 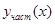разыскиваем в виде

,

т.к. 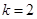не является решением характеристического уравнения.

Дифференцируем и подставляем это решение в неоднородное уравнение

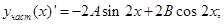
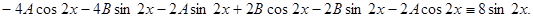
Приравниваем коэффициенты при одинаковых тригонометрических функциях в левой и правой частях тождества

при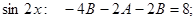

при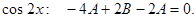

Из этой системы находим А и В

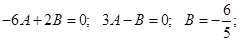
Общее решение

Пример 7. Найти частное решение уравнения 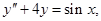удовлетворяющее начальным условиям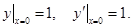

Решение. Чтобы найти частное решение, удовлетворяющее заданным начальным условиям, необходимо получить сначала общее решение данного неоднородного уравнения. Находим его (см. пример 6)

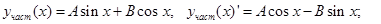
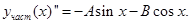
Подставляем 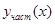в уравнение

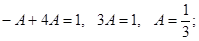
Искомое частное решение будем находить из общего. Общее решение неоднородного уравнения

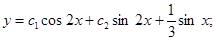
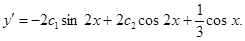
Подставляем начальные условия. При 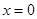имеем

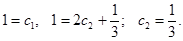
Найденные постоянные подставляем в общее решение неоднородного уравнения

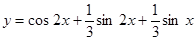
искомое частное решение.

Заключение

Изучение математики в высшем учебном заведении преследует разные цели. Это и тренировка логического мышления, и возможность решать математическими методами всевозможные прикладные задачи и изучение универсального символьного языка, который используется в естественно-научных и технических дисциплинах.

Дальнейшее изучение математики предполагает изучение следующих разделов: Теория вероятностей и Математическая статистика.

Эти дисциплины носят прикладной характер, но их изучение невозможно без знания основных сведений, изложенных в нашем курсе математики.

Учебное издание

МАТЕМАТИКА

Часть 2 Учебное пособие Оригинал-макет подготовлен автором и издан в авторской редакции  

Подписано в печать 27.03.2013 г. Формат 60х84 1/16.

Усл. печ. л. 4,3. Тираж 100 экз. заказ 55/13.

Электронный адрес: http://alt-rinpo.sutd/ru

Отпечатано в типографии ФГБОУВПО «СПГУТД»

191028, Санкт-Петербург, ул. Моховая, 26

Дата добавления: 2014-11-18