Транспонирование матриц

Определение 1.9. Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной относительно данной.

Матрицу, транспонированную относительно матрицы A, обозначают A^Т. Таким образом, если

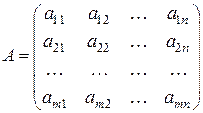, то (1.5)

Отмети, что если A – матрица размера m ´ n, то матрица A^Т имеет размер n ´ m. Операция нахождения матрицы, транспонированной к данной, называется транспонированием матрицы.

2. ОПРЕДЕЛИТЕЛИ

Квадратной матрице A порядка n можно сопоставить число 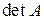(или , или ), называемое ее определителем.

Для матрицы первого порядка, т.е. 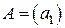, определителем будет .

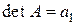Определение 2.1. Определителем 2-го порядка матрицы 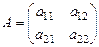называется число, записанное в виде квадратной таблицы и вычисляемое, согласно указанному правилу

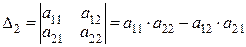. (2.1)

Пример 2.1. Найти определители 2-го порядка: .

,

Определение 2.2. Определителем 3-го порядка матрицы называется число, записанное в виде квадратной таблицы и вычисляемое, согласно указанному правилу

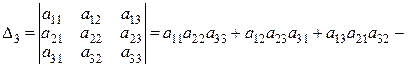
(2.2)

Заметим, что каждое слагаемое алгебраической суммы в правой части представляет собой произведение элементов определителя, взятых по одному и только по одному из каждой строки и каждого столбца. Этому произведению приписывается соответствующий знак. Чтобы помнить, какие произведения следует брать со знаком плюс, какие – со знаком минус, можно пользоваться правилом, схематически изображенным на рисунке.

«+» «-»

Пример 2.2. Найти определитель 3-го порядка.

.

,

Правило, по которому находиться определитель 3-го порядка (определение 2.2.), называется правилом треугольника (правило Саррюса). Но для более удобного вычисления определителя 3-го порядка можно применить правило приписывания к определителю справа первых двух ее столбцов.

«-» «-» «-» «+» «+» «+»

Определитель матрицы A также называют детерминантом. Правило вычисления детерминанта для матрицы n -го порядка является довольно сложным для восприятия и применения. Однако известны методы, позволяющие реализовать вычисление определителей высоких порядков на основе определителей низших порядков. Один из методов основан на свойстве разложения определителя по элементам некоторого ряда, который рассмотрим несколько позже. При этом заметим, что определители невысоких порядков (1-го, 2-го и 3-го) желательно вычислять согласно определению.

Определение 2.3. Минором M_ij некоторого элемента 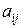называется определитель, полученный из исходного вычеркиванием i -ой строки и j -го столбца, на пересечении которых находится выбранный элемент.

Например, для определителя 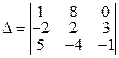минор элемента 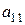будет 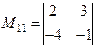, а минор элемента будет 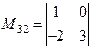. Для определителя 2-го порядка 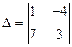минор элемента 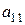будет .

Определение 2.4. Алгебраическим дополнением A_ij некоторого элемента 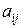называется его минор, взятый со знаком , т.е.

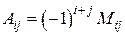. (2.3)

Например, для определителя 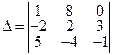алгебраическое дополнение элемента 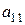будет 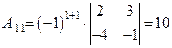, а алгебраическое дополнение элемента будет .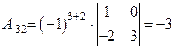

Каждый определитель состоит из строк и столбцов. В дальнейшем строки и столбцы будем называть рядами определителя.

Определение 2.5. Определителем матрицы n-го порядка

называется число, равное сумме произведений элементов его произвольного ряда на их алгебраические дополнения, т.е. справедлива одна из формул:

, (2.4)

называемая разложением определителя по i-ой строке, или

, (2.5)

называемая разложением определителя по j-ому столбцу.

Пример 2.3. Найти определитель 3-го порядка, используя разложение по второй строке.

,

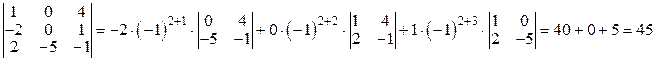3. ОБРАТНАЯ МАТРИЦА

3.1. Теорема существования обратной матрицы

Определение 3.1. Квадратная матрица A называется невырожденной, если ее определитель 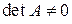. В противном случае матрица A называется вырожденной или особенной.

Определение 3.2. Матрицей, присоединенной к матрице A, называется матрица вида

,

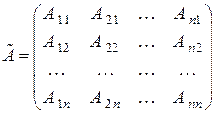где 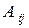- алгебраическое дополнение элемента 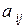данной матрицы A (оно определяется так же, как и алгебраическое дополнение элемента определителя).

Определение 3.3. Матрица 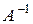называется обратной матрице A, если выполняется условие

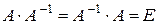, (3.1)

где E – единичная матрица того же порядка, как и матрица A.

Матрица 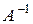имеет тот же порядок, что и матрица A.

Пример 3.1. Показать,что матрица A является обратной для матрицы B, если

.

Решение. Найдем произведение матриц A и B.

.

Аналогично . Следовательно, матрица A является обратной для B.

,

Теорема 3.1. Для невырожденной матрицы A существует единственная обратная матрица 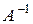, определяемая формулой

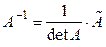, (3.2)

где - матрица, присоединенная к матрице A.

Теорему 3.1 примем без доказательства.

Пример 3.2. Найти 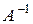, если .

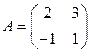Решение. 1) Находим определитель матрицы A.

.

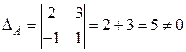Матрица A – невырожденная, значит, существует ей обратная.

2) Находим алгебраические дополнения элементов матрицы A.

.

Составляем матрицу, присоединенную к матрице A.

.

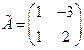3) Находим .

.

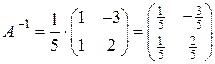Сделаем проверку:

,

Дата добавления: 2014-11-18