
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Общие сведения о гидравлических потерях
|
|
|
|
Гидравлические сопротивления
Движение вязкой жидкости сопровождается потерями энергии.
Потери удельной энергии (напора), или гидравлические потери, зависят от формы, размеров русла, скорости течения и вязкости жидкости.
В большинстве случаев гидравлические потери 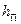 пропорциональны скорости течения жидкости во второй степени или динамическому напору
пропорциональны скорости течения жидкости во второй степени или динамическому напору  и определяются из выражения
и определяются из выражения
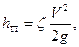 (4.1)
(4.1)
где 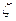 - коэффициент потерь; V- средняя скорость в сечении.
- коэффициент потерь; V- средняя скорость в сечении.
Потери в единицах давления
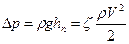 . (4.2)
. (4.2)
Гидравлические потери энергии обычно разделяют на местные потери и потери на трение по длине
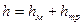 . (4.3)
. (4.3)
Местные потери энергии обусловлены так называемыми местными гидравлическими сопротивлениями, т.е. местными изменениями формы и размеров русла, вызывающими деформацию потока. При протекании жидкости через местные сопротивления изменяется ее скорость и возникают вихри.
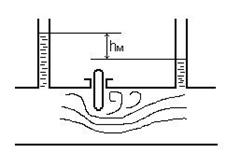
Примером местных сопротивлений может служить задвижка (рис.4.1).
|
| Рисунок 4.1 – Местное гидравлическое сопротивление: а) задвижка |
Местные потери напора определяются по формуле Вейсбаха
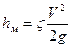 , (4.4)
, (4.4)
где V-средняя скорость в трубе; 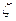 -коэффициент местного сопротивления.
-коэффициент местного сопротивления.
Потери на трение по длине 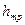 -это потери энергии, которые возникают в прямых трубах постоянного сечения и возрастают прямо пропорционально длине трубы (рис.4.2).
-это потери энергии, которые возникают в прямых трубах постоянного сечения и возрастают прямо пропорционально длине трубы (рис.4.2).
Рассматриваемые потери обусловлены внутренним трением жидкости в трубах. Потери напора при трении определяются по формуле Дарси-Вейсбаха
 , (4.5)
, (4.5)
где λ – коэффициент гидравлического трения по длине или коэффициент Дарси; l – длина трубопровода; d –его диаметр; V – средняя скорость течения жидкости.

|
| Рисунок 4.2 – Потери напора по длине трубы |
Для ламинарного режима движения жидкости в круглой трубе коэффициент 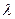 определяется по теоретической формуле
определяется по теоретической формуле
|
|
|
 , (4.6)
, (4.6)
где 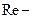 число Рейнольдса.
число Рейнольдса.
При турбулентном режиме коэффициент 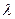 зависит от числа Рейнольдса Re и относительной шероховатости
зависит от числа Рейнольдса Re и относительной шероховатости 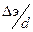 (
(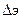 -эквивалентная шероховатость) и определяется по эмпирическим формулам.
-эквивалентная шероховатость) и определяется по эмпирическим формулам.
В области гидравлически гладких труб 4000<Re< 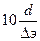 , т.е. прималых скоростях и числах Рейнольдса, коэффициент Дарси зависит только от числа Рейнольдса, и его определяют по формуле Блазиуса
, т.е. прималых скоростях и числах Рейнольдса, коэффициент Дарси зависит только от числа Рейнольдса, и его определяют по формуле Блазиуса
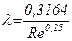 . (4.7)
. (4.7)
В переходной области (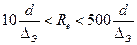 ) на коэффициент Дарси влияют шереховатость и число Рейнольдса. В этой области для вычислений используют формулу Альтшуля
) на коэффициент Дарси влияют шереховатость и число Рейнольдса. В этой области для вычислений используют формулу Альтшуля
 . (4.8)
. (4.8)
В квадратичной области сопротивления (области гидравлически шероховатых труб) коэффициент 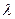 может быть найден по формуле Шифринсона
может быть найден по формуле Шифринсона
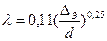 . (4.9)
. (4.9)
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 487; Нарушение авторских прав?; Мы поможем в написании вашей работы!