Линейного программирования

СВЕДЕНИЕ МАТРИЧНОЙ ИГРЫ К ЗАДАЧЕ

Оптимальные стратегии для игрока 2 можно найти из системы

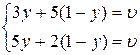Þ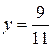

и, следовательно, 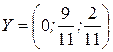). (Из рисунка видно, что стратегия B₁ не войдёт в оптималь­ную стратегию.

Пример 2. Найти решение игры, заданной матрицей

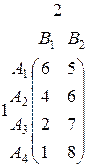
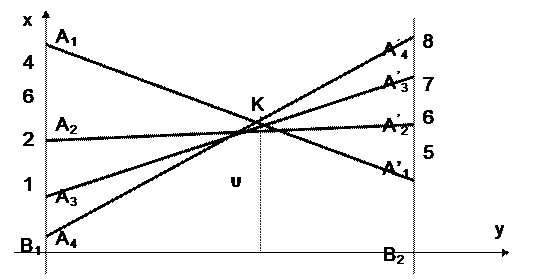
Решение. Матрица имеет размерность 2х4. Строим прямые, соответствующие стратеги­ям игрока 1. Ломанная A₁ К А'₄ соответствует верхней границе выигрыша игрока 1, а отрезок N К - цене игры. Решение игры таково

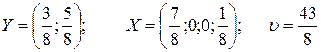
Предположим, что цена игры положительна (u > 0). Если это не так, то согласно свойству 6 всегда можно подобрать такое число с, прибавление которого ко всем элементам матрицы выигрышей даёт матрицу с положительными элементами, и следовательно, с положительным значением цены игры. При этом оптимальные смешанные стратегии обоих игроков не изменя­ются.

Итак, пусть дана матричная игра с матрицей А порядка т х п. Согласно свойству 7 опти­мальные смешанные стратегии х = (x₁,..., х_m), у = (y₁,..., у_n) соответственно игроков 1 и 2 и це­на игры и должны удовлетворять соотношениям.

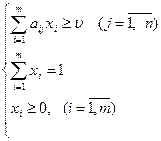(1)

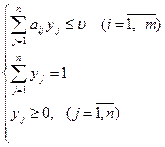(2)

Разделим все уравнения и неравенства в (1) и (2) на u (это можно сделать, т.к. по предположе­нию u > 0) и введём обозначения:

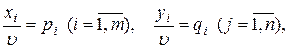
Тогда (1) и (2) перепишется в виде:

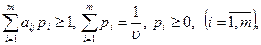
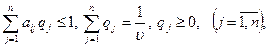
Поскольку первый игрок стремится найти такие значения х_i и, следовательно, p_i, чтобы цена игры u была максимальной, то решение первой задачи сводится к нахождению таких неотри­цательных значений р_i (i = 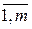), при которых

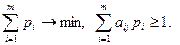
Поскольку второй игрок стремится найти такие значения y_j и, следовательно, q_j, чтобы цена иг­ры u была наименьшей, то решение второй задачи сводится к нахождению таких неотрица­тельных значений q_j (j = 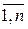), при которых

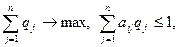(4)

Формулы (3) и (4) выражают двойственные друг другу задачи линейного программирования (ЛП).

Решив эти задачи, получим значения р_i (i = 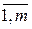), q_j (j = 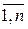) и u. Тогда смешанные стратегии, т.е. х_i и у_j получаются по формулам:

х, = up_i (i = ),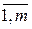

y = uq_j (j = 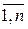) (5)

Пример. Найти решение игры, определяемой матрицей.

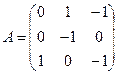
Решение. При решении этой игры к каждому элементуматрицы А прибавим 1 и получим следующую матрицу

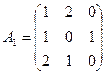
Составим теперь пару взаимно-двойственных задач:

p1 + p2 + p3 ® min	q1 + q2 + q3 ® max
p1 + p2 + 2p3 ³1, 2p1 + p3 ³1, p3 ³1, p1, p2, p3 ³0	q1 + 2q2 + £1, q1 + q3 £1, 2q1 + q2 £1, q1, q2, q3 ³0

Решим вторую из них

Б.п.	q1	q2	q3	q4	q5	q6	Решение	S	отношение
	-1	-1	-1					-3
q4			0						-
q5									1/1
q6									-

Б.п.	q1	q2	q3	q4	q5	q6	Решение	S	отношение
		-1
q4									1/2
q3									-
q6									1/1=1

Б.п.	q1	q2	q3	q4	q5	q6	Решение	S	отношение
	1/2			1/2			3/2	7/2
q2	1/2			1/2			1/2	5/2
q3
q6	3/2			-1/2			1/2	5/2

Из оптимальной симплекс-таблицы следует, что 7/2

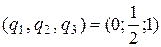
а из соотношений двойственности следует, что

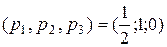
Следовательно, цена игры с платёжной матрицей A₁ равна

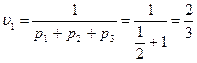
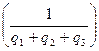
а игры с платёжной матрицей А:

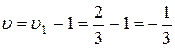
При этом оптимальные стратегии игроков имеют вид:

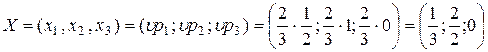
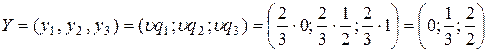
Теория графов имеет широкий спектр приложений, т.к. ее язык, с одной стороны, нагляден и понятен, а с другой – удобен в формальном исследовании. На языке теории графов формулируются и решаются многие задачи управления, в т.ч. задачи сетевого планирования, анализа и проектирования организационных структур управления, анализа процессов функционирования, многие задачи принятия решений в условиях неопределенности и рисковых ситуаций и др.

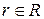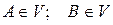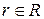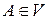Графом G называется совокупность двух непустых множеств: вершин V и ребер R, между элементами которых определено отношение инцидентности; каждое ребро инцидентно равно двум вершинам , которые оно соединяет. При этом вершина А (В) и ребро r называются инцидентными друг другу, а вершины А и В, являющиеся для ребра r конечными точками, называются смежными. Часто вместо и пишут .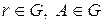

При изображении графов на рисунках или схемах отрезки мо

гут быть прямо- или криволинейными; длина отрезков и расположение точек - произвольные. Все три фигуры на рис.1 изображают один и тот же граф.

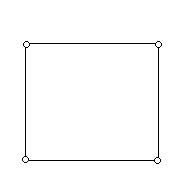
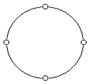
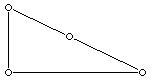
Рис. 1

Ребро, соединяющее две вершины, может иметь направление от одной вершины к другой; в этом случае оно называется направленным или ориентированным.

Граф, содержащий направленные ребра, называется ориентированным (орграфом), а ненаправленные – неориентированным (неорграфом). Ребра, инцидентные одной и той же паре вершин, называются параллельными, или кратными.

Граф, содержащий кратные ребра, называется мультиграфом. Ребро, концевые вершины которого совпадают, называется петлей.

Граф называется конечным, если множество его элементов (вершин и ребер) конечно, и пустым, если это множество пусто. Граф без петель и кратных ребер именуется полным, если каждая пара вершин соединена ребром.

Дополнением графа G называется граф 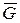, имеющий те же вершины, что и граф G, и содержащий только те ребра, которые нужно добавить к графу G, чтобы получить полный граф.

Локальной степенью вершины 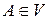н -графа G называется количество ребер 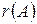, инцидентных вершине А. В н -графе сумма степеней всех вершин равна удвоенному числу ребер м графа. Петля добавляет число 2 в степень вершины

.

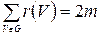Для вершин орграфа определяется две локальные степени:

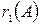- число ребер, исходящих из вершины А;

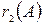- число ребер, входящих в вершину А.

Петля добавляет число 1 в каждую из этих степеней.

В орграфе суммы степене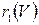й и 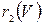равны количеству т ребер графа, т.е. равны между собой.

.

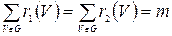Два графа равны между собой, если множество вершин и ребер, определяющие эти графы, равны соответственно между собой.

Путь от 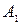до 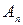называется простым, если он не проходит ни через одну вершину графа более одного раза.

Циклом называется путь, в котором совпадают его начальная и конечная вершины.

Простым циклом в графе называется цикл, не проходящий ни через одну из вершин графа более одного раза.

Длиной пути называется число ребер этого пути. Аналогично, длиной цикла называется число ребер в этом цикле.

Деревом называется всякий связный граф, не имеющий циклов (рис.2).

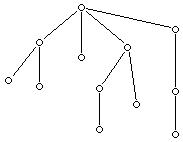
Рис. 2

Для каждой пары вершин дерева существует единственный соединяющий их путь. Вершина дерева со степенью, равной 1, называется висячей вершиной.

Лесом называется несвязный граф, представляющий объединение деревьев.

Способы задания графов.

Граф G считается полностью заданным, если нумерация его вершин и ребер зафиксирована.

Аналитический способ задания – в виде двух множеств вершин V и ребер R, когда каждое ребро r определено парой инцидентных ему вершин (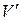 и 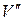). Граф G полностью определен двумя множествами: 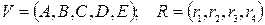или множеством ребер, представленных парой своих концевых вершин: .

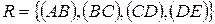Графический способ представлен на рис.3.

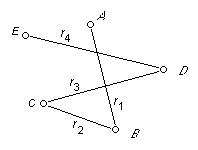G

Рис. 3

Порядок указания вершин в н -графе при описании ребер безразличен.

Рассмотрим другие способы, используемые в теории графов.

Матричный способ – описывает множество вершин и ребер графа и отношение инцидентности.

Матрица инцидентности 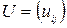размеренностью (m x n) – матрица, в которой по вертикали указываются вершины, по горизонтали – ребра, а на пересечении i -ой вершины и j -го ребра проставляется 1, если они инцидентны и 0 – в противном случае.

если G – H -граф.

Если же G – орграф, то

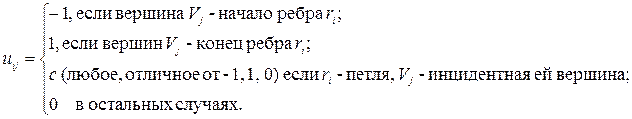Матрица смежности 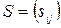- квадратная матрица размерностью (n x n), в которой по вертикали и горизонтали перечисляются все вершины 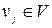. На пересечении k -ой и р -ой вершин проставляется:

в случае Н -графа – число ребер, соединяющих эти вершины;

в случае орграфа – число ребер с началом в k -ой вершине и концом в р -ой.

Свойства матриц 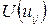и :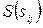

1. Если два графа равны, их матрицы совпадают.

2. Вид матриц зависит от нумерации вершин и ребер графа.

Графы, отличающиеся только нумерацией вершин, являются изоморфными.

Еще один способ – задание графа списком ребер. Это таблица, состоящая из двух столбцов. В левом перечисляются все ребра 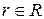, а в правом – инцидентные им вершины . Для Н -графа очередность вершин в строке любая; для орграфа – на 1-м месте стоит номер вершины – начало ребра.

Пример решения варианта заданий.

Задача 1. Задать матрицами инцидентности, смежности, списком ребер графы 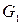и 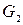(рис. 4).

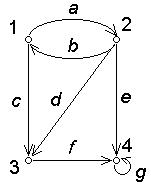
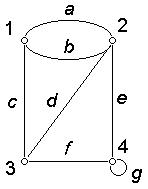
Рис. 4.

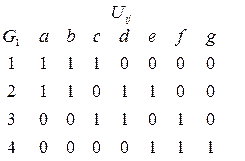
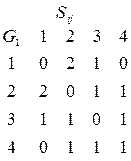
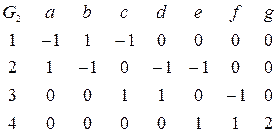
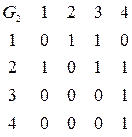
Список ребер

Ребра	Вершины
a
b
c
d
e
F
g

Список ребер Н -графа 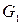аналогичен списку ребер орграфа 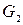, только последовательность указания вершин здесь безразлична.

Задача №2. Сетевая модель некоторого производственного процесса представлена на рис. 5. Задать сетевой граф различными способами.

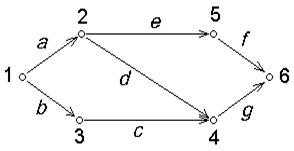
Рис. 5.

Сетевая модель представляет собой орграф, в котором ребра – операции производственного процесса, а вершины – события, характеризующие завершение одних операций и начало других. Направленность стрелок отражает последовательность наступления этих событий. Орграф может быть полностью задан следующими способами:

1. Графически (см. рис. 5)

2. двумя множествами:

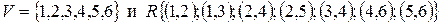
3. матрицей инцидентности:

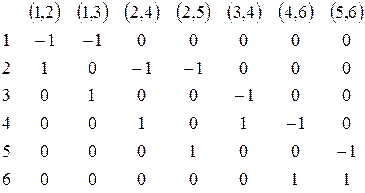
4. матрицей смежности:

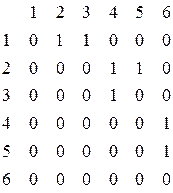
списком ребер:

Ребра	Вершины
a
b
c
d
e
f
g

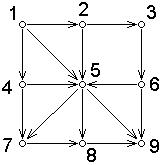Задача 3. Передвигаться по схеме можно только в указанном направлении, в каждом пункте быть не более 1 раза. Сколькими способами можно попасть из пункта 1 в пункт 9? У какого пути наименьшая (наибольшая) длина?

Решение.

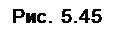Решить поставленную задачу помогают деревья. Строим орграф (n =9) – схему местности (рис. 6).

Начиная с вершины 1 последовательно перестраиваем граф в дерево (рис. 7). Каждая вершина столько раз получит самостоятельное значение, сколько в нее входило путей в первоначальном графе.

Рис. 7

Наикротчайший путь заканчивается в меньшем ярусе висячей вершины дерева, самый длинный – в наибольшем ярусе.

Число путей равно числу висячих вершин дерева 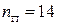. Длина кратчайшего пути 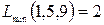. Длина самого продолжительного пути .

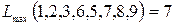Этот пример показывает, что понятие «длина пути» в теории графов не обязательно совпадает с понятием «длина пути» в геометрии или в географии.

Рисунок дерева полезен не только тем, что позволяет подсчитать число всех возможных путей, отыскать среди них кратчайший и наиболее протяженный. Он позволяет еще одновременно «увидеть» все пути и сравнить их.

Дата добавления: 2014-11-08