Основные формулы. 1) Формула Бернулли имеет вид

1) Формула Бернулли имеет вид

где Р_т,n - вероятность наступления события А т раз (с частотой т) при n независимых повторных испытаниях;

р = Р(А) - вероятность появления события А в одном ис­пытании;

q = Р( 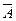) = 1 - р - вероятность не наступления события А в каждом испытании.

Число т₀ называется наивероятнейшим числом наступле­ний события А в п испытаниях, если значения Р_т,n при т = т₀ не меньше остальных значений Р_т,п. Если р≠0 и р≠ 1, то наивероятнейшее число определяется по формуле: np-q ≤т₀≤пр + p.

Разность граничных условий в двойном неравенстве равна единице.

2) Локальная асимптотическая формула Муавра-Лапласа

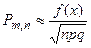, где и .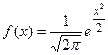

Условия применения: п - велико, а р и q - не очень малы, так что npq≥ 20; функция f(x) табулирована и является четной, т.е. φ(-x)=φ(x).

3) Асимптотическая формула Пуассона имеет вид

, .

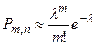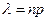Условия применения: п - велико, р - мало, так что пр ≤ 10; функция Пуассона есть функция двух переменных, табулирована.

4) Особое внимание следует обратить на простейший поток событий.

Потоком событий называют последовательность событий, которые наступают в случайные моменты времени. Примеры по­токов: поступление вызовов на АТС, поступление вызовов на пункт неотложной медицинской помощи, прибытие кораблей в порт, по­следовательность отказов элементов некоторого устройства.

Простейшим называют поток, обладающий свойствами ста­ционарности, отсутствием последействия и ординарности.

Свойство стационарности характеризуется тем, что веро­ятность появления k событий за время длительностью t не зави­сит от начала отсчета промежутка времени, а зависит лишь от его длительности. Так вероятности появления пяти событий на про­межутках времени (1; 4), (6; 9), (8; 11) одинаковой длительности t = 3 единицы времени равны между собой.

Свойство отсутствия последействия характеризуется тем, что вероятность появления k событий на любом промежутке вре­мени не зависит от того, сколько событий появилось до начала рассматриваемого промежутка.

Свойство ординарности характеризуется тем, что вероят­ность появления двух и более событий пренебрежимо мала, срав­нительно с вероятностью появления одного события.

Интенсивностью потока λ называют среднее число собы­тий, которые появляются в единицу времени. Доказано, что если известна постоянная интенсивность потока λ, то вероятность появления k событий простейшего потока за время длительности t о пределяется формулой:

.

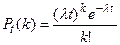Асимптотическая интегральная формула Муавра-Лапласа

,

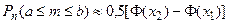где 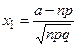, , 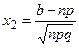, Ф(х) – функция Лапласа, нечетная Ф(-х) = -Ф(х), табулирована.

Запишем следствия из асимптотической интегральной фор­мулы Муавра-Лапласа:

а) Вероятность отклонения числа т наступлений события А от среднего значения п р определяется по формуле

.

б) Вероятность отклонения частности 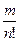от среднего значения р:

.

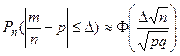Пример 17. Частица находится на прямой в начале координат. Под действием случайных толчков частица каждую секунду перемещается вправо (с вероятностью ) или влево (с вероятностью 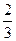) на единицу масштаба. Найти вероятность того, что через 4 секунды частица вернется в начало координат.

Решение. Через 4 секунды частица вернется в начало коор­динат в том случае, если она переместится ровно два раза вправо (и, значит, два раза влево). По формуле Бернулли найдем вероят­ность того, что из четырех независимых перемещений частицы ровно два перемещения будут вправо:

.

.

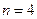
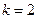
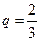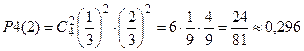Пример 18. К электросети подключено 36 приборов, каж­дый мощностью 5 киловатт и потребляет в данный момент энер­гию с вероятностью 0,2. Найти вероятность того, что потребляе­мая в данный момент мощность:

а) составит ровно 50 киловатт;

б) превзойдет 50 киловатт.

Решение. В случае а) надо найти вероятность того, что из 36 приборов работают ровно 10. Применим локальную теорему Лапласа: .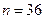

.

.

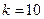
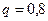Значение функции локальной функции Лапласа φ(х) взято из таблицы приложений.

В случае б) находим вероятность P₃₆(k ≥ 10) того, что рабо­тают более десяти приборов. Применяем для решения этой части задачи интегральную теорему Лапласа. Находим сначала значения x₁, x₂:

, /

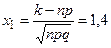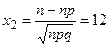Тогда искомая вероятность будет:

,

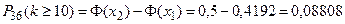Значения функции Лапласа 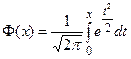взяты из таблицы приложений.

Пример 19. Всхожесть семян составляет в среднем 80%. Найти наивероятнейшее число всхожих семян среди девяти имеющихся в наличии.

Решение. Пусть А - событие, состоящее в том, что семя взойдет. Число k₀ определим с помощью двойного неравенства для определения наивероятнейшего числа. Поскольку n = 9, p= 0,8 и q = 0,2, то 9 · 0,8 - 0,2 < k ₀ < 9 · 0,8 + 0,8 = 8. Получены дна целых числа; значит, существует два наивероятнейших числа всхожих семян: 8 и 7. Вероятности их наибольшие и равны между собой. Действительно,

,

.

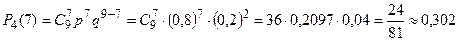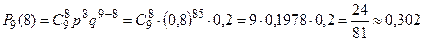Пример 20. Монета подброшена 10 раз. Найти вероятность того, что герб выпадет: а) от 4 до 6 раз; б) хотя бы один раз.

Решение. Пусть А - событие, состоящее в том, что выпадет герб. По условию задачи имеем: n =10, k₁ =4, k₂ =6, p=q=0,5. Находим а)

.

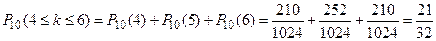б) Согласно формуле отыскания вероятности того, что собы­тие наступит хотя бы один раз

.

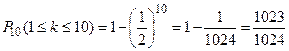Пример 21. В нерестовике содержится 200 рыб - произво­дителей вида А. Вероятность отдачи икры в искусственных условиях рыбы вида А равна 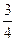. Требуется найти вероятность того, что

икру отдадут 150 рыб.

Решение. Вероятность того, что ровно 150 рыб из 200 отда­дут икру, найдем, используя локальную теорему Лапласа

, где .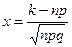

Значение функции φ(х) возьмем из таблицы. Находим:

п = 200, npq = 200 · 0,75 · 0,25 = 150 · 0,25 = 0,375.

т = к = пр = 150 .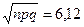

р = 0,75 .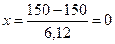

q = 0,25.

Получим: .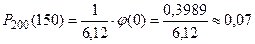

Пример 22. В партии из 400 деталей 80% - стандартных. Найти границы, в которых с вероятностью 0,9544 заключена доля стандартных деталей.

Решение. Воспользуемся формулой, являющейся частным случаем формулы Муавра-Лапласа

,

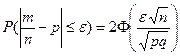где т/п - доля числа наступивших событий А в п испытаниях,

п - число испытаний,

р - вероятность наступления события А в одном испытании,

ε - величина отклонения доли т/п от вероятности р,

q = 1 - р - вероятность ненаступления события А в одном ис­пытании.

Для данной задачи А - событие, состоящее в том, что деталь стан­дартная, п = 400; р = 0,8; q =0,2; Р = 0,9544, величину ε нужно найти.

Итак: .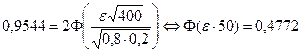

По таблице- приложений значений функции Лапласа Ф(х) находим, что ε · 50 = 2, следовательно, ε = 0,04. Таким образом, |m/n - 0,8| < 0,04 и 0,76 < т/п < 0,84.

Пример 23. Среднее число заявок, поступающих на пред­приятие бытового обслуживания за 1 час, равно трем. Найти веро­ятность того, что за 2 часа поступит 5 заявок. Предполагается, что поток заявок - простейший.

Решение. По условию λ = 3, t =2, k = 5. Воспользуемся формулой

.

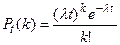Искомая вероятность того, что за 2 часа поступит 5 заявок, равна .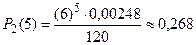

Пример 24. Среднее число заявок, поступающих на АТС в одну минуту, равно двум. Найти вероятности того, что за четыре минуты поступит:

а) три вызова;

б) менее трех вызовов;

в) не менее трех вызовов.

Решение, а) По условию λ = 3, t = 2, k=5. Воспользуемся фор­мулой: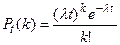

Подставив данные условия задачи, получим: .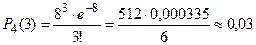
б) Найдем вероятность того, что за четыре минуты поступит менее трех вызовов, т.е. ни одного вызова, или один вызов, или два вызова. Поскольку эти события несовместны, применим теорему суммы несовместных событий:

.

в) Найдем вероятность того, что за четыре минуты поступит не менее трех вызовов: так как события «поступило менее трех вызовов» и «поступило не менее трех вызовов» - противоположные, то сумма вероятностей этих событий равна единице: Р₄(k < 3 ) + Р₄(k≥ 3 ) = 1.Поэтому .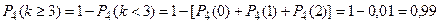

Дата добавления: 2014-11-20