Методические указания. Тема 4.1. Неопределенный интеграл

Тема 4.1. Неопределенный интеграл

Вопросы для самопроверки

1. Частные производные и полный дифференциал.

2. Производные от сложных функций.

3. Производные неявно заданных функций.

4. Касательная плоскость и нормаль к поверхности.

5. Геометрический смысл полного дифференциала.

6. Частные производные высших порядков.

7. Формула Тейлора для функции нескольких переменных.

8. Экстремум функции нескольких переменных.

9. Условный экстремум.

Раздел 4. Интегральное исчисление функций одной переменной

Учебники: [7, гл. 8], [9, гл. 6, 7], [16, гл. 13], [33, ч. 2, гл. 4, §§ 4.1-4.6].

Аудиторная работа: [3, №№ 1685, 1688, 1693, 1694, 1696, 1698, 1699, 1712, 1715, 1716, 1719, 1723, 1724, 1742, 1744, 1757, 1833, 1836, 1837, 1842, 1851, 1855, 1874, 1877, 1884, 2013, 2017, 2023, 2025, 2037, 2039, 2048, 2051, 2071, 2073, 2090, 2093, 2105, 2111, 2152, 2155], [7, гл. 8, №№ 5, 6, 7, 10, 12, 15, 16, 23, 27, 29, 33, 36, 40, 43, 51, 52, 56, 67, 71, 77, 78, 80, 90, 91, 92, 95, 102, 106, ПО, 113, 114, 118, 123, 124, 125, 147, 148, 153, 158, 162], [20, ч. 1, №№ 6.19, 6.23, 6.25, 6.27, 6.29, 6.43, 6.48, 6.65, 6.70, 6.79, 6.115, 6.117, 6.123, 6.125, 6.131, 6.133, 6.143, 6.153, 6.163, 6.172, 6.174, 6.191, 6.193, 6.195, 6.203, 6.219, 6.239, 6.245, 6.248, 6.253, 6.263], [33, №№ 34.1, 34.3, 34.5, 34.7, 34.9, 34.11, 35.1, 35.3, 35.5, 35.7, 35.9, 35.11, 36.1, 36.3, 36.5, 36.7, 36.9, 36.11, 37.1, 37.3, 37.5, 37.7, 37.9, 37.11, 38.1, 38.3, 38.5, 38.7, 38.9, 38.11, 39.1, 39.3, 39.5, 39.7, 39.9,39.11], [38, №№ 1.2.1 - 1.2.16,2.2.1 -2.2.16,3.2.1 -3.2.8,4.2.1 -4.2.12, 5.2.1-5.2.10].

Самостоятельная работа: [3, №№ 1686, 1689, 1690, 1695, 1697, 1700, 1713, 1717, 1720, 1725, 1726, 1737, 1745, 1768, 1834, 1838, 1841, 1853, 1860, 1876, 1881, 1885, 2012, 2016, 2027, 2028, 2038, 2041, 2050, 2069, 2074, 2091, 2095, 2110, 2112, 2153, 2154], [7, гл. 8, №№ 8, 11, 13, 14, 18, 20, 21, 25, 28, 30, 31, 34, 35, 41, 44, 45, 47, 53, 57, 61, 68, 69, 79, 81, 84, 87, 93, 94, 97, 99, 109, 112, 116, 119, 120, 121, 127, 146, 149, 150, 154, 159], [20, ч. 1, №№ 6.21, 6.26, 6.28, 6.40, 6.41, 6.56, 6.58, 6.64, 6.66, 6.72, 6.80, 6.116, 6.122, 6.124, 6.126, 6.130, 6.134, 6.136, 6.158, 6.168, 6.171, 6.175, 6.194, 6.196, 6.198, 6.202, 6.218, 6.240, 6.242, 6.246, 6.250, 6.256], [33, №№ 34.2, 34.4, 34.6, 34.8, 34.10, 34.12, 35.2, 35.4, 35.6, 35.8, 35.10, 35.12, 36.2, 36.4, 36.6, 36.8, 36.10, 36.12, 37.2, 37.4, 37.6, 37.8, 37.10, 37.12, 38.2, 38.4, 38.6, 38.8, 38.10, 38.12, 39.2, 39.4, 39.6, 39.8, 39.10, 39.12], [38, №№ 1.3.1 - 1.3.16, 2.3.1 - 2.3.16, 3.3.1 - 3.3.8, 4.3.1 - 4.3.12, 5.3.1-5.3.10].

Операция нахождения первообразной функции является обратной по отношению к операции дифференцирования функции. Поэтому перед изучением этой темы рекомендуется повторить таблицу производных элементарных функции и основные правила дифференцирования.

Определение. Пусть функция f(x) определена на интервале (a, b). Функция F(x) называется первообразной для функции f(x) на интервале (а, b), если F(x) определена и дифференцируема на интервале (а, b) и в каждой точке этого интервала F’(x) = f (x).

Таким образом, первообразная для f(x) — это такая функция, продифференцировав которую, получаем f(х).

Пример 4.1.1. Первообразной для функции f(x) = sinx на интервале 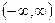является функция F(x) = – cos x, т.к. F'(x) = (–cos x)' = sin x = f(x).

Пример 4.1.2. Первообразной для функции 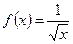на интервале 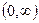является функция 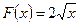, т.к. .

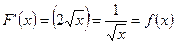При работе с первообразной интервал (a, b) обычно опускается.

Из определения первообразной следует, что если F(x) является первообразной для функции f(х), то F(x) + С при любой постоянной С также является первообразной для f(x). Важно отметить, что множество всех первообразных для функции f(x) исчерпывается множеством F(x) + С, где С ‑ произвольная постоянная.

Определение. Множество всех первообразных для функции f(x) называется неопределенным интегралом от функции f(x) и обозначается символом

.

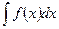Если F(x) — некоторая первообразная для функции f(x), то 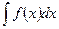вычисляется по формуле

.

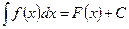где С — произвольная постоянная.

Пример 4.1.3. 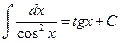, т.к. 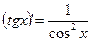, т.е. tg x является первообразной для функции .

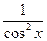Пример 4.1.4. 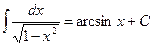, т.к. , т.е. 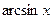является первообразной для функции .

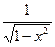Для освоения техники интегрирования необходимо четкое знание таблицы неопределенных интегралов и их основных свойств. Заметим, что таблица неопределенных интегралов представляет собой расширенную таблицу производных основных элементарных функций, в которой функции и их производные поменялись местами.

Приведем основные свойства неопределенного интеграла:

1. ;

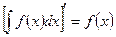2. ;

3. ;

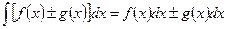4. .

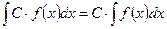Простейший прием интегрирования основан на свойствах 3,4 линейности неопределенного интеграла. Чтобы им воспользоваться, нужно представить подынтегральную функцию в виде линейной комбинации функций, имеющих табличные первообразные.

Пример 4.1.5. .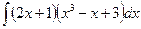

Раскрыв скобки в подынтегральной функции, ее можно представить в виде линейной комбинации степенных функций, интегралы от которых являются табличными. Поэтому

.

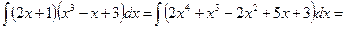
Линейная комбинация табличных интегралов часто получается путем почленного деления числителя подынтегральной функции на знаменатель и использования свойств линейности неопределенного интеграла.

Пример 4.1.6.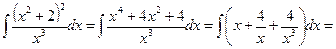

.

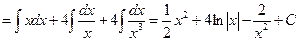Пример 4.1.7.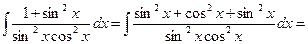

.

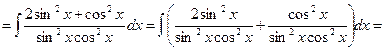
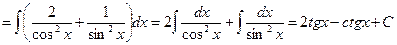Остановимся на основных методах интегрирования неопределенного интеграла.

Дата добавления: 2014-11-20