Дифференциальные операции над векторными полями

Скалярные и векторные поля

Тема 6.5. Элементы векторного анализа

Литература: [3, №№4401 – 4404; 6, гл. 6, §§ 1 – 2; 20, гл.2, §§ 1 - 6].

Пусть Ω - область в трехмерном пространстве. Скалярным полем на Ω называют числовую функцию u(M), заданную на точках MєΩ. Векторным полем на Ω называют векторную функцию а(М), заданную на точках MєΩ.

Если в пространстве введена декартова система координат, то скалярное поле или векторное поле а(М) на Ω становится функциями координат точек: u(x;y;z), a(x;y;z) = (a_x(x;y;z); a_y(x;y;z); a_z(x;y;z)).

При выборе другой декартовой системы координат меняются координаты точек М(x;y;z) на М(x;y;z).

Множество точек поля М, заданное уравнением u(x;y;z)=const, называется поверхностью уровня скалярного поля u.

Векторной, или силовой линией векторного поля а называют гладкую кривую, которая в каждой своей точке М касается вектора поля а(М). Если r=(x;y;z) - радиус-вектор переменной векторной линии поля a=(a_x;a_y;a_z), то

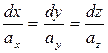(6.5.1)

- дифференциальное уравнение силовых (векторных) линий.

Пусть γ – плоская кусочно-глакая простая замкнутая кривая, нигде не касающаяся векторных линий поля а. Поверхность, образованную векторными линиями, пересекающими γ, называют векторной трубкой поля а.

Оператор

Литература: [3, №№3439 – 3448, 4405-4429; 5, §3.4; 6, гл.6, §§ 5 – 6; 20, гл.2, §§ 12, 13].

Векторный дифференциальный символ называют «набла» по обозначающей его букве, а также оператором Гамильтона. В декартовой системе координат

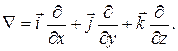(6.5.2)

Градиентом дифференцируемого на Ω скалярного поля u в точке MєΩ называют вектор, обозначаемый grad u или u и задаваемый в декартовой системе координат формулой

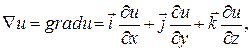(6.5.3)

где производные поля вычислены в точке М(x;y;z).

Для производной поля и в точке М(х; у; z) по направлению произволь­ного единичного вектора l существует формула

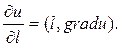(6.5.4)

Градиент поля в точке М направлен по нормали к поверхности уровня, проходящей через М, в сторону возрастания поля, и его модуль |gradu| ≡ | u| равен наибольшей производной по направлению в этой точке.

Дивергенцией, или расходимостью дифференцируемого на Ω поля а в точке MєΩ называют число, обозначаемое div а или (,a) и задаваемое в декартовой системе координат формулой

(6.5.3)

где а = (а_х; а_у; a_z) и производные вычислены в точке М(х; у; z).

Значение числовой функции div а в точках Ω не зависит от выбора де­картовой системы координат, то есть div a - скалярное поле на Ω.

Ротором (вихрем, или ротацией) дифференцируемого на Ω. векторного поля а в точке MєΩ называют вектор, обозначаемый rot а, или [ ,a] (ино­гда х а) и задаваемый формулой

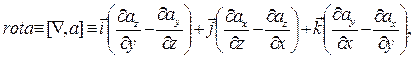(6.5.6)

где а = (а_х; а_у; a_z) и производные вычисляются в точке М(х; у; z).

Значение векторной числовой функции rot а в точках Ω не зависит от выбора декартовой системы координат одинаковой ориентации, но rot а ме­няет знак при смене ориентации системы координат.

Для записи rot а в декартовой системе координат используют такой же символический определитель, как и для векторного произведения векторов:

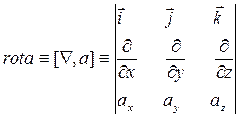(6.5.7)

Формулы (6.5.3), (6.5.5) и (6.5.6) определяют над скалярными и вектор­ными полями три основные дифференциальные операции первого порядка - действие на скаляр и вектор. Для этих операций используются такие же обозначения, как и для произведения вектора на скаляр или вектор, и обла­дают эти операции такими же свойствами, как и эти произведения. Но по­следнее - с учетом, во-первых, невозможности перестановки символа с этим скаляром или вектором, на который он действует, и, во-вторых, диффе­ренциального характера символа .

Операции (6.5.3), (6.5.5) и (6.5.6) - линейны.

Пусть скалярное поле и, а также векторные поля а и b дифференцируе­мы на Ω, с - постоянный вектор, тогда:

1. div(ua) = (gradu,a) + udiva. (6.5.8)

2. div[a, b] = (b, rota) - (a, rotb). (6.5.9)

3. rot[c,a] = с diva - (c, grad)a. (6.5.10)

Символ может встречаться в выражениях не раз, создавая дифференциальные символы второго и более высоких порядков:

4. 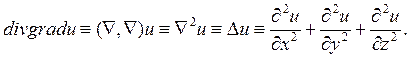(6.5.11)

- оператор Лапласа.

Символ [ , ], как нетрудно проверить, нулевой, что естественно с точки зрения векторной алгебры. Поэтому:

5. rot gradu = [ , Vu] = [ , ]u = 0. (6.5.12)

6. div rota = (,[ ,a]) = ([ , ]a) = 0. (6.5.13)

Дата добавления: 2014-11-20