Алгебраические критерии устойчивости

Алгебраические критерии устойчивости позволяют судить об устойчивости системы по коэффициентам характеристичес­кого уравнения.

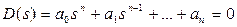. (3.37)

Из алгебраических критериев устойчивости наиболее ши­рокое распространение получили критерии устойчивости Ра­уса и Гурвица.

Прежде чем познакомиться с ними, заметим, что необходи­мым условиемустойчивостисистемы любого порядка является положительность всех коэффициентов характеристического уравнения (3.37):

a₀ > 0; a₁> 0; … a_n > 0. (3.38)

Действительно, в соответствии с теоремой Безу уравнение (3.37) можно представить в виде произведения множителей, содержащих корни s_l, s₂,…s_n:

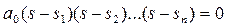. (3.39)

Если все корни характеристического уравнения будут от­рицательны, то все множители выражения (3.39) будут иметь вид

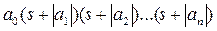, (3.40)

где 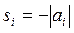— значения корней.

Производя перемножение в (3.40), получим (3.37), в кото­ром все коэффициенты будут определяться положительными членами |а_i| выражения (3.40), т. е. будут положительны.

Если характеристическое уравнение (3.37) имеет комплекс­ные корни с отрицательными вещественными частями, то оно может быть представлено в виде

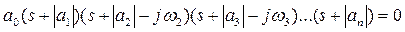(3.41)

или

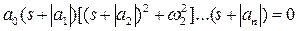(3.42)

Уравнение (3.42) также приводится к виду уравнения (3.37) с положительными коэффициентами.

Для систем первого и второго порядков необходимое условие устойчивости является и достаточным условием устойчиво­сти, поскольку в этом случае при положительных коэффи­циентах характеристического уравнения все его корни явля­ются левыми. Однако для систем третьего и высших порядков положительность коэффициентов характеристического урав­нения является необходимым условием устойчивости, но не достаточным. В этом случае все вещественные корни характе­ристического уравнения (если они есть) левые, комплексные же корни могут быть и правыми.

Критерии устойчивости Рауса и Гурвица позволяют по коэффициентам характеристического уравнения (3.37) без вы­числения его корней сделать вывод об устойчивости системы.

3.5.1. Критерий устойчивости Рауса.

Этот критерий устойчиво­сти был в 1877 г. предложен английским математиком Э. Рау­сом в виде некоторого правила (алгоритма), которое наиболее просто поясняется таблицей 1.

Таблица 1. Таблица Рау­са

В первой строке табл.1 записывают в порядке возраста­ния индексов коэффициенты характеристического уравнения (3.37), имеющие четный индекс: а₀, а₂, а₄, а₆,...; во второй строке — коэффициенты (3.37) с нечетным индексом: a_l a₃, а₅,....

Любой из остальных коэффициентов таблицы определяют как

(3.43)

где

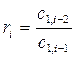(3.44)

В (3.43) и (3.44) k — индекс, означающий номер столбца табл.1; i — индекс, означающий номер строки табл.1.

Число строк таблиц Рауса равно степени ха­рактеристического уравнения плюс единица: (n+ 1).

После того как таблица Рауса заполнена, по ней можно су­дить об устойчивости системы. Условие устойчивости Рауса формулируется так: для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса имели один и тот же знак, т. е. при 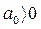были положительными:

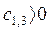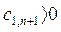; ; ; … (3.45)

Если не все коэффициенты первого столбца положительны, то система неустойчива, а число правых корней характерис­тического уравнения равно числу перемен знака в первом столбце таблицы Рауса.

Критерий Рауса особенно удобен, когда заданы числовые значения коэффициентов характеристического уравнения (1). В этом случае определение устойчивости можно выпол­нить довольно быстро даже при характеристических уравне­ниях высокого порядка.

Форма алгоритма, с помощью которого составляют таблицу Рауса, очень удобна для программирования, поэтому критерий Рауса нашел широкое применение при исследова­нии влияния на устойчивость либо коэффициентов характерис­тического уравнения, либо отдельных параметров системы, не очень сложным образом входящих в эти коэффициенты.

Дата добавления: 2014-11-20