
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вопрос 15. Основные группы болезней кости
|
|
|
|
Основные группы болезней кости
Общепринятой классификацией болезней костей нет. В нашей стране наиболее распространенной является классификация, в основу которой положены этиологический и патогенетический принципы. В классификации приведены сходные по морфологии группы патологических процессов без перечисления отдельных нозологических форм. Различают следующие группы болезней костей: травматические, воспалительные, дистрофические и диспластические.
Травматические болезни (или повреждения) костей – одна из самых многочисленных групп патологии костей: переломы, травматические артрозы, деформирующий спондилез и др.
Воспалительные заболевания костей вызываются стрептококками и стафилококками. Это так называемые неспецифические воспалительные заболевания (остеомиелит, остит и др.). Различают также специфические воспалительные заболевания костей (в том числе остеомиелит), которые встречаются при туберкулезе, сифилисе, бруцеллезе и др.
Неспецифический остеомиелит возникает либо гематогенно (возбудитель в крови), либо путем распространения воспаления на кость из других органов и тканей, либо в результате экзогенного инфицирования кости при наличии раны.
Дистрофические заболевания костей (остеохондропатии) характеризуются местным нарушением кровообращения кости и появлением участков асептического некроза в губчатом веществе кости.
Такие болезни костей возникают под влиянием токсических поражений (фосфорные, фтористые и другие отравления), в результате алиментарных расстройств (цинга, рахит и др.), при эндокринных заболеваниях (пара-тиреоидная остеодистрофия и др.)
Диспластические заболевания костей – это недостаточное или избыточное развитие костей, в том числе гигантизм, пороки развития хрящевой ткани, остеосклероз.
|
|
|
К этой же группе болезней относятся опухоли костей – доброкачественные (остеома, хондрома и др.) и злокачественные (первичные – остеогенная саркома и др.; вторичные – метастатические).
Системы линейных уравнений с n-переменными.
Системы m-линейных уравнений с n-независимыми имеет вид
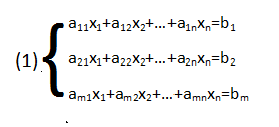
Где aij-это коэффициент при неизвестных, а bi-это свободные члены или равные части уравнения
Систему (1) можно кратко записать в виде
 ijxj= bi, i=
ijxj= bi, i= 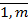 (2)
(2)
Решением системы (1) наз-ся совокупность n-чисел x1,x2,…, xn при подстановке которой в систему (1) каждое уравнение обращается в верное равенство. Система уравнений называется совместной, если она имеет решение и несовместной, если не имеет решений.
Совместная система наз-ся определенной, если она имеет единственное решение и неопределённой, если она имеет более одного решения.
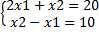 совместная и определенная, т.к. имеет ед. решение (10;0)
совместная и определенная, т.к. имеет ед. решение (10;0)
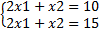 несовместимая
несовместимая
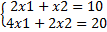 совместная, но не определенная
совместная, но не определенная
Две системы ур-ний равносильными или эквивалентными, если они имеют одно и то же множество решений.
Запишем систему (1) в матричной форме.
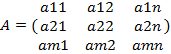 , B= (
, B= (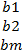 )
)
Где A-матрица коэф. при неизвестных
В-матрица столбец свободных членов.
Тогда систему (1) можно записать Ax=B (3)
Система m-линейных уравнений с n-переменными. Там же, метод обратной матрицы Вопрос 16. Пусть число уравнений системы (1) равно числу переменных m=n, тогда матрица системы является квадратной, а ее определитель ∆=|A|называется определителем системы.
Рассмотрим решение системы двух уравнений с двумя неизвестными.
(4) 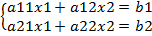 | исключим переменную x2, умножив 1 ур-е на а22 второе-на (-а21) и сложить.
| исключим переменную x2, умножив 1 ур-е на а22 второе-на (-а21) и сложить.
Исключим переменную х1, умножив 1ур-е (-а21), 2 ур-е-на а11 и сложить
В результате получим систему
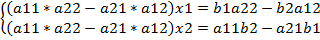 (5)
(5)
Выражение в скобках есть определитель
∆1=a11a22-a21a12=_ 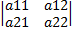 +
+
|
|
|
∆2=a11b2-a21b1=_ 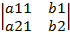 +
+
(6) 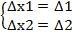
Из полученной системы следует, что если определитель системы ∆ отличен от нуля, то система (4) имеет единственное решение опред-е по формуле x1=  , x2=
, x2= 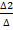
Частные случаи:
1)Если ∆=0, ∆1≠0, или ∆2≠0, то система (4) несовместная
2)Если ∆=∆1=∆2=0, то система (4) неопределенная, имеет бесчисленное множество решений.
Для получения решения системы (1) при m=n в общем виде методом обратной матрицы предположим, что квадратная матрица системы 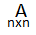 –невырожденная, т.е. ее определитель |A|≠0. В этом случае сущ-т обратная матрица А-1. Умножая обе части матрицы равенства АХ=В на А-1 получим А-1(АХ)=А-1В. Т.к. по определению обратной матрицы
–невырожденная, т.е. ее определитель |A|≠0. В этом случае сущ-т обратная матрица А-1. Умножая обе части матрицы равенства АХ=В на А-1 получим А-1(АХ)=А-1В. Т.к. по определению обратной матрицы
А-1(АХ)= АА-1Х=ЕХ=Е, то решением системы методом обратной матрицы будет матрица столбец
Х=А-1В (7)
Вопрос 17. Правило Крамера.
Теорема. Пусть ∆-определитель матрицы А(∆=|A|), ∆j-определитель матрицы, получаемой из матрицы А с заменой j-го столбца столбцом из свободных членов. Тогда при ∆≠0 система имеет единственное решение, опр-е по формулам
xj= 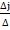 (8), j=
(8), j= 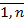
Формулами Крамера наз-ся формула (8)
Доказательство:
A-1= 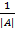 *
*  , где
, где  -присоединенная матрица.
-присоединенная матрица.
Т.к. элементы  есть алгебраические дополнения элементов матрицы AI транспонированной к A, то запишем равенство Х=А-1В (7) в развернутом виде
есть алгебраические дополнения элементов матрицы AI транспонированной к A, то запишем равенство Х=А-1В (7) в развернутом виде
( )=
)= 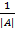 (
( )*(
)*(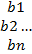 )
)
Т.к. |A|= ∆ после умножения матриц получим (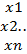 )=
)=  (
(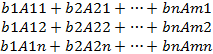 )
)
Отсюда следует, что любого j=1,n
xj=  (b1Aij+b2A2j+…+bnAnj)
(b1Aij+b2A2j+…+bnAnj)
b1Aij+b2A2j+…+bnAnj =∆j, где j –определитель матрицы, полученной из матрицы A с заменой j-го столбца столбцом из свободных членов
Xj= 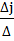 .
.
Вопрос 21. Деление отрезка в данном отношении.
Пусть на плоскости задан М1М2.
И пусть М-любая точка этого отрезка, не совпадающая с концами
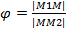 (4)
(4)
λ- отношение в котором точка М делит отрезок М1М2.
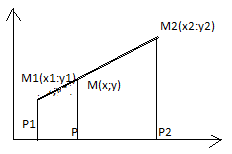
Задача о делении отрезка в данном отношении состоит в том, что по данному отношению λ и данным координатам М1 и М2 находятся координаты точки М
Теорема. Если точка М от (х;у) делит отрезок М1М2 в отношении λ, то координаты этой точки
y m:val="p"/></m:rPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math" w:cs="Calibri"/><wx:font wx:val="Cambria Math"/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>О»</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 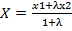 , y m:val="p"/></m:rPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math" w:cs="Calibri"/><wx:font wx:val="Cambria Math"/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>О»</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
, y m:val="p"/></m:rPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math" w:cs="Calibri"/><wx:font wx:val="Cambria Math"/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>О»</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 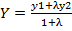 (5)
(5)
|
|
|
Доказательство:
Опустим перпендикуляр из точки М1, М и М2. Обозначим через Р1, Р, Р2-основания этих перпендикуляров. На основе теории о пропорц. отрез. прямой заключается между параллельными прямыми:
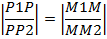
|P1P|=|X-X2|, |P-P2|=|X2-X|
Т.к. значение под модулем одинакового знака, то можно записать
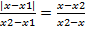 =>
=>  => x=
=> x= 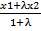
Получить 2-ю из (5) аналогично, спроектировать координаты точки на ось у.
Если М-середина отрезка М1М2, то λ=1 и по формулам (5) координаты отрезка находятся формулой (5).
Вопрос 22. Полярная система координат.
Состоит их точки О(полюс) и исходящего из него луча ОЕ(полярный курс). Пусть М-производная точка плоскости, -расстояние точки М от О, ϕ-угол, на коэф. которого нужно поверн. полярн. ось.
Установим связь между полярными координатами точки М(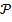 ;у) и (х;у).
;у) и (х;у).
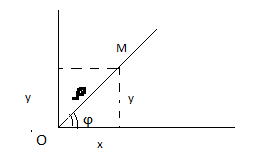
При этом будем предполагать, что начало координат нах-ся в полюсе, а полож. Ось абсцисс совпадает с полярной осью.
Пусть М имеет прямоугольн. коорд. ху М(ху) и поляр. коорд. М(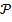 ; ϕ)
; ϕ)
Из чертежа:
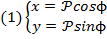
 о рмулы (1) выражают прямоугол. Коорд. Через полярн.
о рмулы (1) выражают прямоугол. Коорд. Через полярн.
Или выраж. пол. коорд. через тр-гольн. форм. 1
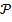 =√x22+y22 tg ϕ=
=√x22+y22 tg ϕ=  (7)
(7)
Заметим, что tg ϕ определяет два значения половины угла ϕ, т.к. ϕ меняется от 0 до ∏. Из этих 2-х значений … правило, которое выполняет равенство (1)
Вопрос 23. Уравнение прямой с угловым коэффициентом.
Уравнение F(x;y)=0, называется уравнение линейной L, заданной в системе координат. Если ему удовл-т координаты изображаемой точки, лежащей на линии L и не удовлетворяют координаты точки не лежащей на этой линии. Линия L может опред. ур-м вида F(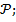 ϕ)=0.
ϕ)=0. 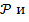 ϕ- полярные координаты точки.
ϕ- полярные координаты точки.
|
|
|
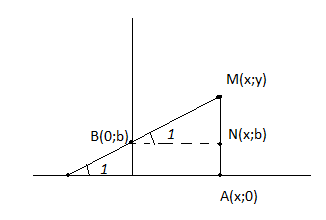 1=
1= 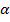
Пусть прямая пересекает ось ОУ. В точке В с координатами 0 и b B(0;b) и образует с осью ОХ угол 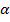 : 0<
: 0< 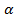 <∏/2
<∏/2
Возьмем на прямой произвольную точку М с координатами (х;у), тогда tg 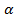 -угол наклона прямой tg
-угол наклона прямой tg 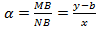 (1)
(1)
Введем угловой коэффициент k= tg 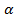
k=  => y=kx+b (2)
=> y=kx+b (2)
Справедливо при условии ∏/2< 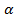 <∏ ур-е прямой с углов. коэффициентом.
<∏ ур-е прямой с углов. коэффициентом.
Рассмотрим частные случаи:
1.b=0 => y=kx-проход ч/з начало координат и образующей
При k= tg 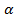 >0-острый угол с ОХ
>0-острый угол с ОХ
При k<0- тупой угол
y=x-биссектриса 1-го и 3-го коорд. углов
y=-x-биссектриса 2-го и 4-го координатных углов
2.Если 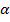 =∏/2, то прямая перпендикулярна оси ОХ и k= tg
=∏/2, то прямая перпендикулярна оси ОХ и k= tg 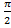 -не сущ-т, т.е. вертикальная прямая не имеет углового коэффициента.
-не сущ-т, т.е. вертикальная прямая не имеет углового коэффициента.
3.Если 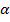 =0, то k=tg0=0. Отсюда y=b-прямая параллельная оси OX.
=0, то k=tg0=0. Отсюда y=b-прямая параллельная оси OX.
Если прямая отсекает от OX, то ее уравнение будет x=a. А уравнение OY=X=0
Вопрос 24. Уравнение прямой, проходящей через данную точку в заданном направлении. Уравнение прямой, проходящей через две данные точки.
1) Пусть прямая проходит M1(x1;y1) и образует с осью OX угол x≠ 
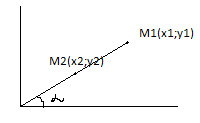
Т.к. М1 лежит на прямой, то ее координаты удовлетворяют ур-ю
y1= kx1+b (3)
Вычитая (3) из (2) y=kx+b получаем уравнение искомой прямой
y-y1 =k(x-x1) (4)
Если прямая проход. М1 перпендикулярна ОХ, то ее углов. коэф-т равен бесконечности, и ее уравнение имеет вид x-x1=0
2) Пусть даны точки М1 и М2
Запишем уравнение М1М2 в виде, где k-пост. Неизвестная углового коэф-та.
Т.к. прямая М1М2 проходит ч/з М1 ее координаты уд-т ур-ю(4)
y2-y1=k(x2-x1)
Отсюда вместо k подставим в 4 получим
y-y1= 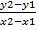 (x-x1)
(x-x1)
Если y1≠y2, то ур-е можно переписать
 (5)
(5)
Если y1=y2, то ур-е искомой прямой имеет вид:
y1=y2 => y=y1, в этом случае прямая параллельна ОХ
x1=x2, то прямая, проходящей точки имеет вид x1=x
Вопрос 25. Угол между прямыми. Условия параллельности и перпендикулярности прямых.
1. y=k1x+b1
y=k2x+b2, где k1=tg 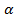 1, k2=tg
1, k2=tg 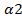
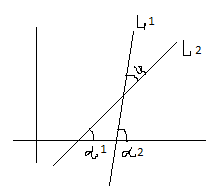
Из геомет. рассмотр.
y= 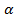 2-
2- 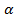 1, tgϕ=tg(
1, tgϕ=tg(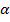 2-
2- 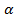 1)=
1)= 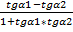 или tg
или tg 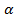 =
= 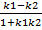 (6)
(6)
Формула (6) определяет один из углов между прямыми, а другой угол равен ∏-ϕ
2. Условия параллельности и перпендикулярности.
Если прямы L1 и L2-параллельны, то ϕ=0
k2-k=0 => k1=k2
Условия параллельности двух прямых является равенство их угловых коэффициентов.
Если L1 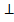 L2, то ϕ=
L2, то ϕ= 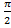 . Отсюда
. Отсюда 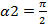 --
-- 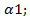 tg
tg 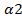 = tg(
= tg( 1)= -- ctg
1)= -- ctg 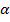 1= -
1= - 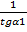
k2= -- 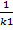
Условия 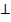 -ти 2-х прямых состоит в том, что их коэф. обратны по величине и общ. по знаку.
-ти 2-х прямых состоит в том, что их коэф. обратны по величине и общ. по знаку.
Вопрос 26. Общее уравнение прямой. Уравнение прямой в отрезках на осях.
1. Теорема:
В прямоугольной системе координат любой прямой задает уравнение 1-й степени
Ax+By+C=0
При любых А, В, С, где А, В не были нулями оба сразу, представляет прямую линию. Всякую прямую можно представить уравнением этого вида. Поэтому его называют общим уравнением прямой.
Док-во: Пусть В≠0, тогда ур-е можно записать в виде y = -  x -
x - 
1.Если А≠0, С  ≠0, получим y=kx+b
≠0, получим y=kx+b
Если А≠0, С=0, y=kx-ур-е прямой, проходящей через начало координат.
Если А=0, С≠0, то y=b – прямая параллельна ОХ
Если А=0, С=0, то y=0 – ось OX
2.B=0, A≠0, тогда ур-е (7) примет x= --  ; ур-е прямой параллельной ОУ, а если С=0, то х=0 – ось ОУ.
; ур-е прямой параллельной ОУ, а если С=0, то х=0 – ось ОУ.
Т.к. при любом значении А и В не равны одновременно 0, ур-е (7)-есть ур-е нек. прямой на плоскости ХОУ.
Линия определенная в прямоугольной системе координат ур-я 1-й степени- линия первого порядка.
2. Найдем уравнение прямой по заданным отрезкам а≠0, b≠0 от … на осях координат. Воспользуемся формулой прямой ч/з 2 заданные точки.
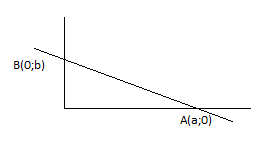
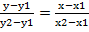
Подставим координаты точек в уравнение
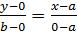 или r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
или r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 
Это ур-е наз-ся уравнением прямой в отрезках.
Вопрос 27. Нормально уравнение прямой. Расстояние от точки для прямой.
Пусть дана некоторая прямая L. Проведем ч/з начало координат прямую, перпендикулярную L и назовем ее нормалью. На нормали ведем направление от 0 к N, т.е. нормаль станет осью.
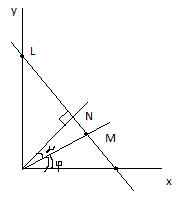
Обозначим ч/з α-угол на кот. нужно повернуть против часовой стрелки ось ОХ до совмещения положения напр. нормалями. p=ON. Выведем ур-е прямой L считая неизвест. число α и ρ:
Для этого возьмем на прямой L произвольную точку М с полярными координатами ρ и ϕ, где О-полюс, а ОХ-полярная ось.
Если точки O и N –не совпадают, то из тр-ка ONM находим
P= ρcos(α-ϕ)= ρ(cosαcosϕ+sinαsinϕ) или ρ*cosϕcosα+ ρ* sinϕsinα-P=0 (1)
Ур-е (1) есть ур-е прямой L в полярн. коорд……………………………………..
x=ρ*cosϕ, y=ρ*sinϕ
x*cosα+y*sinα-ρ=0 (2)
Если точки O и N cовпадают, то уравнение P=0 и уравнение принимает вид
x*cosα+y*sinα=0
Уравнение (2)- нормальное уравнение прямой L. Для того, чтобы привести общее уравнение прямой к нормальному виду (2) нужно все члены ур-я умножить на нормир. множитель μ.
Ax+By+C=0 (*)
μ = 
Перепишем
μA=cosα, μB=sinα, μC= -p
Знак интегрирующего множителя берется противоположно знаку С. Если прямая L задана ур-м (2), а точка М0(х0;у0)-не лежит на этой прямой, то расстояние от точки до прямой определяется как выражение
d=|x0cosα+y0sinα-p| (3)
Пусть даны М0(х0;у0) и прямая L ур-м *
Под расстоянием от точки М0до прямой L понимается длина перпендикуляра d=M0N, опущенного из точки М0 на прямую.
Для определения расстояния d необходимо:
1. Составить уравнение прямой M0N, перпендикулярной L проходящей ч-з точку М0.
2. Найти точку N (x;y)—пересечение прямых решив совместно ур-я M0N и L/
3. Найти расстояние по формуле
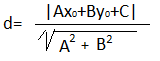
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 414; Нарушение авторских прав?; Мы поможем в написании вашей работы!