Астатические системы

Амплитудно-фазовые характеристики разомкнутых стати­ческих систем автоматического управления при изменение час­тоты ω от—∞ до ∞ образуют замкнутый контур. У астати­ческих разомкнутых систем, которые содержат интегрирующие звенья, амплитудно-фазовые характеристики не образуют зам­кнутого контура. Для таких систем характеристическое урав­нение разомкнутой системы имеет корни, равные нулю, и мо­жет быть записано в виде

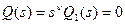, (3.117)

где ν — порядок астатизма; Q₁(s) — полином, не имеющий кор­ней, равных нулю.

Частотная передаточная функция разомкнутой астатичес­кой системы, содержащей интегрирующие звенья,

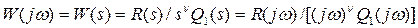(3.118)

При ω = 0 частотная передаточная функция астатической системы обращается в ∞, а ее амплитудно-фазовая характе­ристика претерпевает разрыв. Поэтому в этом случае трудно решить вопрос об устойчивости замкнутой системы, так как неясно, охватывает ли амплитудно-фазовая характеристика W(jω) точку (—1, j0).

Векторы jω при изменении частоты ω от — ∞ до ∞ из­меняют при переходе через начало координат фазовый угол скачком с — π/2 до π/2, но в каком направлении происходит их поворот в момент перехода через начало координат, сказать невозможно. Чтобы освободиться от этой неопределенности, идя по мнимой оси при изменении частоты от— ∞ до ∞, обходят начало координат в плоскости корней справа по полу­окружности бесконечно малого радиуса r (рис. 3.17), т. е. счи­тают не s = 0, a 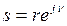(r → 0, — π/2 ≤ γ ≤ π/2).

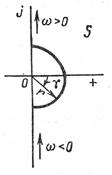
Рис. 3.17. Направление обхода особой точки.

Тогда все нулевые корни дадут точно такой же угол поворо­та, как левые корни, т. е. каждый из векторов повернется на π, и формулы (3.84) и (3.85)

из раздела 3.6 сохраняют свою силу.

Обходу начала координат по малой дуге 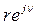в плоскости корней соответствует передаточная функция разомкнутой си­стемы

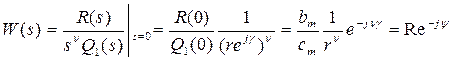, (3.119)

где b_m и с_m — свободные члены полиномов R(s) и Q₁(s).

При r → 0 модуль R → ∞, а аргумент ψ меняется от νπ/2 до — νπ/2 при изменении γ от — π/2 до π/2. Таким образом, во время движения по полуокружности бесконечно малого ра­диуса в плоскости корней частотная передаточная функция разомкнутой системы W(jω) может быть представлена в виде вектора бесконечно большой длины, поворачивающегося на комплексной плоскости по часовой стрелке на угол, равный — νπ (от νπ/2 до — νπ/2).

При изменении ω от 0 до ∞, т. е. при r → 0 и 0 ≤ γ ≤ π/2, частотная передаточная функция W(jω) будет изменяться по дуге бесконечно большого радиуса, описывая угол от 0 до — νπ/2. На рис. 3.18 показана амплитудно-фазовая характеристика разомкнутой аста­тической системы с астатизмом первого порядка ν = 1.

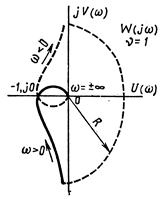
Рис. 3.18. А.Ф.Х. разомкнутой аста­тической системы с астатизмом первого порядка.

На основе сказанного выше для определения ус­тойчивости систем с аста-тизмом любого порядка 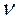достаточно построить одну ветвь амплитудно-фа­зовой характеристики ра­зомкнутой системы, соот­ветствующую положитель­ным частотам, дополнить ее дугой — νπ/2 окружно­сти бесконечно большого радиуса и затем приме­нить критерий устойчи­вости Найквиста.

Например, ра­зомкнутая астатическая система неустойчива.

Замкнутая система будет устойчива, если при изменении частоты ω от 0 до ∞ амплитудно-фазовая характерис­тика разомкнутой астатической системы W (jω), дополненная дугой — νπ/2 бесконечно большого радиуса, охватит точку (—1, j0) в положительном направлении 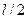, раз, где l — число правых корней характеристического уравнения разомкнутой системы.

Пример На рис. 3.19 приведена амплитудно-фазовая характеристика разомкнутой системы с астатизмом второго порядка ν = 2.

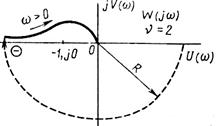
Рис. 3.19. А.Ф.Х. разомкнутой аста­тической системы с астатизмом второго порядка.

Замкнутая система в этом случае будет неустойчива, так как амплитудно-фазовая характеристика W(jω), дополненная ду­гой — νπ/2 — π бесконечно большого радиуса, всегда ох­ватывает точку (—1, j0) в отрицательном направлении (по часовой стрелке).

Пример. На рис. 3.20 приведена амплитудно-фазовая характерис­тика разомкнутой системы с астатизмом второго порядка, кото­рая после дополнения ее дугой — νπ/2 = — πбесконечно большого радиуса не охватывает точку (—1, j0) (число положи­тельных и отрицательных переходов через отрезок (—∞, —1) равно нулю).

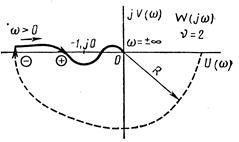
Рис. 3.20. А.Ф.Х. разомкнутой системы с дугой бесконечно большого радиуса

Следовательно, замкнутая система будет устой­чива.

Одним из достоинств критерия Найквиста является то, что он может быть применен и в тех практически важных случаях, когда неизвестны уравнения некоторых звеньев системы либо даже неизвестно уравнение всей разомкнутой системы в целом, но амплитудно-фазовая характеристика разомкнутой системы может быть получена экспериментально. Кроме того, крите­рий Найквиста позволяет до­вольно просто исследовать устойчивость систем с запаздыва­нием.

Дата добавления: 2014-11-20