
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры выполнения заданий. 1.Найдите суперпозицию функций для формулы: B ~ Ø(A Ú B) ® A
|
|
|
|
1.Найдите суперпозицию функций для формулы: B ~ Ø(A Ú B) ® A
Решение: определим порядок выполнения операций и запишем их с помощью элементарных функций от одной или двух переменных:
g3(в)=B;
g3(a)=A;
f9(а, в)= Ø(A Ú B);
f 12 (a, b)= Ø(A Ú B) ® A
Получаем: f10(g3( в), f12(f9(а, в), g3(a))).
2. Постройте канонические формы для функции  & b Å
& b Å  .
.
| a b |  & b & b
|  & b Å & b Å  . .
|
| 0 0 | 1 0 0 | 0 1 1 |
| 0 1 | 1 1 1 | 1 1 0 |
| 1 0 | 0 0 0 | 0 1 1 |
| 1 1 | 0 0 1 | 0 0 0 |
СДНФ =  &
&  Ú
Ú  & b Ú a &
& b Ú a &  º
º  & (
& ( Ú b) Ú a &
Ú b) Ú a &  º
º  & 1Ú a &
& 1Ú a &  º
º
º  Ú a &
Ú a &  º (
º (  Ú a) & (
Ú a) & (  Ú
Ú  ) º 1 & (
) º 1 & (  Ú
Ú  ) º
) º  Ú
Ú  .
.
СКНФ =  Ú
Ú  .
.
СПНФ =  Ú
Ú  =(1 + а) + (1 + b).
=(1 + а) + (1 + b).
3. С помощью теоремы о полноте установите полноту алгебры Жегалкина {Å, 1, *}:
Решение: представим функции алгебры логики через алгебру Жегалкина. Для этого воспользуемся дизъюнктивной формой:
a Å b = a ×  +
+  × b;
× b;
a = 0 +  = 0 × a + 1 ×
= 0 × a + 1 ×  = a Å 1;
= a Å 1;
a + b =  = ((
= ((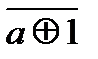 )(bÅ1))Å1.
)(bÅ1))Å1.
Задания для самостоятельного выполнения
1. Найдите суперпозицию функций для формул:
| 0) A&B ® BÚ A ¯ ØB 1) ØB Å A & B ® A | B 2) Ø(A & B)¯ Ø AÚ B ¯ A 3) Ø(A Ú B & A ~ B ¯ A) 4) B & ØA Ú Ø B Å A | B | 5) A ~ B | ØAÅ B ® A 6) B Ú A ¯ B Å ØA & B 7) Ø(B & A Ú Ø B) ® A¯ B 8) A & B Å Ø(A Ú B) ¯ A 9) B ~ A Å B & A | ØB |
2. Постройте канонические формы для функций:
0)  Å b Å Å b Å  ;
1)(а Ú ;
1)(а Ú 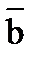 ) & (b Ú ) & (b Ú  );
2)(а → );
2)(а → 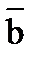 ) → с;
3)а & b Ú ) → с;
3)а & b Ú  & & 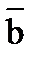 ;
4)(а → b) → (a → с); ;
4)(а → b) → (a → с);
| 5)  & &  ;
6) ;
6)   ;
7)а & b Ú ;
7)а & b Ú 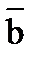 → с;
8)(a Å b) & → с;
8)(a Å b) &  ;
9)( ;
9)( → → 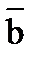 ) Å с; ) Å с;
| |||
| a b с | ||||
|
|
|
СДНФ =
СКНФ =
СПНФ=
3. С помощью теоремы о полноте установите полноту системы:
| 0) {Å, 1}; 1) {Ø®, 1}; 2) {®, Å}; 3) {®, 0}; 4) штрих Шеффера; | 5) {®, 1}; 6) стрелка Пирса; 7) {Å, 1}; 8) {®, 0}; 9) {®, Å}; |
4. Булевская функция f(x, y, z) задана таблично. Представьте эту же функцию формулой логики и функциональной схемой:
| Переменные | Варианты задания функции f(x, y, z) | |||||||||||
| x | y | z | 0) | 1) | 2) | 3) | 4) | 5) | 6) | 7) | 8) | 9) |
Практическое занятие №9. Применение
алгебры логики
| Цель работы: | 1. | изучить способы минимизации булевых функций в классе ДНФ; |
| 2. | получить навыки в применении булевых функций для анализа и синтеза дискретных устройств и релейно-контактных схем. Упрощение и преобразование схем. |
1. Минимизация логических функций
Методы минимизации булевых функций:
Метод Квайна.
Метод Квайна - МакКласски.
Метод Блейка - Порецкого.
Метод диаграмм Вейча.
Метод минимизирующих карт.
Метод Петрика.
Минимизация частично определенных булевых функций.
Минимизация систем булевых функций.
Одним из методов построения минимальной ДНФ логической функции является метод Квайна - МакКласски.Формализация производится следующим образом:
1. Все наборы единицы из СДНФ булевой функции f записываются их двоичными номерами.
2. Все номера разбиваются на непересекающиеся группы. Признак образования i -й группы: i единиц в каждом двоичном номере наборы единицы.
|
|
|
3. Склеивание производят только между номерами соседних групп. Склеиваемые номера отмечаются каким-либо знаком (зачеркиванием).
4. Производят всевозможные склеивания. Неотмеченные после склеивания номера являются простыми импликантами.
Нахождение минимальных ДНФ далее производится по импликантной матрице.
Примеры выполнения заданий
1. Минимизируйте методом Квайна - МакКласски булеву функцию
f(x1, x2,x3, x4), заданную таблицей истинности:
В СДНФ функции f(x1, x2,x3, x4), заменим все наборы единицы их
| двоичными номерами: f = 0001 Ú 0011 Ú 0101 Ú 0111 Ú 1110 Ú 1111. | x4x3x2x1 | f |
| Образуем группы двоичных номеров. Признаком образования i - й группы является i единиц в двоичном номере наборы единицы. | 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 | 0 1 0 1 0 1 0 1 0 0 0 0 0 0 1 1 |
| Номер группы | Двоичные номера наборов единицы | |
| - | ||
| 0011, 0101 | ||
| 0111, 1110 | ||
Склеим номера из соседних групп таблицы. Склеиваемые номера вычеркнем (прим. - выделено цветом). Результаты склеивания занесем в следующую таблицу.
| Склеим номера из соседних групп. Склеиваться могут только номера, имеющие звездочки в одинаковых позициях. Склеиваемые номера вычеркнем. Результаты склеивания занесем в таблицу: |
|
Имеем три простые импликанты: *111, 111*, 0**1. Строим импликантную матрицу. По таблице определяем совокупность простых импликант - 0**I и 111*, соответствующую минимальной ДНФ. Для восстановления буквенного вида простой импликанты достаточно выписать произведения тех переменных, которые соответствуют сохранившимся двоичным цифрам.
| Простые импликанты | Наборы единицы | |||||
| 0**1 | X | X | X | X | ||
| *111 | X | X | ||||
| 111* | X | X |
0**1 —> 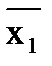 x4; 111* —> x1x2x3. Итак, МДНФ =
x4; 111* —> x1x2x3. Итак, МДНФ = 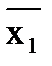 x4 Ú x1x2x3
x4 Ú x1x2x3
2. Применение булевых функций для анализа и синтеза дискретных устройств. Упрощение и преобразование комбинационных схем
Преобразование информации в блоках ПК производится логическими устройствами двух типов: комбинационными схемами и цифровыми автоматами с памятью.
|
|
|
Логический элемент И (конъюнктор) реализует операцию логического умножения (см. рис. 1). Логический элемент ИЛИ (дизъюнктор) реализует операцию логического сложения (см. рис. 2). Логический элемент НЕ (инвертор) реализует операцию отрицания
(см. рис. 3). Логический элемент И-НЕ реализует функцию штрих Шеффера (см. рис. 4). Логический элемент ИЛИ-НЕ реализует функцию стрелка Пирса (см. рис. 5).
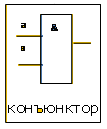 Рис.1
Рис.1
|  Рис.2
Рис.2
|  Рис.3
Рис.3
|
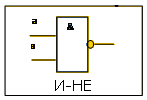 Рис.4
Рис.4
| 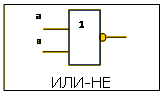 Рис.5
Рис.5
|
Примеры выполнения заданий
1. Укажите функцию F(a, b, c, d), реализуемую схемой из функциональных элементов предварительно упростив:
a b c d
| & |
| & |
Решение: F(a, b, c, d) = a & c Ú 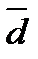 Ú с & b º c &(a Ú b) Ú
Ú с & b º c &(a Ú b) Ú 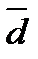 .
.
|
|
|
|
|
Дата добавления: 2014-11-20; Просмотров: 969; Нарушение авторских прав?; Мы поможем в написании вашей работы!