Перечисление графов

Свойства деревьев

Деревья

Определение. Связный граф, не содержащий циклов, называется деревом (рисунок 6.65).

Рисунок 6.65 – Дерево

Несвязный граф, не содержащий циклов, называется лесом.

Пример. На рисунке 6.66 приведен трехкомпонентный лес. Первую компоненту образует дерево с вершинами 1,2,3,4, вторую – 5,6,7,8,9, третью – 10,11.

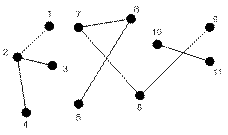
Рисунок 6.66 – Лес

Теорема 6.9. Всякое дерево содержит 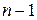ребер, где 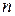– число вершин.

Теорема 6.10. Всякий лес содержит ребер, где 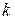– число компонент связности.

Теорема 6.11. Любые две вершины дерева соединены точно одной простой цепью.

Теорема 6.12. Если в дереве любые две вершины соединить ребром, то в графе появится один цикл.

Определение. Граф 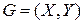называется помеченным, если его вершинам присвоены фиксированные метки, например, номера .

Два помеченных графа одинаковы (не различаются), если их вершины помечены одной системой меток и существует изоморфизм одного графа на другой, при котором сохраняются метки всех вершин.

Пример. На рисунке 6.67 изображены все помеченные графы с числом вершин ; их количество равно 8.

Рисунок 6.67

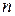Количество (неориентированных) помеченных графов (простых с вершинами и 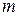ребрами) равно числу сочетаний из множества различных неориентированных пар вершин 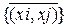по числу ребер .

,

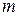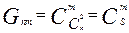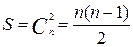
Суммируя числа по всем возможным количествам ребер от случая безреберного графа до случая полного графа с 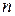вершинами, получаем число всех помеченных графов с 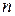вершинами:

Число 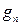неизоморфных графов без пометок (простых, неориентированных) найти значительно труднее. Среди восьми графов на рисунке 3 без учета пометок можно указать только четыре попарно неизоморфных друг другу, например, в квадратах 1, 2, 7, 8. Следовательно, , что вдвое меньше числа 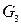помеченных графов. Число помеченных четырехвершинных графов равно 64, в то время как различных неизоморфных четырехвершинных графов без пометок существует всего .

Если через 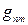обозначить число неизоморфных 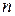-вершинных графов с 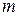ребрами, то:

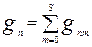
В общем случае количество неизоморфных графов 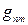, 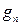находятся с помощью теории перечисления конфигураций, созданной Д. Пойа.

Дата добавления: 2014-11-20