
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства определителей. 3 страница
|
|
|
|
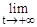
 =e.
Итак
=e.
Итак 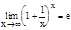 Замечание.
Следует отметить, что
Замечание.
Следует отметить, что  (1+a(х))1/a(х)=е;
(1+a(х))1/a(х)=е;
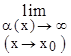 (1+1/a(х))a(х)=е
Не забудьте!!! В формуле 2 огозамечательного предела всегда «добавка» к единице является бесконечно малой, а показатель степени является обратной величиной этой бесконечно малой.
Определение непрерывности функции в точке.
Предположим, что нам задана функция f(x), определенная в некоторой области X={x}, причем полагаем, что предельная точка х=х0 является внутренней точкой множества Х.
Замечание. При определении предела функции было не обязательно, чтобы предельная точка х=х0 принадлежала множеству области определения f(x).
Определение. Функция f(x) называется непрерывной в точке х=х0, если она имеет этой в точке предел равный значению f(x0), т.е.
(1+1/a(х))a(х)=е
Не забудьте!!! В формуле 2 огозамечательного предела всегда «добавка» к единице является бесконечно малой, а показатель степени является обратной величиной этой бесконечно малой.
Определение непрерывности функции в точке.
Предположим, что нам задана функция f(x), определенная в некоторой области X={x}, причем полагаем, что предельная точка х=х0 является внутренней точкой множества Х.
Замечание. При определении предела функции было не обязательно, чтобы предельная точка х=х0 принадлежала множеству области определения f(x).
Определение. Функция f(x) называется непрерывной в точке х=х0, если она имеет этой в точке предел равный значению f(x0), т.е. 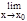 f(x)=f(x0).
Определение по Коши. Функция f(x) непрерывна в точке х=х0,
если по " e>0, $ d(e)>0 такое, что при всех х из |x-x0|< d => |f(x)-f(x0)|< e.
Определение по Гейне. Функция f(x) непрерывна в точке х=х0, если для любой сходящейся к х0 последовательности xn®x0, имеем f(xn)®f(x0).
Важно отметить, что равенство
f(x)=f(x0).
Определение по Коши. Функция f(x) непрерывна в точке х=х0,
если по " e>0, $ d(e)>0 такое, что при всех х из |x-x0|< d => |f(x)-f(x0)|< e.
Определение по Гейне. Функция f(x) непрерывна в точке х=х0, если для любой сходящейся к х0 последовательности xn®x0, имеем f(xn)®f(x0).
Важно отметить, что равенство  f(x)=f(x0) можно записать в виде
f(x)=f(x0) можно записать в виде 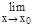 f(x)=f(
f(x)=f(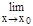 x).
То есть для непрерывных функций возможно переставить местами символы «функция» и «предел», что очень важно при вычислении пределов.
Определению непрерывности функции f(x) в точке х=х0 можно придать другую форму: дадим аргументу х в точке х=х0, приращение Dх=х-х0, тогда разность f(x)-f(x0)=Dy представляет собой приращение функции в точке х=х0, соответствующее приращению аргумента Dх, т.е. DуºDf(x0)=f(x0+Dx)-f(x0).
Из определения непрерывности f(x) следует, что при Dх®0 (х®х0) имеет место Dу®0 (f(x)®f(x0)), т.е.
x).
То есть для непрерывных функций возможно переставить местами символы «функция» и «предел», что очень важно при вычислении пределов.
Определению непрерывности функции f(x) в точке х=х0 можно придать другую форму: дадим аргументу х в точке х=х0, приращение Dх=х-х0, тогда разность f(x)-f(x0)=Dy представляет собой приращение функции в точке х=х0, соответствующее приращению аргумента Dх, т.е. DуºDf(x0)=f(x0+Dx)-f(x0).
Из определения непрерывности f(x) следует, что при Dх®0 (х®х0) имеет место Dу®0 (f(x)®f(x0)), т.е.  Dу=0.
(
Dу=0.
(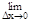 (f(x0+Dх)-f(x0))=0).
Итак, непрерывная в точке функция характеризуется тем, что бесконечно малому приращению аргумента Dх соответствует бесконечно малое приращение функции Dу.
(f(x0+Dх)-f(x0))=0).
Итак, непрерывная в точке функция характеризуется тем, что бесконечно малому приращению аргумента Dх соответствует бесконечно малое приращение функции Dу.
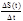 .
Если мы хотим найти скорость точки в данный момент (мгновенную скорость), а именно в момент времени t, нужно вычислить предел
.
Если мы хотим найти скорость точки в данный момент (мгновенную скорость), а именно в момент времени t, нужно вычислить предел  Vср=
Vср= 
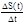 .
Таким образом находим скорость изменения функции S(t) в момент времени t.
б. Линейная плотность стержня.
Если стержень является неоднородным, то очевидной характеристикой стержня является плотность его в данной точке, которая определяется как отношение массы стержня к его длине. Находим среднюю плотность стержня на промежутке [x, x+Dx]
rcр=
.
Таким образом находим скорость изменения функции S(t) в момент времени t.
б. Линейная плотность стержня.
Если стержень является неоднородным, то очевидной характеристикой стержня является плотность его в данной точке, которая определяется как отношение массы стержня к его длине. Находим среднюю плотность стержня на промежутке [x, x+Dx]
rcр= 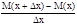 =
= 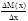 Тогда плотность стержня в точке х выразится пределом
r(х)=
Тогда плотность стержня в точке х выразится пределом
r(х)=  rcр=
rcр= 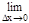
 .
в. Задача о касательной к кривой.
Пусть уравнение y=f(x) задает в плоскости Оху, некоторую кривую l. Для данной кривой ставится задача: определить наклон касательной к этой кривой, проведенной в точке (x, f(x)), т.е. определить тангенс угла между касательной и положительным направлением оси Ох. При этом касательной к кривой l в точке (x, f(x)) называется предельное положение секущей, проходящей через точки (x, f(x)) и (x+Dx, f(x+Dx))
при Dх®0.
Находим тангенс угла наклона секущей L:
tg a=
.
в. Задача о касательной к кривой.
Пусть уравнение y=f(x) задает в плоскости Оху, некоторую кривую l. Для данной кривой ставится задача: определить наклон касательной к этой кривой, проведенной в точке (x, f(x)), т.е. определить тангенс угла между касательной и положительным направлением оси Ох. При этом касательной к кривой l в точке (x, f(x)) называется предельное положение секущей, проходящей через точки (x, f(x)) и (x+Dx, f(x+Dx))
при Dх®0.
Находим тангенс угла наклона секущей L:
tg a= 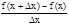 =
= 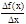
 tg b=
tg b= 
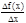 , где b - угол наклона касательной к кривой в точке (x, f(x)), который она составляет с положительным направлением оси Ох. Из приведенных примеров следует, что многие практические задачи физики, геометрии и техники сводятся к вычислению предела частного, в числителе которого стоит приращение функции, а в знаменателе приращение аргумента, вызвавшее это приращение.
Производная функции в точке.
Определение. Производной функции y=f(x) в точке называется предел отношения приращения функции (Dу) в этой точке к соответствующему приращению аргумента (Dх) при стремлении последнего к нулю, то есть
y'(x)=
, где b - угол наклона касательной к кривой в точке (x, f(x)), который она составляет с положительным направлением оси Ох. Из приведенных примеров следует, что многие практические задачи физики, геометрии и техники сводятся к вычислению предела частного, в числителе которого стоит приращение функции, а в знаменателе приращение аргумента, вызвавшее это приращение.
Производная функции в точке.
Определение. Производной функции y=f(x) в точке называется предел отношения приращения функции (Dу) в этой точке к соответствующему приращению аргумента (Dх) при стремлении последнего к нулю, то есть
y'(x)= 
 при условии, что этот предел существует. Принято обозначать производную функции у=f(x) в точке х как y'(x) или
при условии, что этот предел существует. Принято обозначать производную функции у=f(x) в точке х как y'(x) или 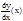 .
Дифференциа́л — линейная часть приращения функции.
Дифференцируемость функции.
Определение. Функция y=f(x) называется дифференцируемой в точке х, если приращение Dу функции f(x) в точке х, отвечающее приращению аргумента Dх, может быть представлено в виде Dу=А×Dх+a(Dх)×Dх, где А - постоянное число (для точки х), не зависящее от Dх; a(Dх) - бесконечно малая функция Dх, т.е.
.
Дифференциа́л — линейная часть приращения функции.
Дифференцируемость функции.
Определение. Функция y=f(x) называется дифференцируемой в точке х, если приращение Dу функции f(x) в точке х, отвечающее приращению аргумента Dх, может быть представлено в виде Dу=А×Dх+a(Dх)×Dх, где А - постоянное число (для точки х), не зависящее от Dх; a(Dх) - бесконечно малая функция Dх, т.е.  a(Dх)=0.
Иначе говоря, приращение Dу имеет вид Dу=А×Dх+о(Dх).
Далее покажем дифференцируемость некоторых функций.
1. у=х2+2. Dу=(х+Dх)2+2-х2-2=2хDх+Dх2. А=2х; a(Dх)=Dх.
2. у=ln x. Dy=ln(x+Dx)-ln x=ln(1+Dx/x)=Dx/x+о(Dx)
3. у=sin x. Dy=sin(x+Dx)-sin x=2sin(Dx/2)cos(Dx/2+x)=
=2(Dx/2+о(Dx))[cos x+(cos(x+Dx/2)-cos x)]=
=[Dx+2×о(Dx)]cos x-[Dx+2o(Dx)]sin(x+Dx/4)sinDx/2=
=[Dx+2×о(Dx)]cos x-[Dx+2×о(Dx)][Dx/2+о(Dx)]sin(x+Dx/4)=
=cos x Dx+2cos x×о(Dx)-(Dx)2×(f(Dx, x))=cos x Dx+о(Dx).
Теорема. Для того чтобы функция f(x) была дифференцируемой в точке х, необходимо и достаточно чтобы f(x) имела в этой точке производную.
Доказательство.
1. Необходимость. Пусть y=f(x) в т. х дифференцируема, тогда Dу=А×Dх+о(Dх). Разделим Dу на Dх и вычислим предел частного
a(Dх)=0.
Иначе говоря, приращение Dу имеет вид Dу=А×Dх+о(Dх).
Далее покажем дифференцируемость некоторых функций.
1. у=х2+2. Dу=(х+Dх)2+2-х2-2=2хDх+Dх2. А=2х; a(Dх)=Dх.
2. у=ln x. Dy=ln(x+Dx)-ln x=ln(1+Dx/x)=Dx/x+о(Dx)
3. у=sin x. Dy=sin(x+Dx)-sin x=2sin(Dx/2)cos(Dx/2+x)=
=2(Dx/2+о(Dx))[cos x+(cos(x+Dx/2)-cos x)]=
=[Dx+2×о(Dx)]cos x-[Dx+2o(Dx)]sin(x+Dx/4)sinDx/2=
=[Dx+2×о(Dx)]cos x-[Dx+2×о(Dx)][Dx/2+о(Dx)]sin(x+Dx/4)=
=cos x Dx+2cos x×о(Dx)-(Dx)2×(f(Dx, x))=cos x Dx+о(Dx).
Теорема. Для того чтобы функция f(x) была дифференцируемой в точке х, необходимо и достаточно чтобы f(x) имела в этой точке производную.
Доказательство.
1. Необходимость. Пусть y=f(x) в т. х дифференцируема, тогда Dу=А×Dх+о(Dх). Разделим Dу на Dх и вычислим предел частного  при Dх®0:
при Dх®0:

 =
=  (А+
(А+  )=А.
С другой стороны
)=А.
С другой стороны 
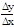 =f '(x). Значит f '(x) существует и равна А.
2. Достаточность. Пусть функция y=f(x) имеет производную, т.е.
=f '(x). Значит f '(x) существует и равна А.
2. Достаточность. Пусть функция y=f(x) имеет производную, т.е. 
 =у'(x), тогда разность функции
=у'(x), тогда разность функции  и предела y'(x) есть величина бесконечно малая при Dх®0, т.е.
и предела y'(x) есть величина бесконечно малая при Dх®0, т.е.  -y'(x)=a(Dх); a(Dх)®0 приDх®0, Dу=y'(x)×Dx+a(Dx)×Dx. Пусть y'(x)=A для точки х, тогда Dу=А×Dх+a(Dх)×Dх.
Теорема доказана.
Теорема. Дифференцируемая в точке х функция y=f(x) непрерывна в этой точке.
Доказательство. Так как Dу=А×Dх+о(Dх) - условие дифференцируемости, то при Dх®0 получаем Dу®0. Последнее означает непрерывность функции f(x) в точке х.
Замечание. Дифференцируемая в точке х=х0 функция у=f(x) имеет в точке (х0; f(x0)) касательную прямую.
-y'(x)=a(Dх); a(Dх)®0 приDх®0, Dу=y'(x)×Dx+a(Dx)×Dx. Пусть y'(x)=A для точки х, тогда Dу=А×Dх+a(Dх)×Dх.
Теорема доказана.
Теорема. Дифференцируемая в точке х функция y=f(x) непрерывна в этой точке.
Доказательство. Так как Dу=А×Dх+о(Dх) - условие дифференцируемости, то при Dх®0 получаем Dу®0. Последнее означает непрерывность функции f(x) в точке х.
Замечание. Дифференцируемая в точке х=х0 функция у=f(x) имеет в точке (х0; f(x0)) касательную прямую.
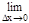
 =
=  (fj'×jx'+fj' a(Dx)+a(Dj)×
(fj'×jx'+fj' a(Dx)+a(Dj)×  )=fj'×jx'.
Окончательно имеем fx'(j(x))=fj'×jx'.
Производная неявной функции.
Пусть значения двух переменных х и у связаны между собой уравнением вида F(x, y)=0.
Пример: у+
)=fj'×jx'.
Окончательно имеем fx'(j(x))=fj'×jx'.
Производная неявной функции.
Пусть значения двух переменных х и у связаны между собой уравнением вида F(x, y)=0.
Пример: у+ 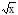 =0, x2+ln y=0.
Определение. Если функция y=f(x), определенная на некотором интервале (a, b) такова, что уравнение F(x, y)=0 при подстановке в него y=f(x) обращается в тождество относительно х, то функция у=f(x) называется неявно заданной уравнением F(x, y)=0.
Частные производные функции z=F(x, y).
Определение. Если существует предел
=0, x2+ln y=0.
Определение. Если функция y=f(x), определенная на некотором интервале (a, b) такова, что уравнение F(x, y)=0 при подстановке в него y=f(x) обращается в тождество относительно х, то функция у=f(x) называется неявно заданной уравнением F(x, y)=0.
Частные производные функции z=F(x, y).
Определение. Если существует предел 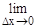
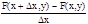 , то он называется частной производной по переменному х функции z=F(x, y) в точке (х, у) и обозначается символами zx' или Fx'(x, y).
Определение. Если существует предел
, то он называется частной производной по переменному х функции z=F(x, y) в точке (х, у) и обозначается символами zx' или Fx'(x, y).
Определение. Если существует предел 
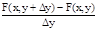 , то он называется частной производной по переменному у функции z=F(x, y) в точке (х, у) и обозначается символами zy' или Fy'(x, y).
Полное приращение F(x, y)
Пусть имеем функцию двух переменных z=F(x, y), где у=f(x) дифференцируемая функция; т.е. F(x, y) является функцией переменного х как сложная функция z=F(x, f(x)). Если переменная х получает приращение Dх, то переменная у=f(x) также принимает приращение Dу в силу непрерывности f(x). Откуда получим:
DF(x)=F(x+Dx, y+Dy)-F(x, y)=F(x+Dx, y+Dy)-F(x, y+Dy)+F(x, y+Dy)-F(x, y)= =DxF(x, y+Dy)+DyF(x, y). тогда после деления равенства на Dх и перехода к пределу при Dх®0 получим:
, то он называется частной производной по переменному у функции z=F(x, y) в точке (х, у) и обозначается символами zy' или Fy'(x, y).
Полное приращение F(x, y)
Пусть имеем функцию двух переменных z=F(x, y), где у=f(x) дифференцируемая функция; т.е. F(x, y) является функцией переменного х как сложная функция z=F(x, f(x)). Если переменная х получает приращение Dх, то переменная у=f(x) также принимает приращение Dу в силу непрерывности f(x). Откуда получим:
DF(x)=F(x+Dx, y+Dy)-F(x, y)=F(x+Dx, y+Dy)-F(x, y+Dy)+F(x, y+Dy)-F(x, y)= =DxF(x, y+Dy)+DyF(x, y). тогда после деления равенства на Dх и перехода к пределу при Dх®0 получим:

 =
= 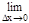
 +
+ 
 =
= 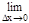
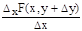 +
+ 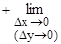
 ×
×  =Fx'(x, y)+Fy'(x, y)×y'(x)
Итак: для того чтобы вычислить производную функции у=f(x), заданной неявно уравнением F(x, y)=0, нужно приравнять нулю производную левой части как производную сложной функции, считая у функцией х, т.е. у=f(x). При этом получим равенство Fx'+Fy'×yx'=0 или yx'=
=Fx'(x, y)+Fy'(x, y)×y'(x)
Итак: для того чтобы вычислить производную функции у=f(x), заданной неявно уравнением F(x, y)=0, нужно приравнять нулю производную левой части как производную сложной функции, считая у функцией х, т.е. у=f(x). При этом получим равенство Fx'+Fy'×yx'=0 или yx'= 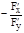 . Fy'¹0.
Здесь Fx' и Fy' - частные производные F(x, y) по переменным х и у соответственно.
Например.
1. х2+у2-а2=0. 2х+2y×y'=0, yx'=-x/y; y¹0.
2. sin x+yx=0. cos x+y+y'×x=0, yx'=
. Fy'¹0.
Здесь Fx' и Fy' - частные производные F(x, y) по переменным х и у соответственно.
Например.
1. х2+у2-а2=0. 2х+2y×y'=0, yx'=-x/y; y¹0.
2. sin x+yx=0. cos x+y+y'×x=0, yx'=  (-y-cos x)=
(-y-cos x)=  (-cos x+
(-cos x+  ). x¹0.
). x¹0.
 .
Доказательство. Дадим приращение Dу переменной у в точке у*, тогда обратная функция х=j(у) получит соответствующее приращение Dх=Dj(у*). Заметим, что приращения Dх и Dу отличны от нуля, так как функции j(у) и f(x) строго монотонны. Далее составим частное
.
Доказательство. Дадим приращение Dу переменной у в точке у*, тогда обратная функция х=j(у) получит соответствующее приращение Dх=Dj(у*). Заметим, что приращения Dх и Dу отличны от нуля, так как функции j(у) и f(x) строго монотонны. Далее составим частное 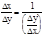 . При переходе к пределу при Dу®0 (очевидно Dх®0), получим xy¢(y*)=
. При переходе к пределу при Dу®0 (очевидно Dх®0), получим xy¢(y*)= 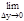
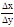 =
=  =
= 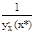 . Следовательно j¢(y)|y=y*=
. Следовательно j¢(y)|y=y*=  .
Вывод призводных
1. y=logax, y'=
.
Вывод призводных
1. y=logax, y'=  .
Так как Dy=loga(x+Dx)-logax=loga(1+Dx/x), вычислим
.
Так как Dy=loga(x+Dx)-logax=loga(1+Dx/x), вычислим

 =
= 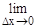
 ×loga(1+Dx/x)=
×loga(1+Dx/x)= 
 =
= 

 ==
==  ×
× 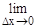
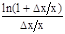 =
= 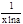 .
2. y=ctg x, y'=
.
2. y=ctg x, y'=  .
Dy=ctg(x+Dx)-ctg x=
.
Dy=ctg(x+Dx)-ctg x= 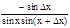 ;
y'=
;
y'= 
 =
= 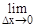
 =
= 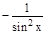 .
3. (arcsin x)'=
.
3. (arcsin x)'=  Доказательство. Если у=arcsin x, то обратная функция x=sin y. Причем уÎ(-p/2; p/2), а тогда cos y>0. В силу предыдущей теоремы имеем.
Доказательство. Если у=arcsin x, то обратная функция x=sin y. Причем уÎ(-p/2; p/2), а тогда cos y>0. В силу предыдущей теоремы имеем.
 .;
4. (arccos x)'=-
.;
4. (arccos x)'=-  Доказательство. у=arccos x; x=cosy, yÎ(0, p), sin y>0. Тогда
Доказательство. у=arccos x; x=cosy, yÎ(0, p), sin y>0. Тогда
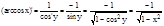 .;
5. (arctg x)'=
.;
5. (arctg x)'=  Доказательство. y=arctg x; x=tg y. Поэтому имеем
Доказательство. y=arctg x; x=tg y. Поэтому имеем
 .;
6. (arcctg x)'= -
.;
6. (arcctg x)'= - 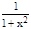 Доказательство. y=arcсtg x; x=сtg y. Поэтому имеем
Доказательство. y=arcсtg x; x=сtg y. Поэтому имеем
 .;
.;