Связь линейных отображений с матрицами. 2 страница

11. Найти двойственное отображение L* к линейному отображению:

L

12. Найти двойственное отображение к линейному отображению из задачи №8, и вычислить его ранг.

13. Найти двойственное отображение к линейному отображению L и вычислить его ранг.

§ 6. Евклидовы пространства.

Определение 19. Линейное пространство V называется евклидовым, если для любых его двух элементов х и у определено число, обозначаемое (х,у), и это соответствие удовлетворяет следующим соотношениям:

1.

2. Для любых чисел α, β и любых элементов x, y, z из V

3. , причем

Число, о котором говорится в определении, называется скалярным произведением элементов х и у.

Из этих свойств сразу же вытекает теорема.

Теорема 8 (Неравенство Коши-Буняковского). Для любых элементов х, у из V имеет место неравенство:

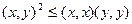, причем неравенство достигается, только если существует такое число α, что .

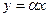Доказательство. Для любых х, у из V и произвольного t, рассмотрим квадратный трехчлен:

.

Согласно свойству 3, этот квадратный трехчлен принимает значения ≥0, причем равенство 0будет возникать только в случае . Но, как следует из элементарной алгебры, такое возможно, только если:

А) дискриминант квадратного трехчлена <0 (в случае, когда трехчлен принимает только положительные значения).

Б) дискриминант квадратного трехчлена равен 0 в случае, когда квадратный трехчлен принимает положительные значения и 0.

Это означает, что в случае (а) , а в случае (б) 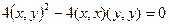, причем только если для некоторого 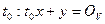. Что и доказывает теорему.

Определение 20. Два элемента х, у из V называются ортогональными, если .

Определение 21. Базис 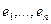пространства V называется ортонормированным, если e_i и e_j для всех пар ортогональны и для всех .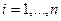

Теорема 9 (теорема Грамма-Шмидта). В пространстве существует ортонормированный базис.

Доказательство. Доказательство проведем методом ортогонализации Штурма. Пусть дан произвольный базис пространства V.

1. Полагаем . Легко видеть, что пространства V и .

2. Предположим, что уже построены. Причем образуют базис пространства V и для любых . Тогда полагаем .

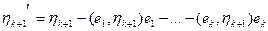Имеем: а) 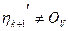, так как иначе , что противоречит тому, что - базис.

б) для всех 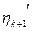ортогонально .

Действительно,

.

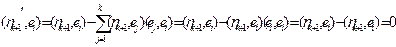Полагая 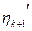получим: 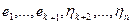базис. Действительно, если , и так как - базис, то 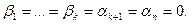Но тогда 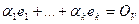, и так как линейно независимы, то 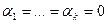. Далее 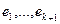попарно ортогональны и для любого i .

3. Повторяем процедуру, описанную в пункте (2) до тех пор, пока k не станет равным n. Тогда элементы будут образовывать ортонормированный базис. Теорема доказана.

Поставим теперь вопрос: как задавать скалярное произведение в пространстве V? Для этого рассмотрим базис пространства V. Легко видеть, что для элементов 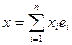и имеем:

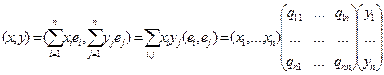, где .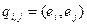

Легко видеть, что матрица полностью описывает скалярное произведение в пространстве V с фиксированным базисом . Мы будем ее называть матрицей скалярного произведения. Отметим, что Q – симметричная матрица.

Посмотрим, как сказывается на матрице Q изменение базиса. Пусть - другой базис пространства V и пусть

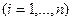
- матрица перехода.

Тогда:

,

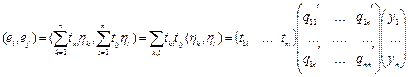Где 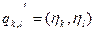. Отсюда следует формула, связывающая матрицы скалярного произведения в различных базисах: .

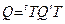Можно показать (мы это сделаем в дополнении к § 6), что всегда можно подобрать такую матрицу Т, что 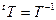(то есть Q и Q’ подобны), а Q’ – диагональная матрица. Если на матрицу Т не накладывать никаких условий, то, взяв в качестве Т матрицу перехода к ортонормированному базису, мы получим: .

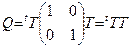В частности отсюда следует, что любая матрица скалярного произведения может быть представлена в виде произведения некоторой матрицы на транспонированную.

Условие (3) в определении скалярного произведения накладывает на матрицу Q следующее условие: для любых чисел 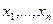не всех равных 0, произведение:

.

Симметричные матрицы, удовлетворяющие этому условию, называются положительно определенными. Существует следующий критерий Сильвестра положительной определенности: если 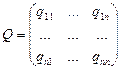, то Q положительно определена тогда и только тогда, когда выполняются неравенства:

Дополнение к § 6 (Приведение к диагональному виду ортогональными преобразованиями)

Покажем, что у симметричной матрицы все собственные числа вещественны. Итак, пусть:

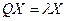, где λ и Х – комплексные. Тогда, переходя к сопряженным, получим: 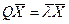, или .

Вычислим 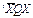, где

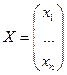
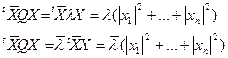
Отсюда:

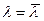, и, следовательно, , то есть λ вещественно. Далее мы воспользуемся тем фактом, что у Q число собственных векторов равно п (см. 4). Легко показать, что если Х и У принадлежат разным собственным числам λ и μ, то они ортогональны:

Если Х и У принадлежат одному собственному числу λ, то, используя метод ортогонализации Штурма, их можно заменить на ортогональные собственные вектора, принадлежащие числу λ. Таким образом, у матрицы Q можно найти п ортогональных собственных векторов 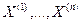. Умножая на скалярный множитель, можно добиться, что 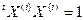. Тогда положим 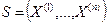. Имеем:

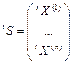
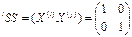
Тогда:

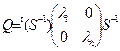
И, взяв за матрицу перехода , построим базис, в котором матрица скалярного произведения становится диагональю.

§ 7. Квадратичные формы.

Определение 22. Пусть дана симметричная матрица Q и вектор 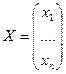, координаты которого являются переменными. Тогда многочлен:

Называется квадратичной формой. А матрица Q называется матрицей квадратичной формы.

Легко видеть, что по квадратичной форме можно восстановить матрицу Q. Действительно, пусть:

Тогда полагаем: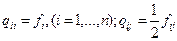

.

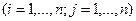
Получается взаимнооднозначное соответствие между матрицами и квадратичными формами. Если в квадратичной форме провести замену переменных (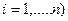, то получим:

Пусть , тогда:

.

Таким образом, переход к другим переменным соответствует переходу к другому базису, причем 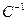- матрица перехода (см. § 6). Поэтому последние результаты § 6 можно истолковать как приведение квадратичной формы к диагональному виду ортогональными преобразованиями, то есть соответствующими движению в пространстве. Геометрически это означает, что, взяв уравнение поверхности второго порядка 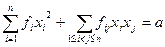, мы передвигаем систему координат так, чтобы уравнение поверхности приняло простейший (канонический) вид: .

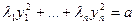Пример.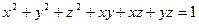

; найдем собственные числа матрицы Q.

А) 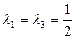Найдем собственные вектора, соответствующие собственному числу .

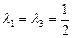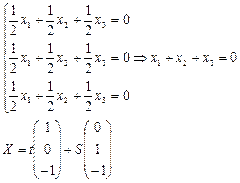
Построим пару ортогональных собственных векторов.

;

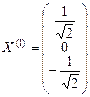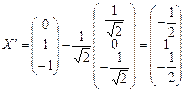
Б) Теперь ищем собственные векторы для

,

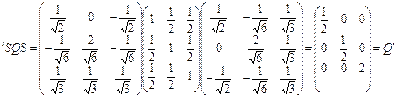
Следовательно, сделав замену:

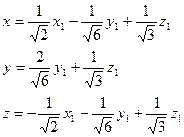
Получим уравнение:

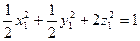
Таким образом, исходная поверхность второго порядка представляет собой эллипсоид вращения, с полуосями , и .

Задачи к § 6 и § 7.

1. Найти скалярное произведение векторов , 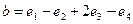в базисе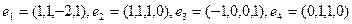

2. Найти скалярное произведение векторов , 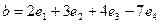в базисе

3. Пусть скалярное произведение задается формой:

. Найти скалярное произведение векторов 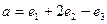и

4. Пусть скалярное произведение задается формой:

. Найти скалярное произведение векторов:

,

5. Построить оригинальный базис в пространстве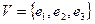

6. Построить оригинальный базис в пространстве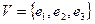

7. Построить ортогональный базис в пространстве

8. Привести квадратичную форму к диагональному виду при помощи ортогональных преобразований.

9. Привести квадратичную форму к диагональному виду при помощи ортогональных преобразований.

Литература.

1. Боревич З. И. Определители и матрицы. Наука, 1973

2. Мальцев А. И. Основы линейной алгебры. Наука, 1975

3. Гантмахер Ф. Р. Теория матриц. Наука, 1988

4. Ван-дер-Варден Б. Л. Алгебра. Наука, 1976

5. Фаддеев Д. К., Соминский И. О. Сборник задач по линейной алгебре.

6. Проскуряков. Задачи по линейной алгебре.

Содержание.

Введение. 2

§ 1. Линейные пространства. 3

§ 2. Линейные подпространства. 6

§ 3. Линейные отображения. 10

§ 4. Композиция линейных отображений. 12

§ 5. Двойственное пространство и двойственное отображение. 14

§ 6. Евклидовы пространства. 19

§ 7. Квадратичные формы. 23

Литература. 27

Дата добавления: 2014-12-08