
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Где -объём параллелепипеда, построенного на векторах , и . 2 страница
|
|
|
|
 .
.
Пересечением множеств 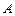 и
и  называется множество
называется множество
 .
.
Разностью множеств 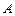 и
и  называется множество
называется множество
 .
.
Дополнением множества 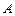 (до универсального множества
(до универсального множества 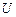 ) называется множество
) называется множество  .
.
Два множества 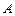 и
и  называются эквивалентными и пишут
называются эквивалентными и пишут 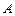 ~
~  , если между элементами этих множеств может быть установлено взаимно однозначное соответствие. Множество
, если между элементами этих множеств может быть установлено взаимно однозначное соответствие. Множество 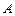 называется счётным, если оно эквивалентно множеству натуральных чисел
называется счётным, если оно эквивалентно множеству натуральных чисел  :
: 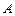 ~
~  . Пустое множество по определению относится к счётным.
. Пустое множество по определению относится к счётным.
Понятие мощности множества возникает при сравнении множеств по числу содержащихся в них элементов. Мощность множества 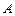 обозначают
обозначают  . Мощностью конечного множества является число его элементов.
. Мощностью конечного множества является число его элементов.
Эквивалентные множества обладают равной мощностью. Множество 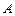 называется несчётным, если его мощность больше мощности множества
называется несчётным, если его мощность больше мощности множества  .
.
Действительным (вещественным) числом называется бесконечная десятичная дробь, взятая со знаком «+» или « ». Действительные числа отождествляют с точками числовой прямой. Модулем (абсолютной величиной) действительного числа
». Действительные числа отождествляют с точками числовой прямой. Модулем (абсолютной величиной) действительного числа  называется неотрицательное число:
называется неотрицательное число:
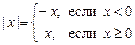
Множество 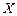 называется числовым, если его элементами
называется числовым, если его элементами  являются действительные числа.Числовыми промежутками называются множества чисел:
являются действительные числа.Числовыми промежутками называются множества чисел: 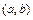 ,
, 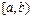 ,
, 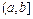 ,
,  ,
, 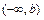 ,
, 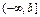 ,
,  ,
,  ,
, 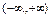 .
.
Множество всех точек  на числовой прямой, удовлетворяющих условию
на числовой прямой, удовлетворяющих условию  , где
, где 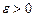 - сколь угодно малое число, называется
- сколь угодно малое число, называется  - окрестностью (или просто окрестностью) точки
- окрестностью (или просто окрестностью) точки 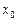 и обозначается
и обозначается 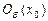 . Множество всех точек
. Множество всех точек  условием
условием  , где
, где 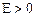 - сколь угодно большое число, называется
- сколь угодно большое число, называется  - окрестностью (или просто окрестностью) бесконечности и обозначается
- окрестностью (или просто окрестностью) бесконечности и обозначается 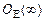 .
.
Величина, сохраняющая одно и тоже числовое значение, называется постоянной. Величина, принимающая различные числовые значения, называется переменной. Функцией 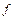 называется правило, по которому каждому числу
называется правило, по которому каждому числу 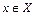 ставится в соответствие одно вполне определённое число
ставится в соответствие одно вполне определённое число  , и пишут
, и пишут 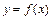 . Множество
. Множество  называется областью определения функции,
называется областью определения функции,  - множеством ( или областью ) значений функции,
- множеством ( или областью ) значений функции, 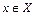 - аргументом,
- аргументом, 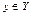 - значением функции. Наиболее распространённым способом задания функции является аналитический способ, при котором функция задаётся формулой. Естественной областью определения функции
- значением функции. Наиболее распространённым способом задания функции является аналитический способ, при котором функция задаётся формулой. Естественной областью определения функции 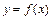 называется множество
называется множество  значений аргумента
значений аргумента 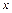 , для которого данная формула имеет смысл. Графиком функции
, для которого данная формула имеет смысл. Графиком функции 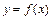 ,
, 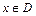 в прямоугольной системе координат
в прямоугольной системе координат 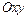 , называется множество всех точек плоскости с координатами
, называется множество всех точек плоскости с координатами 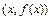 ,
, 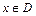 .
.
|
|
|
Функция 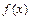 называется чётной на множестве
называется чётной на множестве  , симметричном относительно точки
, симметричном относительно точки 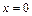 , если для всех
, если для всех 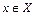 выполняется условие:
выполняется условие: 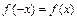 и нечётной, если выполняется условие
и нечётной, если выполняется условие 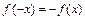 . В противном случае
. В противном случае 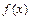 - функция общего вида или ни чётная, ни нечётная.
- функция общего вида или ни чётная, ни нечётная.
Функция 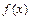 называется периодической на множестве
называется периодической на множестве  , если существует число
, если существует число 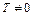 (период функции), такое, что для всех
(период функции), такое, что для всех 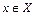 выполняется условие:
выполняется условие: 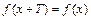 . Наименьшее число
. Наименьшее число  называется основным периодом.
называется основным периодом.
Функция 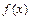 называется монотонно возрастающей (убывающей) на множестве
называется монотонно возрастающей (убывающей) на множестве  , если большему значению аргумента
, если большему значению аргумента 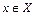 соответствует большее (меньшее) значение функции
соответствует большее (меньшее) значение функции 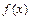 .
.
Функция 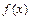 называется ограниченной на множестве
называется ограниченной на множестве  , если существует число
, если существует число  , такое, что для всех
, такое, что для всех 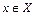 выполняется условие:
выполняется условие:  . В противном случае функция - неограниченная.
. В противном случае функция - неограниченная.
Обратной к функции 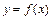 ,
, 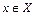 ,
,  называется такая функция
называется такая функция 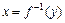 , которая определена на множестве
, которая определена на множестве  и каждому
и каждому
 ставит в соответствие такое
ставит в соответствие такое 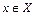 , что
, что  . Для нахождения функции
. Для нахождения функции 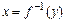 , обратной к функции
, обратной к функции 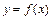 , нужно решить уравнение
, нужно решить уравнение  относительно
относительно 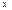 . Если функция
. Если функция 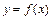 ,
, 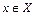 является строго монотонной на
является строго монотонной на  , то она всегда имеет обратную, при этом, если функция возрастает (убывает), то обратная функция также возрастает (убывает).
, то она всегда имеет обратную, при этом, если функция возрастает (убывает), то обратная функция также возрастает (убывает).
Функция 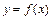 , представляемая в виде
, представляемая в виде 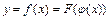 , где
, где 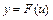 ,
,  - некоторые функции такие, что область определения функции
- некоторые функции такие, что область определения функции 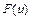 содержит всё множество значений функции
содержит всё множество значений функции  , называется сложной функцией независимого аргумента
, называется сложной функцией независимого аргумента 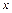 . Переменную
. Переменную  называют при этом промежуточным аргументом. Сложную функцию
называют при этом промежуточным аргументом. Сложную функцию 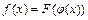 называют также композицией функций
называют также композицией функций 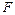 и
и  , и пишут:
, и пишут: 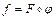 .
.
|
|
|
Основными элементарными функциями считаются: степенная функция 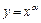 , показательная функция
, показательная функция  (
(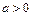 ,
, 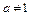 ), логарифмическая функция
), логарифмическая функция  (
(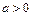 ,
, 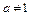 ), тригонометрические функции
), тригонометрические функции 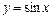 ,
, 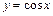 ,
, 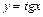 ,
, 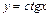 , обратные тригонометрические функции
, обратные тригонометрические функции  ,
, 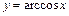 ,
,  ,
,  . Элементарной называется функция, полученная из основных элементарных функций конечным числом их арифметических операций и композиций.
. Элементарной называется функция, полученная из основных элементарных функций конечным числом их арифметических операций и композиций.
Если задан график  функции
функции 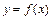 ,
, 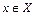 , то построение графика функции
, то построение графика функции 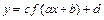 сводится к ряду преобразований (сдвиг, сжатие или растяжение, отображение) графика
сводится к ряду преобразований (сдвиг, сжатие или растяжение, отображение) графика  :
:
1) преобразование 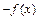 симметрично отображает график
симметрично отображает график  , относительно оси
, относительно оси  ; 2) преобразование
; 2) преобразование  симметрично отображает график
симметрично отображает график  , относительно оси
, относительно оси 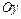 ; 3) преобразование
; 3) преобразование  сдвигает график
сдвигает график  по оси
по оси  на
на 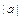 единиц (
единиц (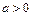 - вправо,
- вправо, 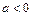 - влево); 4) преобразование
- влево); 4) преобразование 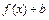 сдвигает график
сдвигает график  по оси
по оси 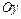 на
на 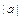 единиц (
единиц (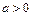 - вверх,
- вверх, 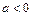 - вниз); 5) преобразование
- вниз); 5) преобразование 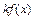 график
график  вдоль оси
вдоль оси 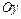 растягивает в
растягивает в  раз, если
раз, если 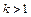 или сжимает в
или сжимает в 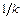 раз, если
раз, если 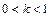 ; 6) преобразование
; 6) преобразование  график
график  вдоль оси
вдоль оси  сжимает в
сжимает в  раз, если
раз, если 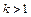 или растягивает в
или растягивает в 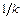 раз, если
раз, если 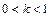 .
.
Последовательность преобразований при построении графика функции 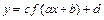 можно представить символически в виде:
можно представить символически в виде:
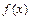







 .
.
Примечание. При выполнении преобразования 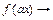
 следует иметь в виду, что величина сдвига вдоль оси
следует иметь в виду, что величина сдвига вдоль оси  определяется той константой, которая прибавляется непосредственно к аргументу
определяется той константой, которая прибавляется непосредственно к аргументу 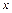 , а не к аргументу
, а не к аргументу 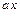 .
.
Графиком функции 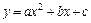 является парабола с вершиной в точке
является парабола с вершиной в точке  , ветви которой направлены вверх, если
, ветви которой направлены вверх, если 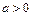 или вниз, если
или вниз, если 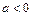 . Графиком дробно-линейной функции
. Графиком дробно-линейной функции 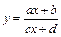 является гипербола с центром в точке
является гипербола с центром в точке 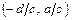 , асимптоты которой проходят через центр, параллельно осям координат.
, асимптоты которой проходят через центр, параллельно осям координат.
В некоторых случаях при построении графика функции целесообразно разбить её область определения на несколько непересекающихся промежутков и последовательно строить график на каждом из них. Например, при построении графика функции, в аналитическое выражение которой входит функция  , следует выделить и рассмотреть отдельно промежутки, на которых выражение под знаком модуля не меняет знак.
, следует выделить и рассмотреть отдельно промежутки, на которых выражение под знаком модуля не меняет знак.
График функции 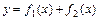 можно построить, предварительно построив графики функций
можно построить, предварительно построив графики функций 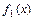 и
и 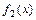 , а затем сложив их ординаты при одинаковых значениях
, а затем сложив их ординаты при одинаковых значениях 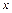 .
.
|
|
|
Тема 8. Предел функции. Эквивалентные функции.
Число  называется пределом функции
называется пределом функции 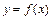 при
при 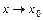 (или в точке
(или в точке  ), и пишут
), и пишут  , если для любого числа
, если для любого числа 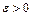 найдётся число
найдётся число  такое, что при всех
такое, что при всех 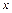 , удовлетворяющих условию
, удовлетворяющих условию 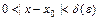 , выполняется неравенство
, выполняется неравенство 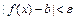 .
.
Число  называется пределом функции
называется пределом функции 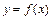 при
при 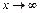 , и пишут
, и пишут 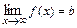 , если для любого числа
, если для любого числа 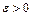 найдётся число
найдётся число  такое, что при всех
такое, что при всех 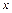 , удовлетворяющих условию
, удовлетворяющих условию  , выполняется неравенство
, выполняется неравенство 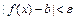 .
.
Рассматривают также односторонние пределы функций:  ,
, 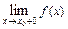 ,
, 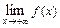 ,
, 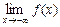 , где
, где 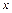 стремится к
стремится к  ,
,  ,
,  или только с левой стороны или только с правой стороны.
или только с левой стороны или только с правой стороны.
Основные утверждения, используемые для вычисления пределов функций при 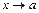 (в дальнейшем
(в дальнейшем  - или число
- или число  или символ
или символ 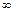 ):
):
1) Если 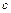 - постоянная величина, то
- постоянная величина, то 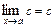 .
.
2) Если существуют конечные пределы 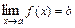 ,
, 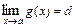 , то:
, то:
а) 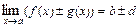 ; б)
; б) 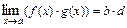 ;
;
в) 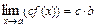
 ; г)
; г) 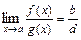 , если
, если 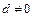 .
.
При вычислении пределов постоянно пользуются и тем, что для любой основной элементарной функции 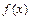 и точки
и точки  из её области определения справедливо соотношение
из её области определения справедливо соотношение 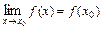 .
.
Функция 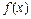 называется бесконечно большой при
называется бесконечно большой при 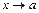 , если
, если  . Функция
. Функция 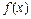 называется бесконечно малой при
называется бесконечно малой при 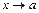 , если
, если 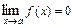 .
.
Основные утверждения для бесконечно больших функций, используемые для вычисления пределов при 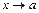 :
:
1) Если  , то
, то  ,если
,если  , то
, то 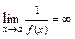
2) Если  и
и 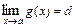 , то
, то 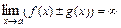 .
.
3) Если  и
и  , то
, то 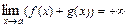 .
.
4) Если  и
и  , то
, то  .
.
5) Если 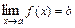 и
и 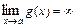 , то
, то  .
.
6) Если  и
и  , то
, то  .
.
Если непосредственное применение свойств конечных пределов и бесконечно больших функций приводит к неопределённым выражениям, символически обозначаемым: 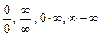 , то для вычисления предела – «раскрытия неопределённости» - преобразовывают выражение так, чтобы получить возможность его вычислить.
, то для вычисления предела – «раскрытия неопределённости» - преобразовывают выражение так, чтобы получить возможность его вычислить.
Первым замечательным пределом называется предел: 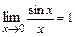 . Следствиями из него являются пределы:
. Следствиями из него являются пределы:
|
|
|
|
|
Дата добавления: 2014-12-08; Просмотров: 394; Нарушение авторских прав?; Мы поможем в написании вашей работы!