Пружинний, математичний і фізичний маятники

Пружинний маятник – це тіло масою 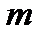, яке підвішене на невагомій абсолютно пружній пружині і здійснює гар­ монічні коливання під дією пружної сили , де 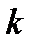– коефіцієнт пружності, який у випадку пружини називається жорсткістю (рис. 25). На тіло діє і сила тяжіння .

Запишемо основне рівняння динамі­ки для цього випадку:

,

де - статична деформація пружини під дією сила тяжіння mg.

Позначимо 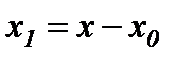і, враховую­чи, що , бо 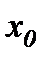не залежить від часу, знайдемо рівняння руху тіла:

, .

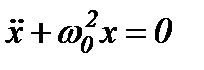де .

Отже, пружинний маятник здійснює вільні гармонічні коливання за законом

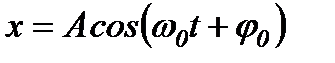
з власною циклічною частотою

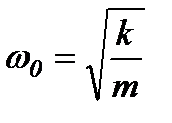
і періодом

.

Період коливань Т не залежить від амплітуди А.

Ця формула справедлива для пруж­них коливань в межах, в яких виконується закон Гука, та коли маса пружини мала порівняно з масою тіла.

Потенціальна енергія пружинного маятника дорівнює:

,

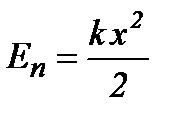а кінетична:

.

Математичним маятником називається матеріальна точка, яка підвішена на невагомій і нерозтяжній нитці. На практиці математичним маятником можна вважати важке тіло, яке підвішене на легенькій нитці, довжина якої набагато більша, ніж розміри тіла (рис. 26). Якщо відхилити маятник з положення рівноваги так, щоб нитка утворювала кут 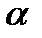з вертикаллю, то він почне коливатися у вертикальній площині під дією сили тяжіння .

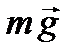Сила, що повертає математичний маятник у положення рівноваги, є складо­вою його сили тяжіння :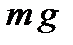

.

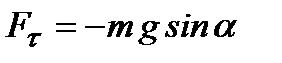Складова зрівноважується си­лою натягу нитки .

Для малих кутів відхилення можна замінити кутом 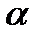, а дугу, вздовж якої рухається маятник, можна вважати відрізком прямої. Силу що повертає маят­ник до положення рівноваги, можна вва­жати квазіпружною силою:

.

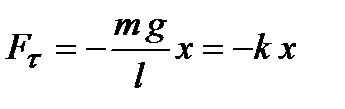Отже, малі коливання математично­го маятника – гармонічні.

Період цих коливань дорівнює:

.

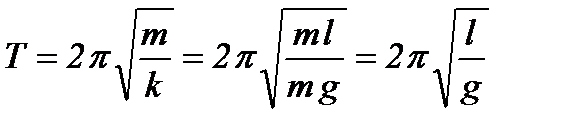Період малих коливань математич­ного маятника не залежить від амплітуди коливань.

Математичний маятник зберігає площину, в якій він коливається.

Спостереження над коливаннями маятників використовуються для визна­чення прискорення 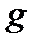сили тяжіння.

Фізичний маятник – абсолютно тверде тіло, що здійснює коливання під дією сили тяжіння навколо горизонтальної осі О, яка не проходить через його центр мас С (рис. 27).

Нехай маятник відхилено з положення рівноваги на невеликий кут 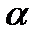. Складова сили тяжіння маятника 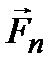, напрямлена вздовж осі , зрівноважується реакцією осі . Складова 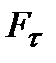, яка перпендикулярна до 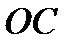, намагається повернути маятник у положення рівноваги.

Відповідно до рівняння динаміки обертального руху твердого тіла момент М обертальної сили 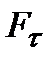можна записати у вигляді:

,

де J - момент інерції маятника відносно осі, що проходить через точку O, l - відстань між точкою підвісу і центром мас маятника, 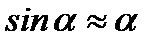відповідає малим коливанням маятника. Тоді

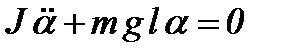або .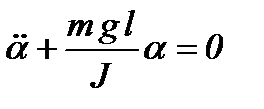

Позначивши

,

отримаємо рівняння

.

Розв’язок цього рівняння такий:

.

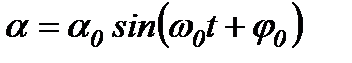При малих коливаннях фізичний маятник здійснює гармонічні коливання з частотою і періодом

,

де 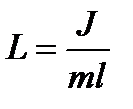- зведена довжина фізичного маятника.

Точка на продовженні прямої ОС, що знаходиться від осі підвісу на від­стані зведеної довжини L, називається центром гойдання фізичного маятника.

Точка підвісу O і центр гойдання мають властивість спряженості: якщо вісь підвісу проходить через центр гойдання, то точка O попередньої осі підвісу стане новим центром гойдання і період гойдання фізичного маятника не зміниться.

За теоремою Штейнера маємо:

,

де 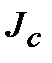- момент інерцій маятника відносно осі, що проходить через центр мас. Отже,

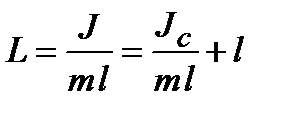, тому .

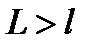Порівнюючи формули

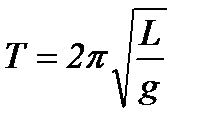і ,

бачимо, що якщо зведена довжина 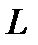фізичного маятника дорівняє довжині 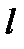математичного маятника, то їх періоди коливань одинакові.

Отже, зведена довжина фізичного маятника – це довжина такого матема­тичного маятника, період коливання якого дорівнює періоду коливань даного фізич­ного маятника.

Формулу для періоду Т математичного маятника можна отримати з виразу

,

якщо розглядати математичний маятник як окремий випадок фізичного, в якому вся маса зосереджена в центрі мас C на віддалі L від підвісу, що дорівнює довжині l нитки математичного маятника. Тоді 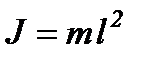і маємо 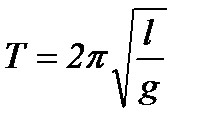. В загальному випадку період коливань математичного маятника визначається формулою:

,

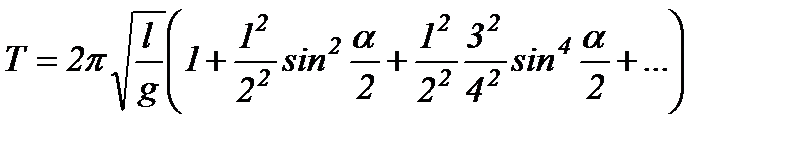де 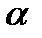- максимальний кут відхилення маятника.

Дата добавления: 2014-11-29