Властивості мішаного добутку

Мішаний добуток векторів

Означення мішаного добутку. Мішаним добутком трьох векторів 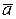, , 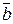називається число, отримане наступним чином: векторний добуток 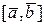множимо скалярно на вектор .

Мішаний добуток позначається .

Отже,

.

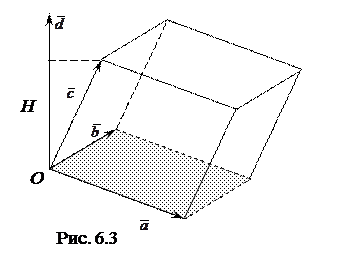
Геометричний зміст мішаного добутку. Побудуємо паралелепіпед, ребрами якого є вектори 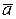, , 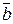(рис 6.3).

Маємо:

, ,

де 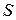– площа паралелограма, побудованого на векторах , ;

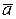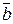для правої трійки векторів 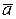, , 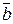і 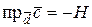для лівої трійки, де – висота паралелепіпеда.

Отримуємо

,

тобто

,

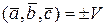де – об’єм паралелепіпеда, утвореного векторами , , .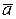

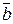Таким чином, модуль мішаного добутку трьох некомпланарних векторів чисельно рівний об’єму паралелепіпеда, ребрами якого є ці вектори: .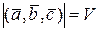

1. Мішаний добуток не змінюється при циклічній перестановці його множників: .

Дійсно, в цьому випадку не змінюється ні об’єм паралелепіпеда, ні орієнтація векторів.

2. .

Доведення. Так як за властивістю 1 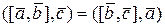і скалярний добуток не зміниться при перестановці векторів, тоб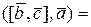то , то .

3. , , .

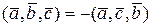Дійсно, при перестановці довільних двох векторів, враховуючи властивості 1, 2, переставляються множники векторного добутку, тому знак змінюється на протилежний.

4. Три ненульові вектори 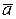, , 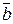компланарні тоді і тільки тоді, коли їх мішаний добуток рівний нулю.

Доведення. Якщо 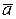, , 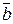компланарні, то вектор 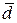= 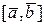перпендикулярний до площини, в якій лежать вектори 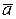, 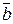і , а отже , тому , тобто .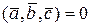

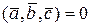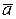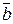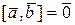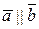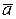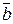Якщо і вектори , , – ненульові, то або вектор , а отже і , , – компланарні, або 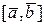= , а отже 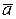, , 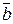– компланарні.

Мішаний добуток в координатній формі. Нехай в декартовій прямокутній системі координат задані вектори , , або, що те ж саме, , , .

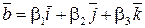Так як згідно (6.12)

,

то скалярний добуток 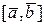на рівний

.

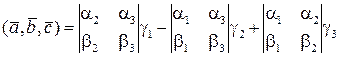Отриману формулу можна записати у вигляді

. (6.13)

Приклад 6.11. Вияснити, яка орієнтація трійки векторів , , .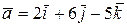

Розв’язок. Згідно (6.13)

,

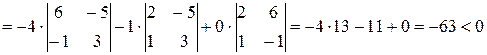тому вектори 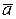, , 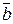мають ліву орієнтацію. t

Приклад 6.12. Перевірити, чи компланарні вектори , , .

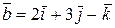Розв’язок. Так як

,

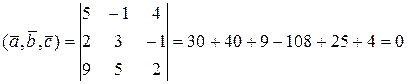то вектори 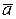, , 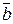– компланарні. t

Приклад 6.13. Знайти об’єм піраміди , якщо , , , .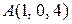

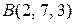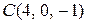Розв’язок. Знайдемо вектори , , :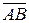

, , .

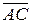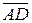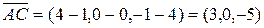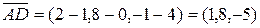Відомо, що , де – об’єм паралелепіпеда, ребрами якого є вектори 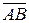, , 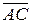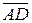. Отже

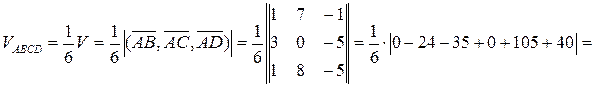
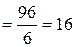(куб. од.) t

Теоретичні питання

6.1. Що називається скалярним добутком двох векторів?

6.2. Як виражається скалярний добуток через проекції одного вектора на інший?

6.3. Які властивості скалярного добутку?

6.4. Як виражається скалярний добуток через координати векторів в декартовій системі координат?

6.5. Як виражається довжина вектора через його координати?

6.6. Як виражається відстань між двома точками через їх координати?

6.7. Чому рівний кут між двома ненульовими векторами?

6.8. Яка умова ортогональності двох векторів?

6.9. Що називається напрямними косинусами вектора?

6.10. Що називається векторним добутком двох векторів?

6.11. Який геометричний зміст векторного добутку?

6.12. Які властивості векторного добутку?

6.13. Як виражається векторний добуток через координати векторів в декартовій системі координат?

6.14. Що називається мішаним добутком трьох векторів?

6.15. Який геометричний зміст мішаного добутку?

6.16. Які властивості мішаного добутку?

6.17. Як виражається мішаний добуток через координати векторів в декартовій системі координат?

Задачі та вправи

6.1. Знайти , якщо , , , , .

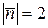6.2. Дано трикутник з вершинами в точках , , 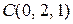. Знайти проекцію сторони на сторону .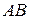

6.3. Знайти кут між векторами 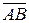і 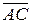, якщо , , .

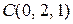6.4. Знайти , якщо , , .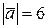

6.5. Знайти напрямні косинуси вектора .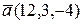

6.6. Знайти , якщо , , , , .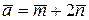

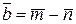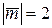6.7. Знайти площу паралелограма, побудованого на векторах і .

6.8. Знайти мішаний добуток векторів , , 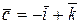. Вияснити, яка орієнтація трійки векторів , , .

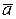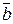6.9. Знайти об’єм паралелепіпеда, побудованого на векторах , , .

6.10. Перевірити, чи лежать точки 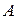, , 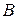, 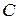в одній площині:

а) , , , ;

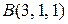б) , , , .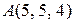

Дата добавления: 2014-11-29