Сопряжения

Практическая работа №8

На рис. 1 показаны детали машин. Мы видим, как в их контуре прямая линия плавно переходит в дугу окружности.

Плавный переход одной линии в другую называется сопряжением ( рис. 1).

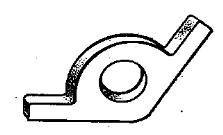
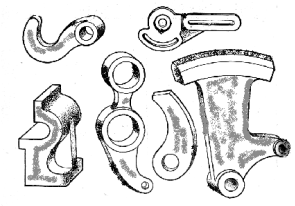
Рисунок 1. Форма детали

Бывает сопряжение одной прямой с другой прямой, прямой с кривой, одной кривой с другой кривой. Одна линия переходит в другую по дуге окружности. Эта дуга называется дугой сопрягающей окружности (рис. 2). Радиус этой окружности – радиус сопряжения. Центр этой окружности – центр сопряжения. Точка, где одна линия переходит в другую – точка сопряжения.

Сопряжение прямой линии и окружности и сопряжение окружности с окружностью бывает внешнее, внутреннее, смешанное.

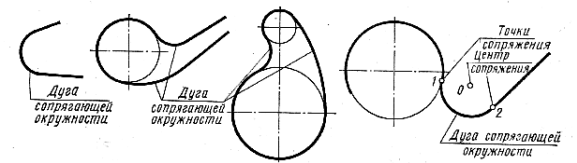
Рисунок 2

Внешнее сопряжение ( рис.3,а.). Сопрягаются две окружности. Их центры лежат вне сопрягающей окружности. Такое сопряжение называется внешним.

Внутреннее сопряжение (рис. 3,б). Сопрягаются две окружности. Их центры лежат внутри сопрягающей окружности. Та кое сопряжение называется внутренним.

Смешанное сопряжение (рис. 3,в) Сопрягаются две окружности. Центр одной окружности лежит вне сопрягающей окружности, центр другой окружности лежит внутри сопрягающей окружности. Такое сопряжение называется смешанным.

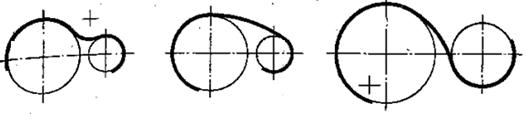
а) внешнее б) внутреннее в) смешанное

сопряжение сопряжение сопряжение

Рисунок 3. Виды сопряжений

Точки сопряжения зачастую имеют большое значение при проектировании и изготовлении многих изделий, поэтому на учебных чертежах они должны быть определены соответствующими линиями построения,как это сделано на рис.4

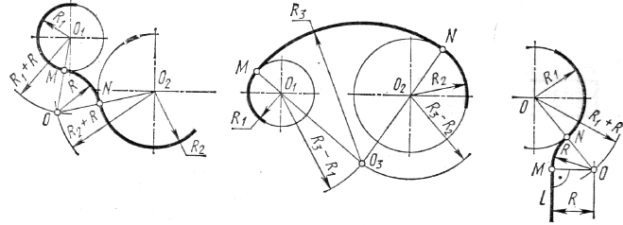
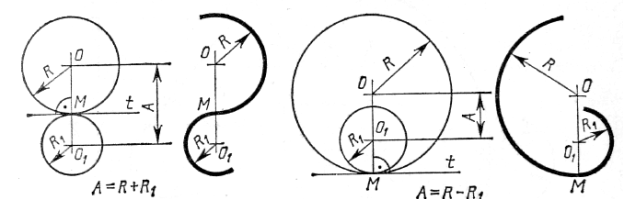
Рисунок 4. Построение сопряжений

Задача 1. Сопряжение сторон острого угла дугой окружности заданного радиуса R Расстояние от центра сопряжения до каждой стороны угла равно радиусу сопряжения R. Чтобы найти центр сопряжения, проводим две вспомогательные прямые, параллельные каждой стороне угла на расстоянии R от них. Эти вспомогательные прямые пересекаются в точке О. Точка О есть центр сопряжения. Чтобы найти точки сопряжения, из точки О опускаем перпендикуляры на стороны угла. Точки 1 и 2 —это точки сопряжения. Из центра сопряжения О проводим сопрягающую дугу радиуса R от точки 1 до точки 2.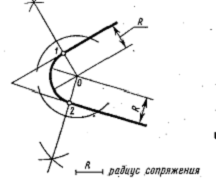
Задача 2. Сопряжение сторон прямого угла дугой радиуса R Из вершины А прямого угла как из центра проводим Дугу радиуса R. Точки 1 и 2 пересечения этой дуги с каждой стороной угла — это точки сопряжения. Из центра 1 и центра 2 проводим дуги радиуса R. Дуги пересекаются в точке О. Точка О — это Центр сопряжения. Из него проводим дугу сопрягающей окружности.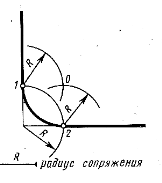
Задача 3. Построение сопряжения между прямой и дугой окружности. 1. Дана дуга окружности радиуса R 1 с центром O1 и прямая а 2. Проводим вспомогательную дугу радиуса (R1—R) из центра О1 3. Проводим вспомогательную прямую b1, параллельную прямой а, на расстоянии R Получаем точку О — центр сопряжения. 4. Проводим прямую O1O, получаем точку сопряжения 1. Из точки О опускаем перпендикуляр на прямую и, получаем точку сопряжения 2. Проводим сопрягающую дугу радиуса R от точки до точки 2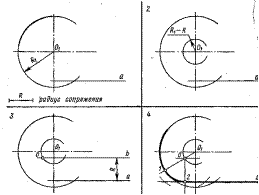
Задача 4. Построение смешанного сопряжения между двумя окружностями. 1.Даны две окружности радиуса R1 и R2. 2. Проводим вспомогательную дугу радиуса (R - R1) из центра O1 и дугу радиуса (R+R2) из центра 02. Получаем точку О — центр сопряжения. 3. Проводим прямую ОО1, получаем точку сопряжения 1. Проводим прямую ОО2, получаем точку сопряжения 2. 4. Проводим сопрягающую дугу радиуса R из центра О от точки 1 до точки 2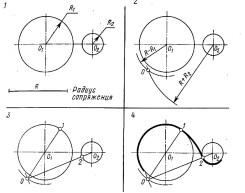

Дата добавления: 2014-12-10