Рекомендации по решению задачи № 1

Теоретические основы для выполнения задач

На практике часто возникает задача представления реального сложного детерминированного сигнала совокупностью более простых, хорошо изученных сигналов с последующим обратным восстановлением исходного сигнала. Это возможно выполнить с использованием известных базисных функций. Наибольшее применение находит представление сложных сигналов совокупностью простых с помощью обобщенного ряда Фурье:

,

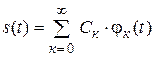где − реальный сигнал с ограниченной мощностью, представляемый функцией с интегрируемым квадратом в пространстве выбранного базиса; − коэффициенты разложения, несущие информацию о полезном сигнале ; − базисные функции.

При формировании и обработке сигналов часто приходится иметь дело с периодическими колебаниями сложной формы. Такие сигналы можно разложить в обобщенный ряд Фурье по ортогональным гармоническим функциям кратного аргумента (квадратурная или синусно-косинусная форма ряда Фурье):

;

где ; T – период; 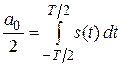– постоянная составляющая колебания (не зависящая от времени);

;

– проекции сигнала как вектора на косинусоидальные и синусоидальные координатные базисные оси.

Эквивалентная форма представления обобщенного ряда Фурье в базисе тригонометрических функций кратного аргумента имеет вид:

,

где – постоянная составляющая сигнала ;

– амплитуды гармонических составляющих разложения ряда; ; – частота первой (низшей) гармоники.

– начальная фаза k – й гармоники.

Совокупность и образуют амплитудный спектр сигнала , определяющий распределение амплитуд гармоник сигнала по спектру частот. Совокупность начальных фаз образует фазовый спектр сигнала , определяющий распределение фаз гармоник сигнала по спектру частот. При этом спектры амплитуд и фаз линейчатые. Операция по определению спектров амплитуд и фаз называется гармоническим анализом.

Спектр сигнала, как правило, изображается графически в виде спектра амплитуд и спектра фаз, которые представлены на рисунке 2.1.

Рис. 2.1. Спектры амплитуд и фаз периодического сигнала

Составляющие спектра называют гармониками. Каждая гармоника характеризуется своей амплитудой, частотой и начальной фазой. Например, аналитическая форма записи для первой гармоники будет иметь: 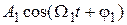; для второй гармоники – и т. д.

В данной задаче слушателям предлагается самостоятельно провести гармонический анализ исходного сигнала в виде периодической последовательности прямоугольных видеоимпульсов.

Итогом расчетов является определение спектров амплитуд и фаз, позволяющих в дальнейшем решить вопросы определения энергетической ширины спектра сигнала, его средней мощности и восстановления, с определенной степенью точности, первоначальной формы сигнала. Для более четкого уяснения свойств спектра амплитуд вводится понятие "огибающей" спектра амплитуд 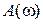, которая получается при устремлении к ¥ (т. е замены на ). В данной задаче огибающая представляет собой функцию вида . В конце расчетов определяется полная мощность сигнала и ширина спектра, занимаемая исходным сигналом при условии сохранения в нем заданного процента полной мощности.

Для передачи полной мощности требуется бесконечная ширина полосы частот, что реально невозможно. Поэтому на практике ограничивают полосу частот при передаче реальной мощности сигнала.

Полная мощность периодического колебания Р определяется выражением:

.

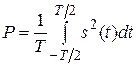Ee также можно определить с помощью равенства Парсеваля:

,

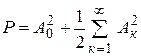используя бесконечное число гармоник.

Если число гармоник ограничить, тогда реальная ширина спектра становится конечной и в ней можно передать заданную мощность . Так, например, для передачи примерно 90 % полной мощности, достаточно использовать 2÷5 гармоник, при этом верхняя частота спектра равна частоте максимальной используемой гармоники. Таким образом

;

.

Дата добавления: 2014-12-10