Найдите обратную матрицу для матрицы

Подробнее о нахождении обратных матриц можно прочитать в [1] гл.4 [2], §15.

ЗАДАНИЕ №6

Задача №6 – задача решения системы линейных уравнений методом Гаусса.

Пусть задана система четырех линейных алгебраических уравнений с четырьмя неизвестными х₁,х₂,х₃,х₄

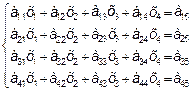
Требуется найти решение (х₁,х₂,х₃,х₄) этой системы.

Перед решением системы исследуем её на совместность. По теореме Кронекера – Капелли для совместности системы необходимо и достаточно, чтобы ранг основной А и расширенной А₁

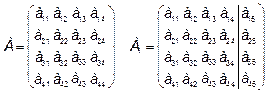
матриц совпадали

r (A)= r (A₁).

Система будет определенной, если ранг совместной системы равен числу неизвестных n

r (A)= n =4

Если , то первое уравнение системы заменяем на уравнение в котором а_i1= 1

По методу Гаусса с помощью эквивалентных преобразований над строками расширенную матрицу А₁ системы надо привести к матрице

В которой основная матрица А принимает треугольный вид 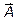, т.е. на главной диагонали матрицы А все элементы равны единице, ниже – нулю. На этом прямой ход метода Гаусса заканчивается.

В процессе обратного хода из матрицы 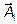находим значения неизвестных х_i, начиная с последней x₄=b₄₅ и до первой x₁=b ₁₅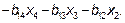

Одновременно с прямым ходом по методу Гаусса можно определить ранги r(A) и r(A₁)

Пример 1. Пусть задана система

Решение: Так как а ₁₁=0, I и IV (см. выше) уравнения системы меняем местами и записываем расширенную матрицу полученной системы

Выполняем последовательно следующие преобразования. В матрице каждый элемент I строки умножаем на (-2) и прибавляем к соответствующим элементам II строки; затем элементы I строки умножаем на (-1) и складываем с соответствующими элементами III строки. В результате получаем:

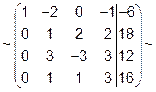
В полученной матрице элементы III строки делим на 3 и затем элементы II строки умножаем на (-1) и складываем с элементами соответственно III и IV строк:

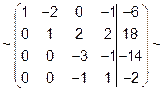
Элементы III и IV строк нашей матрицы меняем местами; элементы III строки делим на (-1), затем умножаем на (3) и складываем с элементами IV строки

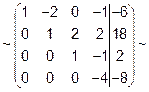
В этой матрице элементы IV строки делим на (-4)

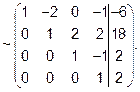
Полученной матрице соответствует система:

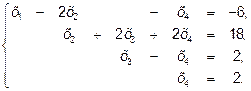
Из последнего уравнения системы х ₄=2; из III уравнения х₃ =2+ х ₄=2+2=4; из II уравнения х ₂=18-2 х ₄-2 х ₃= из I уравнения x₁=-6+2x₂+x₄=-6+2·6+2=8

Итак, решение системы равно (х₁,х₂,х₃,х₄)=(8;6;4;2).

Для избежания ошибок в решении студенту рекомендуется сделать проверку, подставив найденное решение (х₁,х₂,х₃,х₄) в каждое уравнение системы.

Найдем ранг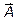и и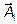

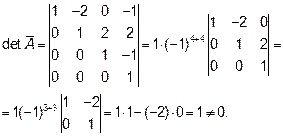
Таким образом, определитель матрицы 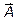треугольного вида равен произведению элементов, стоящих на главной диагонали.

Поскольку отличный от нуля определитель квадратной матрицы 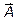имеет размерность 4 х 4, то ранг матрицы 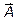равен r(А)=4.

В матрице вычеркиваем IV столбец и определяем ранг матрицы 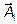в приведенном к треугольному виде:

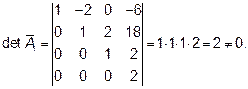
Отсюда r (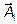)= 4.

Следовательно система совместна и определена.

Дата добавления: 2014-12-10