Решите самостоятельно следующие задачи

15.1.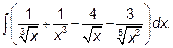

15.2.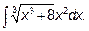

15.3.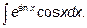

15.4.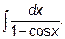

15.5.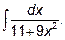

ЗАДАНИЕ №16

Следующая задача посвящена вычислению определённого интеграла, например:

Пример 1. Вычислить определенный интеграл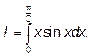

Решение: Определенный интеграл от любой непрерывный функции f(x) вычисляется по формуле Ньютона-Лейбница

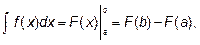
где F(x) – первообразная для f(x).

Геометрически определенный интеграл 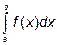представляет собой при 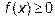площадь криволинейной трапеции, ограниченной кривой y=f(x), осью ox и прямыми x=a и x=b.

Проинтегрируем сначала соответствующий неопределенный интеграл по частям, положив u=x, dv=sin x dx.

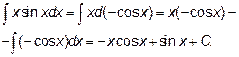
И по формуле Ньютона-Лейбница получим:

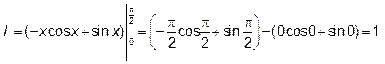
Пример 2. Найти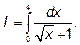

Решение: Находя первообразную с помощью замены переменной при вычислении определенного интеграла, не следует забывать, что, изменив переменную, придется изменить и ее пределы интегрирования.

Обозначим 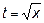, тогда 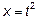, , 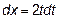но при x=0, t=0, а при x=4, t=2. Следовательно, в новом интеграле, относительно переменной t изменяются пределы интегрирования:

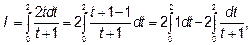
но так как dt=d(t+1)

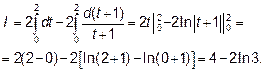
Пример 3. Найти площадь фигуры, ограниченной линиями: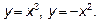

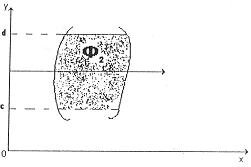
Площадь фигуры типа для которой 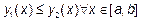, то есть, для правильной в направлении оси 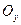фигуры на рисунке находятся по формуле

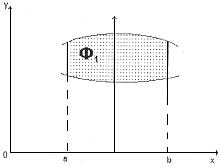
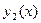
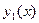
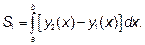
Для фигуры, правильной относительно оси 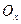на рисунке, то есть фигуры, которая ограничена

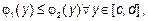
площадь находится по формуле

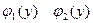
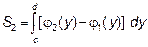
Решение: Решая совместно систему уравнений

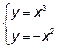
найдем абсциссы точек пересечения наших кривых 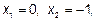следовательно, пределы интегрирования будут равны a=-1, b=0. Поскольку наша фигура является правильной, как относительно 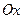, так и относительно 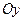, можно считать ее площадь по первой и по второй формуле. Будем считать по первой.

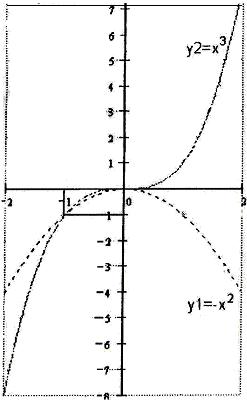
Тогда

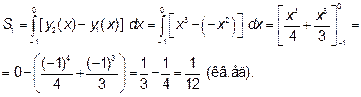
Подробнее об определённых интегралах можно прочесть в [1] гл.XIII, [4] гл.11 и найти похожие задачи в [3] гл.10

Самостоятельно решите следующие задачи:

Вычислить:

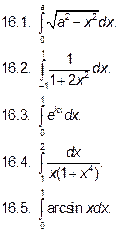
ЗАДАНИЕ №17

Далее разберём задачу о вычислении несобственных интегралов.

Определённый интеграл, который рассматривался в предыдущей задаче, вычисляется при двух предположениях:

1) отрезок интегрирования [a,b] конечен

2) подынтегральная функция на этом отрезке непрерывна

При таких предположениях интеграл называется собственным интегралом. В том случае, если отрезок интегрирования бесконечен или конечен, но подынтегральная функция на этом отрезке терпит разрыв, интеграл называется несобственным интегралом.

Несобственный интеграл с бесконечными пределами.

Пусть функция f(x) в промежутке 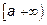непрерывна. Интегралом от f(x) в пределах между 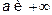называется предел интеграла, взятого от 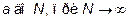, т.е.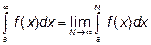

Это несобственный интеграл.

Если конечный предел в правой части существует, то несобственный интеграл называется сходящимся, а функция f(x) - интегрируемой на 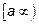. Если этот предел бесконечен или не существует, то интеграл называется расходящимся.

Интеграл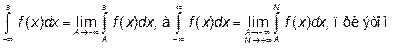

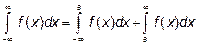для любого a.

Пример 1. Вычислить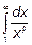

а) p¹1

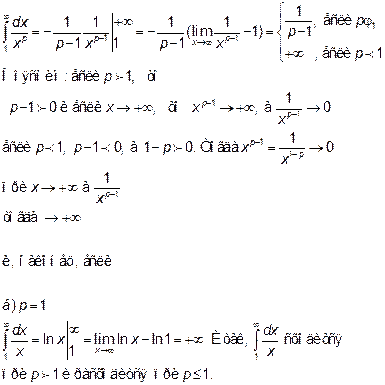
Пример 2. Вычислим несобственный интеграл 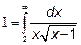или покажем, что он расходится.

Решение: Найдем неопределённый интеграл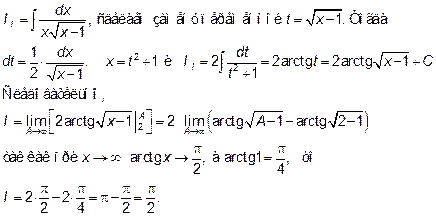

Итак, предел существует, значит, несобственный интеграл I сходится и равен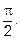

Интеграл 2-го рода.

Если в интеграле 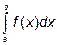функция f(x) неограниченно возрастает, то есть 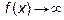когда x приближается к одному из пределов интегрирования. Когда это происходит при x®a, то .

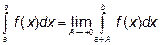Если подынтегральная функция перестаёт быть ограниченной внутри отрезка интегрирования, например в точке с то эту точку вырезают:

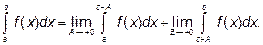
Пример 3. Вычислим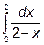

Решение: Когда x®2 подынтегральная функция 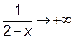. Точка x=2 особая.

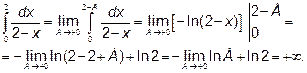
То есть интеграл расходящийся.

Подробнее с несобственными интегралами можно ознакомиться в[1]гл.XIV, [4] гл.11 и найти задачи на эту тему в [3] гл.10

Решите самостоятельно следующие задачи. Вычислить интегралы:

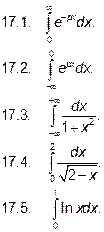
ЗАДАНИЕ №18

Разберём задачу вычислении приближённого значения определённых интегралов по формуле Симпсона.

Дата добавления: 2014-12-10