Следующие задачи решите самостоятельно

Найдите частные производные функций:

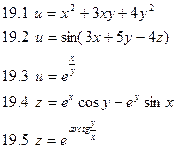
ЗАДАНИЕ №20

Продолжим рассмотрение функции нескольких переменных. Полное приращение функции определяется по формул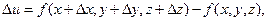е: где - приращения независимых переменных. По определению приращения независимых переменных и их дифференциалы dx, dy, dz – числа равные между собой.

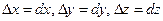. Полный дифференциал функции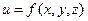

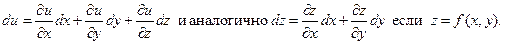(То есть в случае функции двух переменных).Полный дифференциал функции есть главная часть её приращения, линейная относительно 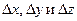, то есть 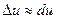или же 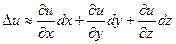для функции трёх переменных или 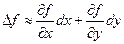для функции двух переменных. Подробнее (*)

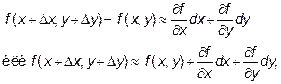где .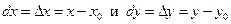

Подробнее о дифференциале функции нескольких переменных можно прочесть в [4] гл.8 или в [1] гл.15

Пример 1. Даны функции 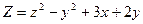и точка М(1,02;2,05). С помощью полного дифференциала вычислить приближенное значение функции в точке М и оценить относительную погрешность.

Решение: Приближенное значение некоторой функции f(x,y) в точке (x,y) с помощью полного дифференциала находится по формуле (*)

,

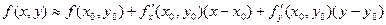где 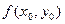, значение функции f(x,y) в точке .

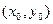Точка 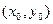подбирается таким образом, чтобы 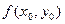легко вычислялось; 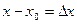, 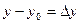приращение функции f(x,y) в точке 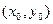по переменным x и y соответственно.

В качестве точки 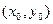возьмем точку N(1,2), так как значение x и y в точке N целые и точка N близка к данной точке M.

Тогда

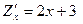в точке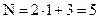

в точке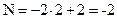

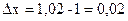
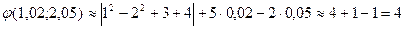
Вычислим точное значение

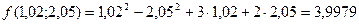
Итак, принимая вместо точного значения 3,9979 значение 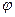, мы допускаем абсолютную погрешность 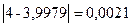или относительную погрешность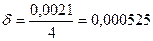

Решите самостоятельно следующие задачи:

20.1 Найти полное приращение и полный дифференциал функции

20.2 Найти полный дифференциал функции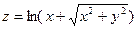

ЗАДАНИЕ №21

Следующая задача об экстремумах функций двух переменных и об отыскании наибольших и наименьших значений функции двух независимых переменных. Функция ограниченная и дифференцируемая в замкнутой области достигает в этой области своего наибольшего и наименьшего значения или во внутренних точках этой области, которые являются точками стационарности функции или на её границе. Для того, чтобы найти наибольшее и наименьшее значение функции, надо:

1) Найти стационарные точки функции, для чего следует решить систему уравнений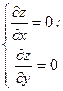

2) Вычислить в стационарных точках значения функции

3) Найти наибольшие и наименьшее значение функции на каждой линии, ограничивающей область;

4) Сравнить все полученные значения. Наибольшее из них будет наибольшим, а наименьшее – наименьшим значением функции в замкнутой области.

Пример 1. Найти наибольшее и наименьшее значение функции 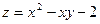в ограниченной замкнутой области D: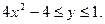

Решение: Точка 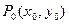являются точкой экстремума (максимума или минимума) функции z=f(x,y), если значение функции в этой точке соответственно больше или меньше значений, принимаемых ее в некоторой окрестности точки 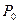, то есть при всех x и y достаточно близких к 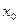и 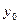. Точка P, координаты которой обращают в нуль обе частные производные функции f(x,y) называются стационарной точкой этой функции.

1. Найдем стационарные точки функции z(x,y)

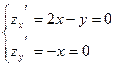
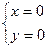
Стационарная точка y функции z одна. Это точка 0.

1. Входит ли точка (0,0) в область D? Построим эту область.

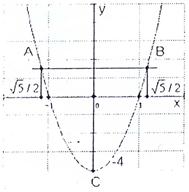
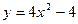- - парабола с вершиной в точке (0,-4). Точки пересечения с осью x: , ,

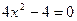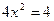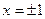
- y=0 – ось x.

Точка (0,0) входит в область D. Установим, является ли стационарная точка 0 точкой экстремума. Это делается так: Пусть 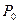стационарная точка функции z=f(x,y). Вычислим в этой точке

. .

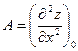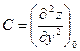
Если 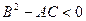, то функция f(x,y) имеет в точке 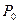экстремум:

max-при A<0 и min при A>0.

Если 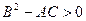, то точка 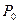не является точкой экстремума.

Если 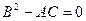, то требуется дополнительное исследование.

Исследуем нашу функцию z по формулам.

3.

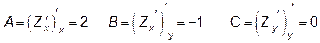
, точка (0,0) не является точкой экстремума.

4. Исследуем поведение функции на границе.

Так как Z не имеет ни max ни min, ее наибольшим и наименьшем значением является наибольшее и наименьшее из значений, принимаемых на границе.

Для того, чтобы найти наибольшее или наименьшее из значений, принимаемых на границе.

4а. Рассмотрим верхнюю границу y=1. На ней функция Z(x,1) превращается в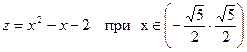

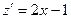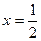, в этой точке возможен экстремум. Знак производной меняется с – на +, то есть в точке 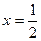- минимум z =-2.25

при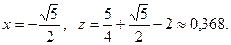

В точке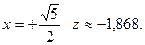

4б. Рассмотрим нижнюю границу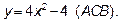

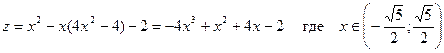
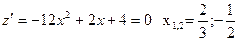
В точке 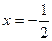производная меняет знак с - на +, следовательно, это точка минимума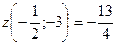

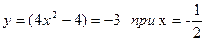
В точке 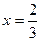производная меняет знак с + на -, следовательно, это точка максимума 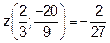. При 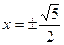функция z уже вычислялось. Видим, что от 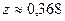функция убывает до 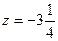, затем возрастает до 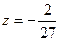а затем убывает до .

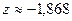То есть наименьшее значение для всей границы 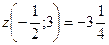, а наибольшее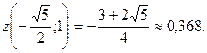

Ответ: Наибольшее значение функции z в замкнутой области D 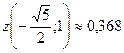, наименьшее .

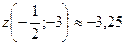Подробнее об этом можно почитать в [1] гл. XV, [4] гл.8, и найти аналогичные задачи в [3] гл.8

Решите самостоятельно следующие задачи:

21.1 Найдите наибольшее и наименьшие значение функции 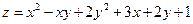в замкнутом треугольнике, ограниченном осями координат и прямой x+y+5=0

21.2 Найти наибольшее и наименьшее значения функции z=xy(x+y+1) в замкнутой области, ограниченной линиями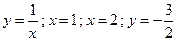

21.3 Доказать, что из всех треугольников, имеющих данный периметр 2p наибольшую площадь имеет равносторонний треугольник.

ЗАДАНИЕ №22

Следующая задача посвящена нахождению вектора – градиента для функции нескольких переменных.

Подробнее об этом можно прочесть в [4] гл.8 и [1]гл. XXVIII

вектор-градиент обозначается grad u или Ñu.

Пример 1. Даны функция трех переменных 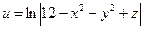, вектор 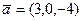и точка .

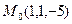Найти: 1) Grad u в точке M₀;

2) производную в точке M₀ по направлению вектора ;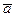

3) наибольшую крутизну поверхности u в точке M₀.

Решение:

1) Вектором градиентом функции трех переменных u(x,y,z) является вектор
grad 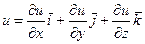(или 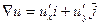в случае двух переменных)

Найдем частные произведения функции u:

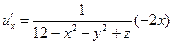
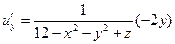
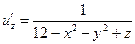
Из определения градиента следует, что эти частные производные являются проекциями вектора-градиента на оси координат. Вычислим значения частных производных в точке M_o.

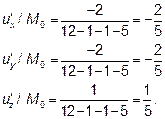
Следовательно вектор-градиент в точке M₀ имеет вид:

2) Производная по направлению вектора 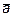вычисляется по формуле 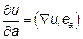, то есть равна скалярному произведению вектора градиента на единичный вектор, совпадающий по направлению с вектором .

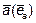Так как 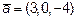, то его длина 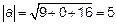и, следовательно, единичный вектор, совпадающий по направлению с 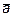, , 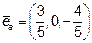используя формулу скалярного произведения в координатной форме 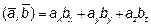, получим

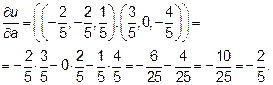
Итак производная функции u по направлению вектор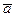а равна .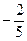

3) Поскольку |grad u| есть наибольшее значение производной 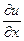в данной точке P, а направление grad u совпадает с направлением луча, выходящего из точки P, вдоль которого функция меняется быстрее всего, то направление градиента есть направление наискорейшего возрастания функции u(x,y,z)

|grad u| = .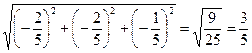

Решите самостоятельно следующие задачи:

22.1 Найти вектор-градиент функции 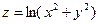в точке (1,1)

22.2 Найти производную функции 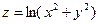в направлении вектора-градиента

Аналогичные задачи можно найти в [3] гл.8

ЗАДАНИЕ №23

Рассмотрим теперь интегрирование функций нескольких переменных.

Двойным интегралом от функции 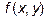по области D называется предел интегральной суммы при условии, что число элементарных областей n стремится к бесконечности, а наибольший из диаметров элементарных областей стремится к нулю:

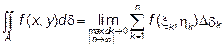
Если функция 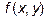непрерывна в замкнутой области D, то предел интегральной суммы существует и не зависит от способа разбиения области D на элементарные и от выбора точек Р_к

Если 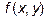>0 в области D, то двойной интеграл

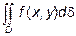
геометрически есть объём цилиндрического тела, ограниченного сверху поверхностью 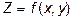, сбоку цилиндрической поверхностью с образующими, параллельными оси OZ, и снизу областью D плоскости ХОY.

Основные свойства интегралов

1.

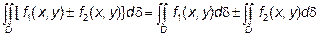
2. где С – постоянная

3. Если область интегрирования D разбита на две области D₁ и D₂, то

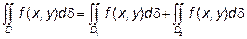
Различают два основных вида области интегрирования:

1. Область интегрирования D ограничена слева и справа прямыми х=а и х=в (a<в), а снизу и сверху непрерывными кривыми y=φ₁(x) и y=φ₂(x) 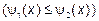, каждая из которых пересекается вертикальной прямой только в одной точке / рис.1/.

По такой области двойной интеграл вычисляется по формуле:

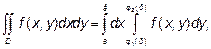
Причем сначала вычисляется внутренний интеграл 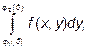в котором х считается постоянным.

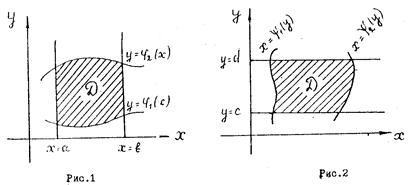
1. Область интегрирования D ограничена снизу и сверху прямыми y=c и y=d (c<d), а слева и справа непрерывными кривыми х=φ₁(y) и х=φ₂(y) каждая из которых пересекается горизонтальной прямой только в одной точке (рис. 2).

В такой области двойной интеграл вычисляется по формуле:

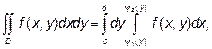
Причем сначала вычисляется интеграл 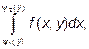в котором y считается постоянным.

Правые части формул называются двукратными или повторными интегралами. В более общем случае область интегрирования путем разбиения на части сводится к основным.

Подробнее о двойных и тройных кратных интегралах можно прочесть в [5] гл.14 и [1] гл XXVI

Пример 1. Вычислить двойной интеграл: .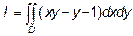

По области D: y=x², y=2-x². Область D изобразить на чертеже.

Решение: Изобразим область D. Кривые, задающие область D представляют собой параболы. Составив из их уравнений систему и решив её, найдём точки их пересечения.

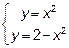
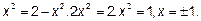
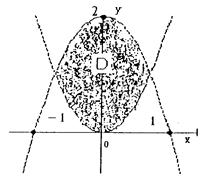Итак, точки пересечения парабол (1,1) и (-1,1). Изобразим область D в декартовой системе координат.

Двойной интеграл в декартовых координатах записывается так: 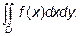В зависимости от вида области интегрирования двойной интеграл сводится к повторному по разным формулам.

Область D является областью первого вида, х изменяется от -1 до +1, у от у=х² до у=2-х², следовательно наш интеграл сводится к следующему повторному интегралу:

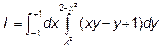
Возьмем внутренний интеграл, считая х – постоянным, то есть рассматривая его как обычный интеграл по переменной у.

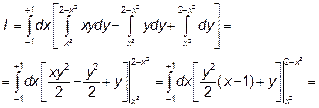
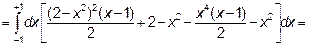
А затем внешний интеграл по переменной х

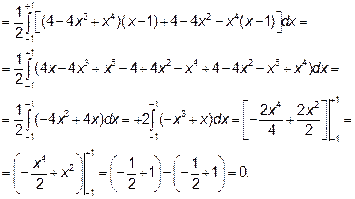
Пример 2. С помощью двойного интеграла найти объем тела, ограниченного поверхностями:

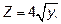x+y=4, x=0, Z=0.

Решение: Как было сказано, объем тела с помощью двойного интеграла выражается по формуле:

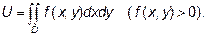
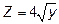- это цилиндрическая поверхность с образующими, параллельными оси ОХ.

Направляющей служит парабола, точнее одна ветвь параболы

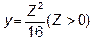
x+y=4 - это плоскость, параллельная оси OZ, пересекающая плоскость ХОУ по прямой,

заданной уравнением x+y=4. Построим ее на том же чертеже.

Уравнения Х=0 и Z=0 задают соответственно координатные плоскости ZOУ и ХОУ.

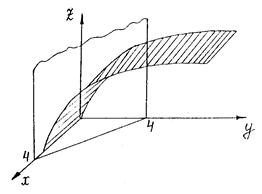
Итак, нетрудно себе представить, что тело ограничено сверху цилиндрической поверхностью 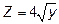, снизу плоскостью ХОУ, сбоку х=0 и x+y=4.

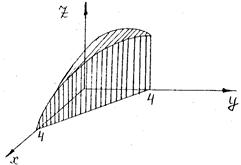
Необходимо построить область D.

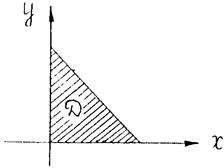
Область интегрирования D принадлежит одновременно и к первому и ко второму виду.

Будем рассматривать ее как область первого вида. Воспользуемся формулой для области первого вида.

Чтобы правильно расставить пределы интегрирования, нужно помнить, что пределами на внешнем интеграле могут быть только числа(пределы изменения Х), а на внутреннем, в общем случае, функции. Нужно уяснить, какой кривой ограничена область снизу, и какой – сверху, и записать соответственно правые части уравнений кривых, решенных относительно У, в качестве пределов интегрирования. В качестве подинтегральной функции 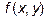пишем правую часть уравнения .

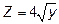Получим:

=

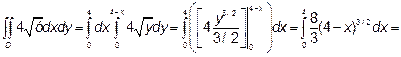
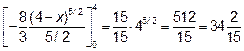
Ответ: .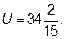

Решите самостоятельно следующие задачи:

23.1 Измените порядок интегрирования в двойном интеграле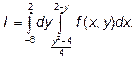

23.2 Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой

ЗАДАНИЕ №24

Следующая задача относится к вычислению тройного интеграла

Тройным интегралом от функции 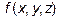по области Ư называется предел интегральной суммы при условии, что

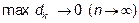, где d - диаметр частичной области разбиения

Для непрерывной в области U функции этот предел существует и не зависит от способа разбиения области U на элементарные и от выбора точек Р_к (теорема о существовании тройного интеграла).

Если 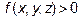в области U, то тройной интеграл 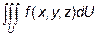физически есть масса тела, занимающего область U и имеющего переменную плотность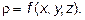

В частности, если 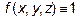, то тройной интеграл определяет объем области U,т.е.

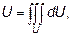
dU – элемент объёма.

Основные свойства тройных интегралов аналогичны свойствам двойных интегралов.

В декартовых координатах тройной интеграл обычно записывают в виде:

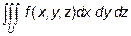
Вычисление тройного интеграла

Пусть область интегрирования U определяется неравенствами:

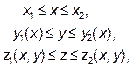
Где y₁(x), y₂(x), z₁(x, y), z₂(x, y) – непрерывные функции. Тогда тройной интеграл от функции 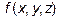по области U вычисляется по формуле:

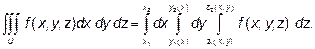
Интеграл стоящий в правой части формулы называется трехкратным. Он принципиально мало чем отличается от двукратного, добавляется лишь интегрирование еще по одной переменной.

Пример 1. Вычислить с помощью тройного интеграла объём тела, ограниченного

поверхностями

z=0, z=4-y², x²=2y.

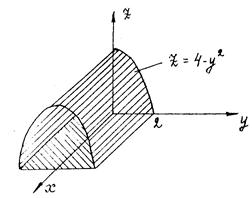Решение: Данное тело ограничено сверху цилиндрической поверхностью z=4-y² с образующими, параллельными оси ОХ, снизу плоскостью z=0 (координатная плоскость ХОУ).

Эти поверхности

пересекаются по

прямым:

у = -2 и у = +2

Тело U ограничено также цилиндрической поверхностью x²=2y с образующими, параллельными оси OZ

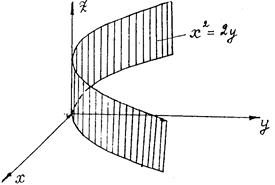
Поверхности, пересекаясь, образуют замкнутое тело, которое проецируется в область Д

плоскости ХОУ

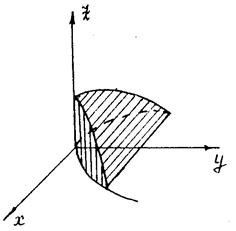
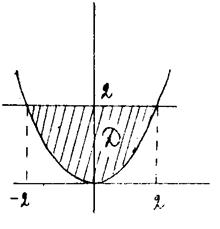
Для вычисления объёма воспользуемся формулами. Пределы интегрирования по Х и У расставятся в соответствии с областью Д (как в двухкратном интеграле), а пределами интегрирования по Z будут:

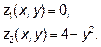
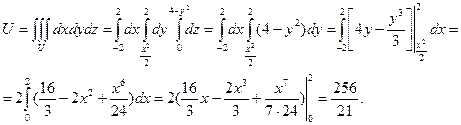
Получим

Ответ: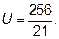

Дата добавления: 2014-12-10