Лекция по теме 1: Математика в современном мире. Математические модели в науке

План лекции:

1. Основные математические теории.

2. Основные методы математики.

3. Методы научных исследований.

4. Математические модели для обработки результатов эксперимента.

5. Функция как математическая модель реальных процессов.

Основные математические теории

До начала 17 в. математика – преимущественно наука о числах, скалярных величинах и сравнительно простых геометрических фигурах; изучаемые ею величины (длины, площади, объемы и пр.) рассматриваются как постоянные. К этому периоду относится возникновение арифметики, геометрии, позднее - алгебры и тригонометрии и некоторых частных приемов математического анализа. Областью применения математики являлись: счет, торговля, землемерные работы, астрономия, отчасти архитектура.

В 17 и 18 вв. потребности бурно развивавшегося естествознания и техники (мореплавания, астрономии, баллистики, гидравлики и т.д.) привели к введению в математику идей движения и изменения, прежде всего в форме переменных величин и функциональной зависимости между ними. Это повлекло за собой создание аналитической геометрии, дифференциального и интегрального исчислений. В 18 в. возникают и развиваются теория дифференциальных уравнений, дифференциальная геометрия и т.д. В 19-20 вв. математика поднимается на новые ступени абстракции. Обычные величины и числа оказываются лишь частными случаями объектов, изучаемых в современной алгебре; геометрия переходит к исследованию "пространств", весьма частным случаем которых является евклидово пространство. Развиваются новые дисциплины: теория функций комплексного переменного, теория групп, проективная геометрия, неевклидова геометрия, теория множеств, математическая логика, функциональный анализ и др. Практическое освоение результатов теоретического математического исследования требует получения ответа на поставленную задачу в числовой форме.

В связи с этим в 19-20 вв. численные методы математики вырастают в самостоятельную ее ветвь - вычислительную математику. Стремление упростить и ускорить решение ряда трудоемких вычислительных задач привело к созданию вычислительных машин. Потребности развития самой математики, "математизация" различных областей науки, проникновение математических методов во многие сферы практической деятельности, быстрый прогресс вычислительной техники привели к появлению целого ряда новых математических дисциплин, как например, теория игр, теория информации, теория графов, дискретная математика, теория оптимального управления.

Математика - область человеческого знания, изучающая математические модели, отражающие объективные свойства и связи. "Замечательно, - пишет В.А. Успенский, - что хотя математическая модель создается человеческим разумом, она, будучи создана, может стать предметом объективного изучения. Познавая ее свойства, мы тем самым познаем и свойства отраженной моделью реальности". Кроме того, математика дает удобные способы описания самых разнообразных явлений реального мира и тем самым выполняет роль языка науки. Наконец, математика дает людям методы изучения и познания окружающего мира, методы исследования как теоретических, так и практических проблем.

Математика (греч. mathematike, от mathema - знание, наука) наука, в которой изучаются пространственные формы и количественные отношения.

Современное понятиематематики - наука о математических структурах (множествах, между элементами которых определены некоторые отношения).

У представителей науки начала 19 века, не являющихся математиками, можно найти такие общедоступные определения математики.

«Чистая математика имеет своим объектом пространственные формы и количественные отношения действительного мира» (Ф. Энгельс).

«Математика – наука о величинах и количествах; все, что можно выразить цифрою, принадлежит математике. Математика может быть чистой и прикладной.

Математика делится на арифметику и геометрию; первая располагает цифрами, вторая - протяжениями и пространствами. Алгебра заменяет цифры более общими знаками, буквами; аналитика добивается выразить все общими формулами, уравнениями, без помощи чертежа» (В. Даль).

Современная математика насчитывает множество математических теорий: математическая статистика и теория вероятности, математическое моделирование, численные методы, теория групп, теория чисел, векторная алгебра, теория множеств, аналитическая и проективная геометрия, математический анализ и т.д.

Несмотря на то, что математических теорий достаточно много и они, на первый взгляд, могут и не иметь ничего общего, внутренняя эволюция математической науки упрочила единство ее различных частей и создала центральное ядро. Существенным в этой эволюции является систематизация отношений, существующих между различными математическими теориями; ее итогом явилось направление, которое обычно называют «аксиоматический метод». В теории, построенной в согласии с аксиоматическим методом, начинают с небольшого количества неопределяемых (первичных) понятий, с помощью которых образуются утверждения, называемые аксиомами.

Прочие понятия, изучаемые в теории, определяются через первичные, и из аксиом и определений выводятся теоремы. Теория становится рекурсивно структурированной, ее можно представить в виде матрешки, в которой понятия и их свойства как бы являются вложенными друг в друга. Каждая математическая теория является цепочкой высказываний, которые выводятся друг из друга согласно правилам логики, т.е. объединяющим началом математики является «дедуктивное рассуждение». Развитие математической теории в таком стиле - это первый шаг по направлению к ее формализации.

Открытие неевклидовой геометрии и создание теории множеств привели к перестройке всего здания математики и созданию совершенно новых ее отраслей. Важное значение приобрела в современной математике математическая логика. Методы математики широко используются в точном естествознании. Применение ее в биологии и общественных науках до последнего времени носило случайный характер. Создание (под непосредственным влиянием практики) таких отраслей, как линейное программирование, теория игр, теория информации, и появление электронных математических машин открывают здесь совершенно новые перспективы. Философские вопросы математики (характер и происхождение математической абстракции, ее особенности) всегда являлись ареной борьбы между материализмом и идеализмом. Особенно важное значение имеют философские вопросы, возникшие в связи с проблемами оснований математики.

Математика играет важную роль в естественнонаучных, инженерно-технических и гуманитарных исследованиях. Причина проникновения математики в различные отрасли знаний заключается в том, что она предлагает весьма четкие модели для изучения окружающей действительности в отличие от менее общих и более расплывчатых моделей, предлагаемых другими науками. Без современной математики с ее развитым логическими и вычислительным аппаратом был бы невозможен прогресс в различных областях человеческой деятельности. Математика является не только мощным средством решения прикладных задач и универсальным языком науки, но также и элементом общей культуры.

Основные методы математики

Математика представляет собой науку о количественных отношениях и пространственных формах действительного мира. В данной науке придается большое значение математическим методам, моделям, формулам, но эти методы,модели и формулы не могут заменить и подменить теоретического анализа сущности различных явлений и процессов. Проникновение математики и компьютеров, например, в педагогический анализ – объективный процесс. «Зрелость науки обычно измеряется тем, в какой мере она использует математику. Сама же математика не является наукой в эмпирическом смысле, но представляет собой формальную логическую, символическую систему, своего рода игру знаков и правил», - так начинает С.С. Стивенс свой капитальный труд Экспериментальная психология». Как же использовать математику? В настоящее время математические процедуры обязательно входят в такие разделы педагогики, как диагностика, педагогическая диагностика, квалиметрия, технология, педагогическая технология, дифференциальная педагогика, психодиагностика и др. Широко используется такой раздел высшей математики, как структурное моделирование, и такой раздел математической статистики, как дисперсионный анализ. Главное отличие отраслей педагогических знаний, использующих математические методы, от чисто описательных теорий заключается в том, что их предмет исследования может быть не только описан, но и измерен. Возможность измерения того или иного педагогического феномена, процесса, явления, свойства, характеристики, черты и т.д. открывает доступ для применения методов количественного анализа, а значит, и соответствующих математических и статистических процедур. Доказать истинность можно только в таком педагогическом эксперименте, который позволяет, во-первых, провести количественное измерение, в во-вторых, применить математическую статистику и математические методы. Их адекватное применение позволит:

1) доказывать правильность и обоснованность педагогических приемов и методов;

2) строго обосновывать экспериментальные планы;

3) обобщать данные, полученные в экспериментах;

4) находить различного рода зависимости между экспериментальными данными;

5) выявлять наличие существенных различий между группами испытуемых (например, экспериментальными и контрольными);

6) выявлять наличие взаимосвязи между изучаемыми переменными;

7) строить статистические предсказания;

8) избегать многих логических и содержательных ошибок как в постановке теоретических постулатов, так и в интерпретации результатов эксперимента и многое другое.

Происходит обогащение обработки информации на основе анализа, развивается теория комплексного анализа, имитационное моделирование для анализа конкретных педагогических ситуаций.

Систематизировать применяемые в педагогическом анализе математические методы можно по различным признакам. Наиболее целесообразной представляется классификация математических методов по содержанию метода, т.е. по принадлежности к определенному разделу современной математики. Сформулированная математическая задача может быть решена одним из наиболее разработанных математических методов. Выделение классических методов математического анализа обусловлено тем, что они применяются не только в рамках других методов, например методов математической статистики и математического программирования, но и отдельно. Так, факторный анализ изменения многих показателей может быть осуществлен при помощи дифференцирования и других разработанных на базе дифференцирования методов.

Широкое распространение имеют методы математической статистики и теории вероятностей. Эти методы применяются в тех случаях, когда изменение анализируемых показателей можно представить как случайный процесс.

Статистические методы как основное средство изучения массовых, повторяющихся явлений играют важную роль в прогнозировании исследуемых явлений. Когда связь между анализируемыми характеристиками не детерминированная, а стохастическая, то статистические и вероятностные методы есть практически единственный инструмент исследования. Наибольшее распространение из математико-статистических методов получили методы множественного и парного корреляционного анализа.

Для изучения одномерных статистических совокупностей используются вариационный ряд, законы распределения, выборочный метод. Для изучения многомерных статистических совокупностей применяют корреляции, регрессии, дисперсионный и факторный анализ.

Математическое программирование – важный раздел современной прикладной математики. Методы математического (прежде всего линейного) программирования служат основным средством решения задач оптимизации. Под исследованием операций подразумеваются разработка методов целенаправленных действий (операций), количественная оценка полученных решений и выбор наилучшего из них.

Эвристические методы (решения) – это неформализированные методы решения аналитических задач, связанные с опросом и экспертными оценками специалистов, высказывающих свое мнение на основе интуиции, опыта, с математической обработкой разных мнений для нахождения правильного решения.

Факторный анализ мы можем также применить для обработки информации, полученной в ходе педагогического исследования. Таким образом, математические методы и методы математической статистики в руках педагога могут и должны быть мощным инструментом, позволяющим исследователю не только успешно лавировать в море экспериментальных данных, но и прежде всего, способствовать становлению его объективного, строго научного мышления.

Методы научных исследований

В гуманитарных науках чаще всего используются следующие методы: документальный, анкетирования, моделирования, экспериментальный, экспертный, математико-статистический, кибернетический, метод наблюдений. Дадим им краткую характеристику.

Метод наблюдений предполагает фиксацию результатов наблюдения, проведение собеседований. Документальный метод основан на изучении различных документов и материалов по проблеме исследования: нормативных актов, учебных планов и программ, контрольных работ, анкетных данных обучаемых, сведений об учебном заведении и т.п.

В методе анкетирования используются специально разработанные анкеты, которые должны быть валидными для цели анкетирования, обладать измерительной и статистической надежностью.

Моделирование как метод исследования объектов познания на их моделях достаточно широко используется в научных исследованиях. В гуманитарных исследованиях используются мысленные, знаковые модели, аналоговое, имитационное, стохастическое, математическое, компьютерное и другие разновидности моделирования.

Эскпериментальный метод исследования должен опираться на теорию планирования эксперимента. С учетом специфики изучаемых объектов. Существует довольно обширная научная, методическая и справочная литература по организации экспериментальных исследований.

Наиболее перспективным и более объективным из множества экспертных методов является метод групповых экспертных оценок.

К математико-статистическим методам исследования обычно относят математические приемы из таких разделов математики, как математическая статистика и теория вероятностей, дисперсионный и корреляционный анализ.

Что касается кибернетических методов исследования, то под ними понимается весь комплекс методов, реализуемых на базе ЭВМ с соответствующим программным обеспечением типа: автоматизированные информационно-поисковые системы, автоматизированные обучающие системы, экспертные системы. К этой категории методов следует отнести рейтинговые и мониторинговые системы, тестовые технологии (психодиагностика, дидактометрия), реализуемые с помощью компьютерной техники.

Математические модели для обработки результатов эксперимента

Одним из наиболее плодотворных методов математического познания действительности является метод построения математических моделей изучаемых реальных объектов или объектов, уже описанных в других областях знаний с целью их глубокого изучения и решения всех возникающих в этих реальных ситуациях задач с помощью математического аппарата.

Математическая модель - это приближенное описание какого-либо класса явлений, выраженное на языке какой-нибудь математической теории (с помощью алгебраических функций или их систем, дифференциальных или интегральных уравнений или неравенств, системы геометрических предложений или других математических объектов).

Анализ математической модели позволяет проникнуть в сущность изучаемых явлений. Математическая модель - мощный метод познания внешнего мира, а также прогнозирования и управления. Процесс математического моде­лирования, то есть изучения явления с помощью математических моделей, можно подразделить на четыре этапа.

С помощью метода математического моделирования раскрывается двойная связь математики с реальным миром. С одной стороны, математика служит практике по изучению и освоению объектов окружающего нас реального мира, с другой - сама жизнь, практика способствует дальнейшему развитию математики и направляет это развитие.

Метод математического моделирования состоит из нескольких этапов:

1. Поиск языка и средств для перевода задачи в математическую, т.е.

построение математической модели.

2. Изучение математической модели, ее исследование, расширение теоретических знаний учащихся.

3. Поиск решения математической задачи, рассмотрение различных способов решения, выбор наиболее рационального пути решения.

4. Перевод результата решения математической задачи в исходный, анализ модели в связи с накоплением данных об изучаемых явлениях и модернизация модели, а в будущем - построение новой, более совершенной математической модели.

Метод математического моделирования, сводящий исследование явлений внешнего мира к математическим задачам, занимает ведущее место среди других методов исследования. Методом математического моделирования решаются многие задачи межпредметного характера. Особенно актуальным это метод стал в связи с появлением ЭВМ.

Рассмотрим математические модели для обработки результатов эксперимента.

Валидность анкет (от лат. valid – пригодный) означает соответствие ее структуры и содержания показателей целям любой экспертизы. Для ее определения можно использовать коэффициенты ранговой корреляции и ввести ряд разновидностей как составляющих: – целеполагания (соответствия целям экспертизы); – конструкта (латентность); 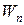– прогноза (результатов анкетирования); 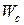– соответствия (другим методам исследования); – технологичность (сервисный характер).

Валидизацию анкет следует понимать как процедуру (методику, технологию) улучшения показателей валидности за счет увеличения знаний коэффициентов ее составляющих с использованием формулы:

(1)

где , , , , 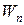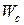– составляющие валидности, приведенные выше; 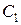… 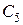– весовые коэффициенты важности разновидностей валидности.

Рассмотрим методику определения составляющих валидности. Валидность целеполагания анкеты, как и другие составляющие, для проведения педагогической экспертизы может быть определена по коэффициенту ассоциации Пирсона:

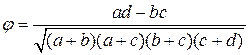
(2)

где значения входящих в формулу величин определяются из таблицы сопряженных признаков 2х2, содержащих частоты появления тех или иных событий. Стандартным видом такого рода информации является приведенная ниже таблица.

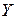
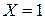
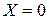
Единицы и нули в этой таблице символизируют в указанных условиях противоположные признаки: если оба признака и 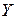присутствуют и достигают заданного значения ( и 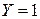), то их частота равна величине , если оба отсутствуют (или не достигают заданной величины), т.е. и 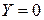, то величина равна частоте противоположных событий; величина соответствует числу событий, когда признак присутствует (), признак Y – нет (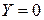); величина , когда наоборот.

Если 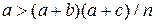, где – число значений признаков (оценок экспертов при экспертизе), то это свидетельствует о положительной корреляционной связи между признаками и 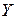(например, мнениями – суждениями двух групп экспертов).

Предположим, что две группы экспертов (разработчики анкеты и пользователи – признаки и 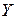) оценили пригодность анкеты, содержащей 6 вопросов, для цели экспертизы следующим образом:

№ вопроса							Среднее, балл	Среднее, %
, %
, %

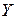В данной таблице приведены округленные до 10% средние значения ответов экспертов (в выборках и 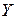) о пригодности каждого из 6 вопросов анкеты для цели экспертизы (оценка целеполагания анкеты). Анализируя приведенные значения, находим, что (для вопросов №1 и №4 средние оценки выше 85% в той и другой выборках); (для №2 и №3 в -выборке значения выше, чем в 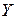-выборке); 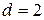(для №5 и №6 – они одновременно меньше 85%); . Вычисляя по формуле (2), получаем .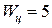

Предположим, что те же две группы экспертов (оценка валидности анкет должна проводиться в тех же выборках респондентов) оценили латентные возможности вопросов анкеты, т.е. их способность выявить поставленные вопросы, следующим образом:

№ вопроса							Среднее, балл	Среднее, %
, %
, %

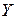Анализируя приведенные результаты, находим, что (№ 1, 2, 3, 4); 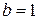(№ 5); 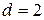(№ 6); 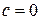. (Следует заметить, что 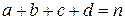, где – число объектов оценивания). Для получаем значение 0,6.

Валидность соответствия целесообразно определить между двумя вариантами анкеты, когда по-разному располагают в них вопросы (исследования на параллельность как в тестологии, когда тест делят на две части – для контрольной и экспертной групп), а также в тех случаях, когда сопоставляются авторские анкеты.

Функция как математическая модель реальных процессов

Математическая формула(от лат. formula – уменьшительное от forma – образ, вид) – принятая в математике (а также в прикладных науках) символическая запись законченного логического суждения (определения величины, уравнения, неравенства или тождества). В более широком смысле формула – всякая чисто символьная запись, противопоставляемая в математике различным выразительным способам, имеющим геометрическую иллюстрацию: чертежи, графики, диаграммы, графы и т.п.

Как правило, в формулу входят переменные (одна или более), причём сама формула представляет собой не просто выражение, а некое суждение. Такое суждение может утверждать что-то о переменных, а может — о применяемых операциях. Точный смысл формулы зачастую подразумевается из контекста и его невозможно понять непосредственно из её вида. Можно выделить три распространённых случая:

1. Формула должна сообщить, как искать значения переменной (уравнения и т.п.);

2. Формула (записываемая как «искомое = выражение») определяет величину через свои параметры;

3. Формула является собственно логическим утверждением: тождеством (например, аксиомой), утверждением теоремы и т.п.

Функция- зависимость переменной от переменной , если каждому значению соответствует единственное значение . Переменная – независимая переменная или аргумент. Переменная у- зависимая переменная.

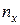Пусть известно статистическое распределение частот признака . Введем обозначения: – число наблюдений, при которых наблюдалось значение признак, меньшее ; – общее число наблюдений (объем выборки). Ясно, что относительная частота события 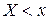равна 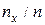. Если изменяется, то, вообще говоря, изменяется и относительная частота, т.е. относительная частота 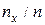есть функция от . Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической.

Эмпирической функцией распределения (функцией распределения выборки) называют функцию , определяющую для каждого значения относительную частоту события .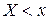

Итак, по определению, , где 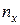– число вариант, меньших ; – объем выборки. Таким образом, для того чтобы найти, например, , надо число вариант, меньших , разделить на объем выборки: .

К математическим моделям педагогической экспертизы кроме расчетных соотношений для определения весовых коэффициентов показателей анкет и их валидности, приведенных выше, отнесем ряд моделей, аналогичных применяемым в тестологии. Это, прежде всего, логические модели, коэффициент надежности анкеты, погрешность результатов анкетирования, объем выборки анкетирования.

Естественно полагать, что результат экспертизы (или анкетного опроса) зависит в основном от двух факторов: валидности анкеты и компетентности эксперта (или подготовленности респондента). В общем случае результат экспертизы (анкетирования) имеет вероятностный характер и, следовательно, можно говорить о его количественном измерении некоторым числом p из отрезка . Таким образом, вероятность того, что определенный эксперт (респондент) ответит на вопросы анкеты, представляет собой некоторую функцию, по крайней мере, двух аргументов: 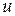– уровня подготовленности респондента (уровня компетентности эксперта) и 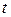– уровня трудности данного вопроса анкеты:

(3)

Коротко такую функцию будем называть функцией успешности анкетирования. Здесь 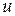и 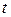– пока лишь просто символы, обозначающие определенные термины. Предположим, что в каком-нибудь смысле трудность некоторого вопроса анкеты в раз больше трудности другого вопроса, т.е.

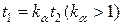
(4)

Трудность вопроса, прежде всего, зависит от его валидности (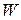), формулировки, компетентности эксперта, осведомленности респондента и ряда других факторов. Естественно, что в понятие «трудность вопроса анкеты» необходимо вкладывать смысл, при котором указанное соотношение (4) справедливо применительно к любому участнику анкетирования (эксперту, респонденту). Другими словами, первое задание (вопрос анкеты) должно оказаться в раз труднее для каждого анкетируемого (эксперта, респондента), а не только для какого-то конкретного человека.

Аналогичное положение должно иметь место и для понятия «уровень подготовленности». Если уровень подготовленности 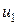в 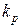раз выше (больше) уровня подготовленности 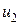другого анкетируемого, то это утверждение должно быть справедливым применительно к различным вопросам анкеты различной трудности ()

Пусть теперь

и , т.е.

(5)

Если допустить, что 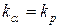, то вероятность ответа первым респондентом (экспертом), более подготовленным, на первое задание – вопрос (более трудное) должна совпадать с вероятностью ответа вторым респондентом, менее подготовленным, на второе задание (менее трудное).

Из приведенных рассуждений следует, что:

1) понятия 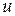и 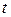тесно связаны между собой, и нельзя определить одно из них, не определив смысл другого;

2) функция (3) является однородной 1-го порядка, т.е. вероятность «успеха анкетирования» зависит, по существу, не от каждого аргумента 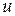и 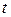персонально, а лишь от их отношения:

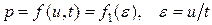
(6)

Переменные 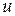и 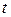принято называть латентными (ненаблюдаемыми) параметрами, поскольку они призваны описывать некоторые скрытые характеристики участников тестирования и анкет (валидность, надежность, погрешность). Для их количественного сопоставления среди многих респондентов и многих заданий (вопросов анкеты) необходимо определиться с единицами измерений. Для этой цели одному из вопросов анкеты можно приписать единичную трудность (например, определенное значение весового коэффициента или валидности), т.е. . В таком случае величина трудности любого другого к -го вопроса анкеты получает определенный смысл: этот к -й вопрос в раз труднее предыдущего () или легче (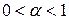), т.е. условие: 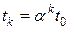. Зная значения весовых коэффициентов или валидности для отдельных вопросов анкеты, можно такое условие выполнить: , 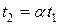и т.д. или , 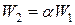и т.д.(видно, что 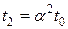или 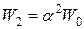и т.д.). Чтобы выполнить условие, аналогичное условиям композиции тестовых заданий в тесте (по возрастанию их трудности), необходимо и вопросы в анкете располагать в порядке возрастания значений их весовых коэффициентов (или уменьшения их валидности). Такое расположение вопросов в анкете позволит соотносить ответы на них: чем больше значение весового коэффициента (или меньше валидность) вопроса, тем менее вероятен на них ответ.

Аналогичные рассуждения справедливы и относительно уровней подготовленности u участников анкетирования (экспертизы). Область определения функций (6) – числовой промежуток [0; +∞), а множество их возможных значений есть отрезок [0;1]. На функцию такого типа естественно наложить следующие условия:

1) функция , где должна быть непрерывной вместе со своей производной и монотонно возрастающей на всей области своего определения, поскольку всякое увеличение отношения должно приводить к увеличению вероятности ответа на вопросы анкеты;

2) 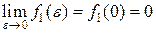, что делает маловероятным (безнадежным) ответы на вопросы анкеты абсолютно неподготовленного участника анкетирования (эксперта или респондента);

3) , что соответствует высокой вероятности ответов на анкету подготовленного респондента;

4) , т.е. максимальная неопределенность в предсказании ответа респондента на какой-то вопрос анкеты должна быть в том случае, когда уровень его подготовленности совпадает с трудностью вопроса, и она равна 0,5.

Вопросы для самоконтроля:

1. Понятие математической модели и математического моделирования.

2. Использование математического языка для записи и обработки информации.

3. Методы исследования как источник получения информации.

4. Математические и статистические методы.

5. Использование функции в теоретическом и эмпирическом исследовании.

Дата добавления: 2014-12-10