Потенциальное поле и его свойства

Упражнения

59. Доказать свойства ротора:

а) 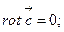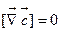, где 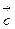=const

б)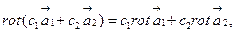

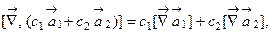где с₁, с₂ – постоянные коэффициенты.

в) 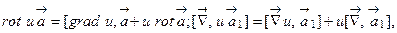где u - скалярное поле.

60. Вычислить ротор векторного поля:

а)

б)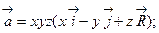

в)

61. Вычислить ротор векторного поля 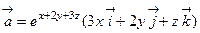в точке М₀ (3,-3,1).

62. Найти функцию векторного поля 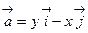вдоль замкнутой линии ABОA, где АВ – дуга астроиды, определяемой уравнением: 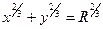или x=R cos³ t, y=R sin³ t.

Указание. Следует применить формулу Стокса:

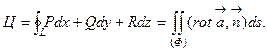
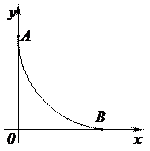Рис. 4.

3. С помощью формулы Стокса найти циркуляцию векторного поля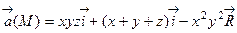

вдоль контура квадрата АВСDА определяемого уравнениями: – x+y=a; x+y=a; x–y=a; x+y=–a; z= 0.

64. Вычислить с помощью формулы Стокса циркуляцию векторного поля 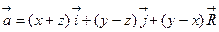вдоль окружностей:

а) (y+ 1 )² +(z– 1 )²= 1, x= 5 (вектор положительной нормали );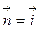

б) (x– 3 )² +(y– 2 )²= 4, z= 0 (вектор положительной нормали )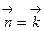

65. Доказать, что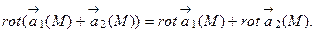

Векторное поле 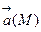называют потенциальным в области (G), если существует такая скалярная функция (скалярное поле) 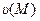, заданная в (G), что для всех точек этой области: 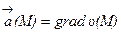. Функцию 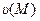называют потенциалом поля .

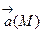В потенциальном поле линейный интеграл не зависит от формы пути и определятся только начальной и конечной точками пути, а именно

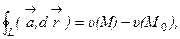
где М₀ и М – начальная и конечная точка линии (L).

Верно и обратное: если линейный интеграл поля 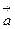(М) не зависит от пути, то поле 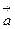(М) потенциально. Потенциал поля определяется с точностью до постоянного слагаемого. Это означает, что если 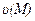один из потенциалов поля 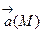, то выражения 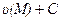при любом постоянном С также являются потенциалами поля. Задание величины потенциала в какой- либо точке М₀ области (V) однозначно определяет потенциал любой точки М:

, (*)

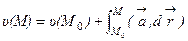где вместо 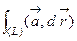использовано обозначение 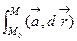, поскольку интеграл не зависит от пути.

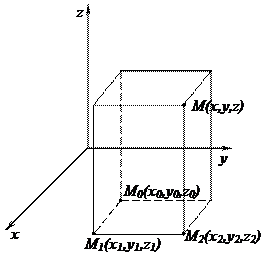Если поле задано в декартовой координатной форме: 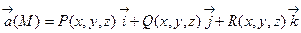, то для нахождения потенциала точки М(x,y,z) удобно взять линейный интеграл по ломанной М₀М₁М₂М _, звенья которой параллельны координатным осям.

Предполагается, конечно, что ломаная М₀М₁М₂М не выходит за пределы области (G). При таком выборе пути интегрирования и при дополнительном условии 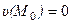выражение (*) принимает вид:

(*)

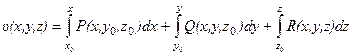При использовании этой формулы следует иметь в виду, что в каждом из трех входящих в нее интегралов одной буквой обозначают и верхний предел, и переменную интегрирования, т.е.

Рис. 5.

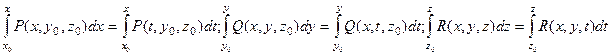
Отметим, что потенциальность поля 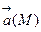и равенство нулю циркуляции поля по искомому простому кусочно-гладкому замкнутому контуру являются эквивалентными свойствами.

Если поле 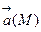потенциально в области (G), то в любой точке этой области 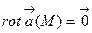. Это свойство потенциального поля является наиболее важным. Таким образом, потенциальное поле 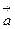(М) является безвихревым. Обратное, вообще говоря, неверно. Однако, если ограничиться поверхностно односвязными областями, то для таких областей понятие потенциального и безвихревого полей оказываются эквивалентными.

Дата добавления: 2014-12-10