Неопределенный интеграл. Функия называется первообразной для функции на промежутке Х, если в каждой точке х этого промежутка справедливо равенство

Функия 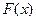называется первообразной для функции 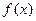на промежутке Х, если в каждой точке х этого промежутка справедливо равенство .

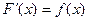Совокупность всех первообразных для функции 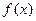на промежутке Х называется неопределенным интегралом от функции 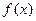и обозначается 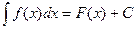, где С – произвольная постоянная. В записи 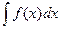функция 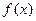называется подинтегральной функцией, а 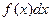- подинтегральным выражением. Нахождение неопределенного интеграла от некоторой функции называется интегрированием этой функции. Операции интегрирования и дифференцирования взаимно обратны.

Основные свойства неопределенного интеграла

1.

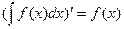
2.

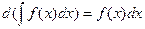
3.

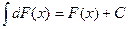
4. 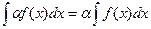, где - некоторое число

5.

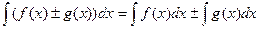
Табличные интегралы

1.

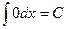
2. 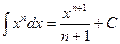, где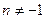

3.

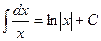
4. , где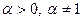

5.

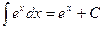
6.

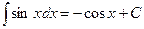
7.

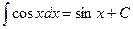
8. 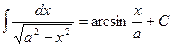, где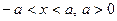

9.

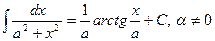
10.

11.

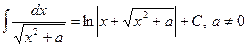
12.

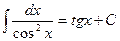
13.

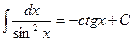
Методы интегрирования

Основное содержание различных методов нахождения интегралов состоит в сведении искомого интеграла к табличному или сумме интегралов. В простейших случаях это удается сделать, используя лишь эквивалентные преобразования подынтегральной функции и, если необходимо, свойства интегралов.

1. Метод замены переменной

Пусть 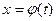- функция, непрерывно дифференцируемая на рассматриваемом промежутке. Тогда

.

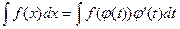Эта формула называется формулой замены переменной в неопределенном интеграле.

Пример 1. Найти интеграл .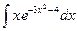

Решение. Сделаем замену 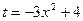, тогда , следовательно .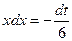

Тогда .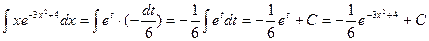

2. Метод интегрирования по частям

Пусть 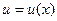и 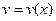- непрерывно дифференцируемые функции. Тогда справедлива формула:

.

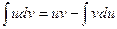Эта формула называется формулой интегрирования по частям.

Пример 2. Найти интеграл .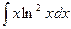

Решение. Пусть 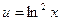, 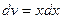. Тогда ,

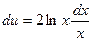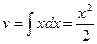
Применяя формулу интегрирования по частям, получаем

.

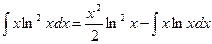Для нахождения последнего интеграла вновь применим формулу интегрирования по частям, сделаем замену 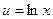, 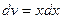. Тогда , .

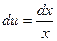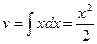Тогда .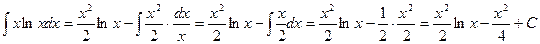

Следовательно, искомый интеграл равен

.

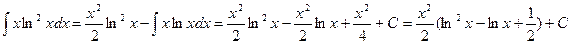3. Интегрирование рациональных выражений

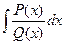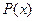Рассмотрим способы нахождения интегралов вида , где и 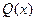- некоторые многочлены от переменной х.

Пусть знаменатель 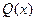допускает разложение на линейные множители:

,

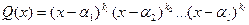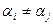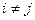где при и 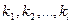- положительные целые числа. В этом случае дробь 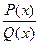допускает представление в виде суммы простейших дробей:

,

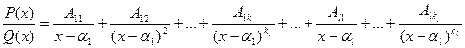где 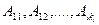- некоторые неизвестные числа. Поэтому рассматриваемый метод интегрирования называется методом неопределенных коэффициентов.

В случае, когда многочлен 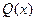не допускает разложения на линейные множители, в выражении дополнительно содержатся сомножители вида 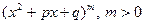, тогда разложение дроби 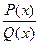дополнительно содержит слагаемые вида

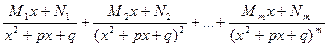
Пример 3. Найти интеграл .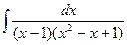

Решение. Разложим подинтегралную функцию на простейшие дроби:

.

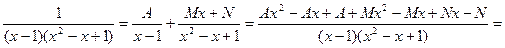
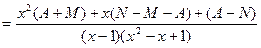Таким образом, 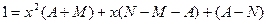, т.е.,

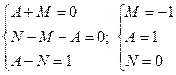
Разложение подынтегральной функции имеет вид:

.

.

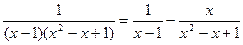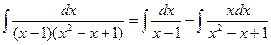Для первого интеграла преобразуем функцию под знаком дифференцила: 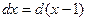, для второго – выделим полный квадрат в знаменателе 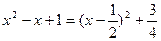и воспользуемся заменой переменной 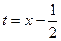, тогда .

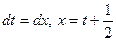Тогда,

.

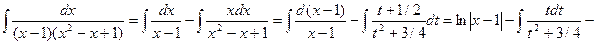
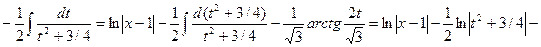
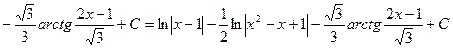Дата добавления: 2014-12-10