О вычислении интегралов от осциллирующих функций

Получение численных результатов решения осесимметричных, плоских и пространственных граничных задач для многослойных оснований связано с вычислением несобственных интегралов вида

(9.1)

где 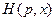– одна из функций . Лишь в отдельных случаях интегралы удается вычислить аналитическими методами. Поэтому в этом параграфе будут рассмотрены специальные численные методы для определения значений интегралов (9.1) при разных значениях параметра . Обычные приемы вычисления определенных интегралов, основанные на формулах средних, трапеций, Симпсона, Гаусса и других, при средних и больших значениях параметра могут давать недопустимо большую погрешность результатов вычислений.

Рассмотрим на простом примере, с какими трудностями приходится сталкиваться при вычислении на ЭВМ интегралов вида (9.1).

Пусть

. (9.2)

Функция 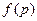является гладкой неотрицательной монотонно убывающей и интегрируемой в области . При таких предположениях относительно функции 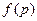интеграл (9.2) сходится равномерно относительно в области 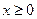(по признаку Вейерштрасса), так как функция 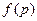является интегрируемой мажорантой для подынтегральной функции при любых значениях . На рис. (9.1) изображен условный график подынтегральной функции (9.2). Расстояние между соседними нулями функции равно , поэтому с ростом осцилляция подынтегральной функции усиливается.

Рисунок 9.1 ‑ График осциллирующей функции

Применение обычных способов вычисления интеграла (9.2) неэффективно при медленном стремлении к нулю функции 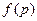с ростом и при больших значениях параметра осцилляции . Дело в том, что эти способы предназначены для вычисления площадей криволинейных трапеций, соответствующих задаваемым подынтегральным функциям. В случае осцилляции функций при больших значениях параметра осцилляции для приближенного вычисления определенного интеграла

,

близкого к рассматриваемому, нужно использовать очень большое число узлов выбранной квадратурной формулы, чтобы обеспечить хорошее приближение осциллирующей функции (между узлами) интерполяционными многочленами, на которых основана квадратурная формула. Это приводит к большому расходу машинного времени для вычисления интеграла. Вычисляемые при помощи квадратурной формулы площади для осциллирующей функции можно разбить на две последовательности, одна из которых состоит из положительных площадей (на рис. 9.1 эти площади помечены значком +), а другая – из отрицательных. При медленном убывании функции 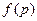или большом двум соседним площадям разного знака будут отвечать близкие по модулю их числовые значения. Поэтому сумма этих чисел, приближенно найденных при помощи ЭВМ, будет содержать меньше верных цифр, чем исходные слагаемые. Число верных цифр в вычислительной сумме будет уменьшаться с ростом . Еще меньше верных цифр может оказаться в окончательном результате вычисления интеграла (9.1.). Таким образом, применение обычных способов вычисления интегралов от осциллирующих подынтегральных функций с ростом параметра осцилляции приводит к увеличению расхода машинного времени ЭВМ и к сокращению числа верных цифр в полученном результате.

При вычислении несобственных интегралов (9.1) с заданной абсолютной погрешностью выбирают достаточно большое число , чтобы в правой части равенства

второе слагаемое по модулю не превосходило . Первое слагаемое при помощи специальных методов также вычисляют с погрешностью, не превышающей . Поэтому после отбрасывания второго слагаемого, приближенное вычисление несобственного интеграла (9.1) с погрешностью , сводится к вычислению определенного интеграла того же вида с погрешностью .

Для приближенного вычисления определенных интегралов с тригонометрическими ядрами осцилляции (интегралы Фурье)

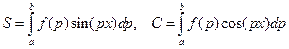(9.3)

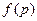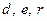целесообразно пользоваться методом Файлона [9]. Идея этого метода состоит в следующем. Промежуток интегрирования разбивается на достаточно большое число частей малой длины. На каждом промежутке функция аппроксимируется многочленом второй степени , коэффициенты в котором выбираются так, чтобы значения функции и многочлена точно совпадали в концах и середине отрезка . Используя вместо функции 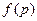аппроксимирующий ее многочлен и учитывая, что интегралы

можно вычислить точно для любых значений , в конечном итоге приходим к квадратурным формулам, позволяющим приближенно вычислять интегралы (9.3) как для малых, так и для больших значений параметра осцилляции . Абсолютная погрешность результата зависит от погрешности аппроксимации функции 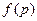многочленами на отрезках и не зависит от . Отсюда вытекает, что расход машинного времени ЭВМ при вычислении интегралов (9.3) с заданной абсолютной погрешностью будет одинаковым для любых . Опыт использования метода Файлона при решении граничных задач плоской теории упругости показывает, что с увеличением параметра осцилляции относительная погрешность результата (которая определяет число верхних цифр в нем) увеличивается, но значительно медленнее, чем при вычислении интегралов (9.3) обычными приближенными способами.

Приведем теперь квадратурные формулы Файлона для случая разбиения промежутка на одинаковых частей с длиной .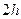

(9.4)

где

Чтобы избежать потери верных цифр при вычитании близких чисел, при для вычисления коэффициентов следует пользоваться разложениями их в ряды по степеням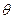

Приведем квадратурные формулы для приближенного вычисления интегралов Ханкеля

(9.5)

по значениям 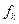функции 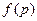в равностоящих узлах 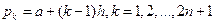. Предполагается, что .

Подробности построения квадратурных формул для интегралов и описаны в статье [10]. Метод их создания аналогичен методу Файлона и заключается в замене под знаком интеграла функции 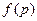на каждом промежутке близким квадратным трехчленом и точном вычислении интегралов

Квадратурные формулы для приближенного вычисления интегралов (9.5)имеют вид

(9.6)

где

Подробности вычисления значений функций можно найти в монографии [11] или в описаниях соответствующих подпрограмм для ЭВМ.

В заключение параграфа приведем формальное описание одного метода приближенного вычисления интегралов от осциллирующих функций (9,1), которым выгодно пользоваться для немалых по модулю значений параметра осцилляции .

Пусть

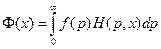
интеграл от осциллирующей функции с ядром 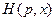, подлежащий вычислению. Рассмотрим вспомогательный интеграл

.

Подставляя в выражение для вместо 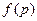степенной ряд , радиус сходимости которого предполагается бесконечным, получим

.

Рассмотрим функцию

.

Очевидно,

.

Поэтому

.

Переходя к пределу в этом равенстве при , получим разложение в ряд рассматриваемого интеграла

.

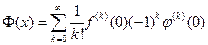Производные можно определить, разлагая функцию в ряд по степеням

,

где 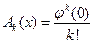. Подстановка 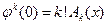в ряд для 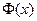приводит к окончательной формуле для вычисления интеграла

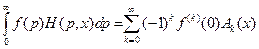. (9.7)

Подводя итог сказанному, приведем алгоритм построения формулы (9.7).

1. Вычислить при помощи таблиц [5,12] интеграл

.

2. Разложить вспомогательную функцию в ряд по степеням :

.

3. Воспользоваться коэффициентами для построения формулы (9.7).

В качестве примера построим формулу для вычисления интеграла

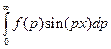
при больших значениях параметра осцилляции . В соответствии с алгоритмом находим функцию

.

Раскладываем в ряд по степеням

.

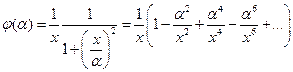Определяем коэффициенты

.

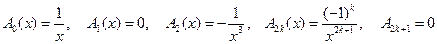В соответствии с (9.7) записываем искомую формулу

(9.8)

Вычислим при помощи этой формулы приближенное значение интеграла

.

Имеем

Удерживая три члена ряда в формуле (9.8), получаем

.

Точное значение интеграла равно 0,3.

Описанный способ можно применить ко всем рассмотренным в этом параграфе несобственным интегралам вида (9.1) с ядрами осцилляции Чем больше параметр осцилляции, тем меньше членов в ряде (9.7) нужно брать для приближенного вычисления интеграла с заданной абсолютной погрешностью.

Дата добавления: 2014-11-29