Модель задачи

Транспортная задача.

Задача линейного программирования.

Самыми простыми среди задач ИСО являются так называемые задачи линейного программирования. Для них характерно:

· целевая функция W линейно зависит от элементов решения х₁, х₂,..., х_n

· ограничения А, налагаемые на элементы решения, имеют вид линейных равенств или неравенств относительно элементов решения.

Такие задачи довольно часто встречаются на практике, например, при решении проблем, связанных с распределением ресурсов, планированием производства, организацией работы транспорта и т. д.

Для примера. Задача о пищевом рационе.

Ферма производит откорм скота. Для простоты допустим, что имеется всего четыре вида продуктов: П₁, П₂, П₃, П₄; стоимость единицы каждого продукта равна соответственно с₁, с₂, с₃, с₄. Из этих продуктов требуется составить пищевой рацион, который должен содержать: белков - не менее b₁ единиц; углеводов — не менее b₂ единиц; жиров — не менее b₃ единиц.

Таблица 3.

Про-	Элементы
дукты	белки	углеводы	жиры
П1	а11	а12	а13
П2	а21	а22	а23
П3	а31	а32	а33
П4	а41	а42	а43

Для продуктов П₁, П₂, П₃, П₄ содержание белков, углеводов и жиров a_ij (в единицах на единицу продукта) известно и задано в таблице.

Требуется составить такой пищевой рацион (т. е. назначить количества продуктов П₁, П₂, П₃, П₄, входящих в него), чтобы условия по белкам, углеводам и жирам были выполнены и при этом стоимость рациона была минимальна.

Составим математическую модель. Обозначим х₁, х₂, х₃, х₄ количества продуктов П₁, П₂, П₃, П₄, входящих в рацион. Целевую функцию требуется минимизировать. Она линейно зависит от элементов решения.

, или

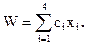
Итак, вид целевой функции известен и она линейна. Запишем теперь в виде формул ограничительные условия по белкам, углеводам и жирам. Учитывая, что в одной единице различных продуктов содержится различное количество ингредиентов a_ij, получим три неравенства.

Эти линейные неравенства представляют собой ограничения, накладываемые на элементы решения х₁, х₂, х₃, х₄.

Таким образом, поставленная задача сводится к следующей: найти такие неотрицательные значения переменных х₁, х₂, х₃, х₄, чтобы они удовлетворяли ограничениям — неравенствам и одновременно обращали в минимум линейную функцию этих переменных:

Это и есть математическая модель нашей задачи о рационе.

Классически, такие задачи решают симплексным методом.

Графическое решения задачи, на примере.

Концептуальная модель (постановка задачи). Кооператив выпускает два вида продукции – стекло и пенопласт. Трудозатраты на производство стекла – 20ч., пенопласта – 10ч. В кооперативе работают 10 рабочих по 40 ч. в неделю. Оборудование позволяет производить не более 15 т стекла и 20 т пенопласта в неделю. Прибыль от реализации 1 т стекла – 50 руб.; 1т пенопласта – 40 руб. Сколько материалов необходимо выпустить для получения максимальной прибыли?

50х₁+40х₂ max 20х₁+10х₂≤400 х₁≤15 х₂≤30 х₁≥0 х₂≥0  

Математическая модель.

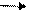На рисунке показано область допустимых решений рассматриваемой задачи. Она представляет собой совокупность точек, удовлетворяющих каждому ограничению.

Без доказательства: Если решение существует и единственное, то оно лежит в вершине области допустимых значений. Что бы получить оптимальное решение задачи, необходимо осуществить перебор вершин и выбрать ту, в которой целевая функция принимает максимальное значение.

Это положение лежит в основе симплекс-метода, позволяющего получить численное решение задачи линейного программирования.

В нашем примере оптимальным решением является вершина с координатами (5;30). W(5,30)=1450.

Оптимальное решение может быть не единственным. Тогда все точки какой либо прямой, ограничивающей область решений, соответствуют оптимальному решению.

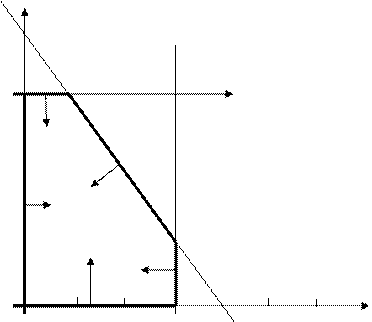40 х₂

5 10 15 20 25 30 х₁

Рис.10. Множество допустимых решений.

Транспортная задача – частный случай задачи линейного программирования. (Леонид Викторович Канторович)

В ТЗ существуют поставщики и потребители грузов. У каждого поставщика имеется определенное количество груза – мощность поставщика, а каждому потребителю нужно определенное количество груза – спрос потребителя. Известны затраты на перевозку единицы груза. Нужно составить такой план перевозок, при котором суммарные затраты на перевозку груза будут минимальными, по возможности будут задействованы все мощности поставщика и удовлетворен весь спрос потребителей.

Введем следующие переменные.

a_i – мощность поставщика (предложения продукта в пункте i=1,…,n), n – количество поставщиков.

b_j – спрос потребителя (в пункте j=1,…,m), m – количество потребителей.

c_ij - затраты на перевозку единицы продукции из пункта i в пункт j.

x_ij - количество груза, перевозимого из пункта i в пункт j.

В этих обозначениях транспортную задачу можно записать следующим образом.

Закрытая модель ТЗ (сбалансированная модель ТЗ) – модель, в которой суммарная мощность поставщиков равна суммарному спросу потребителей.

Общий спрос равен общему предложению (мощности всех поставщиков).

Открытая модель ТЗ (не сбалансированная модель ТЗ) – модель, в которой суммарная мощность поставщиков не равна суммарному спросу потребителей.

В процессе решения открытая модель всегда сводится к закрытой. Вводится фиктивный потребитель (что бы убрать неравенство) с недостающим спросом, но стоимость перевозок для него равна нулю (не меняет целевую функцию). Если суммарная мощность поставщиков меньше суммарного спроса потребителя, то вводится фиктивный поставщик, также получается закрытая модель, которая решаема.

Алгоритм решения закрытой модели ТЗ:

· Составляется специальная таблица поставщиков и потребителей с указанием их мощностей и спросов;

· Находим первоначальный план поставок:

- метод северо-западного угла;

- метод минимальной стоимости;

- метод потенциалов;

· Оптимизируем план распределительным методом;

Алгоритм рассмотрим на конкретном примере.

Имеется 4 поставщика А и 5 потребителей В. Мощности поставщиков и спрос потребителей, а также затраты на перевозку единицы груза для каждой пары поставщик-потребитель сведены в таблицу поставок:

Таблица 4.

ПОТ ПОСТ	В1	В2	В3	В4	В5	Мощность ai
А1
А2
А3
А4
Спрос bj

– искомый объем поставок i-го поставщика j-ому потребителю ().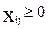

Запишем ограничения (уравнения баланса для каждой строки таблицы поставок):

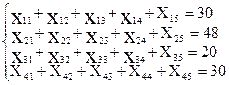
Уравнения баланса для каждого столбца таблицы поставок:

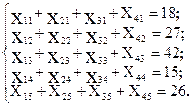
Целевая функция - суммарные затраты W на перевозку выражается через коэффициенты затрат

Будем называть любой план перевозок допустимым, если он удовлетворяет выше обозначенным условиям – все заявки удовлетворены, все запасы исчерпаны.

План (х_ij)будем называть оптимальным, если он, среди всех допустимых планов, приводит к минимальной суммарной стоимости перевозок W=min.

В силу особой структуры ТЗ (системы условий имеют единичные коэффициенты) при ее решении не приходится долго решать систему уравнений. Все операции по нахождению оптимального плана сводятся к манипуляциям непосредственно с таблицей, где в определенном порядке записаны условия транспортной задачи: перечень поставщиков и потребителей,спрос и мощности, а также стоимости перевозок.

Таблица 5

По мере заполнения этой таблицы в ее клетках проставляются сами перевозки х_ij Транспортная таблица состоит из т строк и п столбцов. В каждой клетке мы будем ставить стоимость перевозки единицы груза из А в В (правый верхний угол), а центр клетки оставим свободным, чтобы помещать в нее саму перевозку х _i,j. Клетку таблицы, соответствующую пунктам А и В будем кратко обозначать (i,j).

ПОТ ПОСТ	В1	В2	В3	В4	В5	Мощность ai
А1	18^13	12 ^7
А2		15 ^8	33 ^12	6
А3			9^10	11^8
А4				4^10	26^15
Спрос bj

Прежде всего займемся составлением допустимого плана. Это в транспортной задаче очень просто: можно, например, применить так называемый «метод северо-западного угла».

Начнем заполнение транспортной таблицы с левого верхнего («северо-западного») угла. Пункт В₁ подал заявку на 18 единиц груза; удовлетворим ее из запасов пункта А₁. После этого в нем остается еще 30 — 18 = 12 единиц груза; отдадим их пункту В₂. Но заявка этого пункта еще не удовлетворена; выделим недостающие 15 единиц из запасов пункта А₂ и т. д. Рассуждая точно таким же образом, заполним до конца перевозками х_ij транспортную таблицу (таблица 5).

Проверим, является ли этот план допустимым. Да, потому что в нем сумма перевозок по строке равна запасу соответствующего пункта отправления, а сумма перевозок по столбцу — заявке соответствующего пункта назначения (все заявки удовлетворены, все запасы израсходованы). Сумма запасов равна сумме заявок и выражается числом 128, стоящим в правом нижнем углу таблицы.

Проверим, является ли этот план допустимым. Да, потому что в нем сумма перевозок по строке равна запасу соответствующего пункта отправления, а сумма перевозок по столбцу — заявке соответствующего пункта назначения (все заявки удовлетворены, все запасы израсходованы). Сумма запасов равна сумме заявок и выражается числом 128, стоящим в правом нижнем углу таблицы.

Здесь и в дальнейшем мы проставляем в таблице только отличные от нуля перевозки, а клетки, соответствующие нулевым перевозкам, оставляем «свободными».

Проверим, можно ли таким планом пользоваться? Является ли система уравнений (ограничений – условий) совместной. Это из линейной алгебры. Число свободных клеток с нулевыми перевозками в таблице должно быть равно (т — 1)(п — 1) = 3х4 = 12. Если не так, то меняют угол, или меняют метод. При выполнении этого условия план называют опорным.

Теперь проверим план на оптимальность, т. е. минимальна ли для него общая стоимость перевозок? Скорее всего, нет (ведь составляя план, мы совсем не думали о стоимостях). Так и есть — план не оптимальный. Например, сразу видно, что можно его улучшить, если произвести в нем «циклическую перестановку» перевозок между клетками таблицы, уменьшив перевозки в «дорогой» клетке (2.3) со стоимостью 12, но зато увеличив перевозки в «дешевой» клетке (2.4) со стоимостью 6.

Например, перенесем 11 единиц груза по циклу (2.3) —>(2.4) —> (3.4) —> (2.3) —>(2,3). Чтобы план оставался опорным, мы должны заполнить одну из свободных клеток, а одну из занятых освободить. Сколько единиц груза можем мы перенести по циклу? Очевидно, не больше чем 11 единиц (иначе перевозки в клетке (3.4) стали бы отрица­тельными). В результате циклического переноса допустимый план остается допустимым — баланс запасов и заявок не нарушается.

Таблица 6

22 ^12	11^6
20^10	^8

Посмотрим, чего мы добились, сколько сэкономили.

Была стоимость: 33х12+11х8+9х10=574.

Стала стоимость: 22х12+11х6+20х10=530.

Мы уменьшили стоимость перевозок на 44 единицы. Это значение называется отрицательной ценой цикла. Общая стоимость плана составила W=1398

Оптимизация плана перевозок заключается в том, чтобы переносить («перебрасывать») перевозки по циклам, имеющим отрицательную цену.

В теории линейного программирования доказывается, что при опорном плане для каждой свободной клетки транспортной таблицы существует цикл, и притом единственный.

Таким образом, разыскивая в транспортной таблице свободные клетки (с отрицательной ценой цикла) и перебрасывая по циклу наибольшее возможное количество груза, мы будем все уменьшать стоимость перевозок. План, где не остается ни одной свободной клетки с отрицательной ценой цикла будет являться оптимальным.

Дата добавления: 2014-12-16