Предметом имитационного моделирования являются сложные системы, элементы и связи которых содержат множество случайных факторов

При имитационном моделировании не строится модель в виде системы уравнений относительно искомых величин.

В отличие от моделей исследования операций, которые должны быть сведены к целевой функции и ограничениям, имитационные модели имеют форму программно реализуемого алгоритма.

Суть имитационного подхода раскрывается в самом названии. Мы имитируем процесс функционирования системы во времени.

Отличительной чертой любой имитационной модели является структурное сходство с самой системой.

Проблема учета случайных факторов решается методом статистического моделирования. Наличие статистических данных является обязательным условием построения имитационных моделей.

По учету случайных факторов эти модели относятся к классу стохастических, то есть отражают случайный характер процессов.

Стохастичность - неизбежное свойство реальных сложных систем.

5.2. Оптимизация решения задач моделирования

Имитационная модель дает случайное значение результата моделирования (значения параметра, который необходимо оптимизировать). Оно называется реализацией модели. Но случайный результат не дает решение задачи. Применяется многократная реализация модели. В результате мы получаем множество случайных результатов (при заданном наборе исходных данных). Далее применяется аппарат математической статистики для обработки результатов моделирования. Можно получить усредненный результат, математическое ожидание его, рассчитать точность результата и т.п.

И так, моделируя систему и применяя метод метода статистического моделирования, мы можем имитировать множество значений исходных данных X, получить соответствующие множество выходных значений Y и с помощью статистических методов – получить вероятностные характеристики выхода.

Имитационные модели не включают в себя алгоритм поиска оптимального варианта решения. Но это не означает, что задача оптимизации не решается. Процесс оптимизации находится вне моделирующего алгоритма.

5.3. Метод Монте-Карло

Идея метода чрезвычайно проста и состоит в следующем. Вместо того чтобы описывать случайный процесс с помощью аналитического аппарата (дифференциальных или алгебраических уравнений), производится «розыгрыш» - моделирование случайного процесса с помощью специально организованной процедуры, дающей случайный результат.

Например. Построим модель процесса стрельбы спортсмена по мишени Мы знаем из опыта, что Р попадания его в цель составляет 0,8. Тогда, используя датчик (таблицу) случайных чисел на отрезке 0-1. Если выпадет число больше 0,8, то событие А (попадание) состоялось. Если меньше 0,8, то событие В(не попадание).

В действительности конкретная реализация случайного процесса складывается каждый раз по-иному. Мы получаем каждый раз новую, отличную от других реализацию исследуемого процесса.

Основным элементом, из совокупности которых складывается имитационная модель, является одна случайная реализация моделируемого явления, например: один «обстрел» цели», один «день работы» транспорта и т.п. Реализация представляет собой как бы один случай осуществления моделируемого случайного процесса со всеми присущими ему случайностями.

Сама по себе реализация ничего не дает.

(Например, мы же не можем делать выводы о качестве лекарства по одному случаю излечения).

Другое дело, если реализаций случайного процесса достаточно много. Это множество реализаций можно использовать как некий искусственно полученный статистический материал, который может быть обработан обычными методами математической статистики.

После такой обработки могут быть получены интересующие нас характеристики: вероятности событий, математические ожидания и дисперсии случайных величин и т. д.

При моделировании случайных процессов методом Монте-Карло сама случайность используется как аппарат исследования.

Для построения моделей методом Монте-Карло необходимо знать вероятностные характеристики случайных факторов, необходимо иметь статистику процессов.

М етодом Монте-Карло может быть решена любая вероятностная задача. Но метод используется только тогда, когда процедура розыгрыша проще, а не сложнее аналитического расчета.

Приведем пример, когда метод Монте-Карло возможен, но крайне неразумен.

Пример 1. Пусть спортсмен производит несколько независимых выстрелов по мишени. Каждый выстрел попадает в мишень (событие А) с одинаковой вероятностью Р(А). Требуется найти вероятность хотя бы одного попадания.

Аналитический способ. Модель процесса попадания в мишень хотя бы одним выстрелом можно представить в следующем виде

Р=1 - (1-Р(А))ⁿ.

Рассмотрим частный случай, когда Р(А)=0,5, а количество выстрелов равно 3. Тогда

Р=1- 0,5³= 7/8.

Розыгрыш. Ту же задачу можно решить и «розыгрышем», статистическим (имитационным) моделированием. Будем бросать «три монеты», считая, скажем, орел — за «попадание», решку — за «промах». Опыт считается «удачным», если хотя бы на одной из монет выпадет герб. Произведем очень много опытов, подсчитаем общее количество «удач» и разделим на число N произведенных опытов. Таким образом, мы получим частоту события, а она при большом числе опытов близка к вероятности.

Использование такого приема возможно, но неоправданно трудоемко.

Пример 2. Задача о «случайном блуждании». Прохожий решил прогуляться, стоя на углу пересечения улиц. Пусть вероятность того, что, достигнув очередного перекрестка, он пойдет на север, юг, восток и запад, одинакова. Какова вероятность того, что пройдя 10 кварталов, прохожий окажется не далее 2 кварталов от места, где он начал прогулку.

Количество исходов на каждом перекрестке равно 4. Тогда общее количество исходов равно 4¹⁰. (Такая задача похожа на шахматную. Сколько будет зерен на последней клетке, если на первую положить одно и удваивать число по мере продвижения по клеткам?).

Эту задачу модно решить только имитацией – розыгрышем. Другими методами такую задачу решить практически невозможно.

Обозначим его местонахождение на каждом перекрестке двумерным вектором (x₁, x₂) («выход»), где x₁ – направление с востока на запад и x₂ – направление с севера на юг. Каждое перемещение на один квартал к востоку (x₁ + 1), а каждое перемещение на один квартал к западу (x₁ – 1) (x₁ - дискретная переменная). К северу x₂ + 1, к югу x₂ – 1. Начальное положение (0,0).

Если в конце прогулки абсолютные значения х₁ и х₂ будут больше 2, то будем считать, что он ушел дальше двух кварталов в конце прогулки протяженностью в 10 кварталов. Т.к. вероятность движения нашего прохожего в любом из 4 направлений по условию одинакова и равна 0,25, то можно оценить его передвижение с помощью таблицы случайных чисел. Условимся, что если случайное число (СЧ) лежит в пределах от 0 до 24, прохожий пойдет на восток и мы увеличим х₁ на 1; если от 25 до 49, то он пойдет на запад и х₁-1; если от 50 до 74, он пойдет на север и x₂ + 1; если от 75 до 99, то на юг и x₂ – 1.

Нужно провести достаточно большое число «машинных опытов», чтобы получить достоверный результат.

Метод имитационного моделирования может рассматриваться как своеобразный экспериментальный метод. Отличие от обычного эксперимента заключается в том, что в качестве объекта экспериментирования выступает имитационная модель, реализованная в виде программы на ЭВМ или в виде некоторого игрового эксперимента. При таком экспериментировании с моделью для получения количественных оценок (например, математическое ожидание исследуемого параметра) применяются статистические методы.

Методом статистических испытаний можно находить не только вероятности событий, но и средние значения (математические ожидания) случайных величин. При этом применяется закон больших чисел (теорема Чебышева ). Согласно этой теореме, при большом числе опытов среднее арифметическое наблюденных значений случайной величины почти наверняка мало отличается от её математического ожидания. Аналогичным образом могут быть найдены не только математические ожидания, но и дисперсии интересующих нас случайных величин.

В качестве математических схем, используемых для моделирования случайных факторов, используются схемы случайных событий, случайных величин и случайных процессов (функций). Все они сводятся к выработке и преобразованию случайных чисел.

В качестве исходной совокупности случайных чисел обычно исполь­зуют совокупность случайных чисел R с равномерным распределением в интервале [0,1]. При машинном моделировании используется датчик случайных чисел.

5.4. Основные свойства равномерного распределения случайных величин.

· Плотность распределения f(х), где х – случайная величина, постоянна на отрезке (a, b) и равна нулю вне этого отрезка (Ошибка! Источник ссылки не найден. 3).

Рис. 19 Плотность распределения и функция распределения равномерно распределенной случайной величины на интервале (а,в)

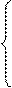c, если а ≤ х ≤в;

f(x) =

0, если х <а или х > в,

Так как площадь, ограниченная кривой плотности, равна единице, то

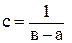для а ≤ х ≤ в.

· Функция распределения F(х) выражается площадью под кривой плотности f(x), лежащей левее точки X и, следовательно,

0, если х < а,

F(x) = (х-а)/(в-а), если а ≤ х ≤ в;

1, если х > в.

· Математическое ожидание равномерно распределенной случайной величины

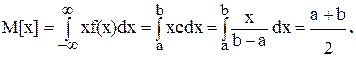
· Дисперсия случайной величины, распределенной равномерно

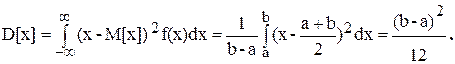
Случайные числа служат исходным материалом для моделирования случайных событий, случайных величин и случайных процессов. Для такого моделирования необходимо знать вероятности событий и случайных величин.

5.5. Моделирование случайных событий

Под случайным событием в теории вероятности понимается всякий факт, который в результате опыта может произойти или не произойти. Например, спортивная стрельба по летящим тарелочкам. Событие А – попадание (тарелочка поражена), событие Ā – промах, вероятность попадания - Р(А). Различные виды случайных событий имеют различные алгоритмы моделирования.

5.5.1. Моделирование одиночного случайного события

Пусть нам необходимо смоделировать некоторое событие А с известной его вероятностью появления Р(А). Алгоритм моделирования

заключается в следующем:

· Выбирается случайное число R, подчиненное закону равной вероятности на отрезке [0,1] (при обращении к датчику случайных чисел)

· Случайное число сравнивается с вероятностью появления события.

Если вероятность больше числа, то событие произошло.

Если вероятность меньше числа, то событие не произошло.

То есть

Следует помнить, что количество знаков после запятой в случайном числе должно быть не менее, чем в вероятности события А.

Продолжим пример со спортивной стрельбой. Построим модель поражения летящей мишени. Определим событие А, как поражение цели. Это событие случайное. Оно зависит от многих случайных факторов: порыв ветра, вес патрона, состояние стрелка в момент выстрела и т.п.

По результатам стрельбы имеем статистику – результативность стрелка. Пусть, например, из 100 выстрелов он попадает, как правило, 80 раз. Отсюда следует, что вероятность события А (успешного выстрела для данного стрелка) равна Р(А) = 0,8.

Тогда моделирование процесса будет выглядеть следующим образом:

· Выбираем случайное число R. Датчики случайных чисел могут выдавать набор чисел в различных диапазонах, например – [0,1] или [00,99] и т.п. Если диапазон случайных чисел не совпадает с диапазоном изменения вероятности, необходимо привести их к одному диапазону.

· Пусть R=75. Нормируем случайное число, приводя его к случайному диапазону R`=R / 100 = 0,75.

· Сравниваем два числа. Р(А) > R`, значит стрелок попал в цель.

Такую модель на компьютере построить очень просто.

Блок-схема алгоритма моделирования может быть представлена следующим образом.

Необходимо обратить внимание, что в построенной выше модели, мы не писали аналитические уравнения полета пули, поражения мишени и т.п. Мы построили имитационную модель, непосредственно имитируя сам процесс. В этом смысле, метод Монте-Карло называют экспериментом на бумаге.

Если нам необходимо построить модель сложного производственного процесса, который представляется последовательностью случайных событий. В этом случае, построив модель каждого события, мы тем самым построим модель всего процесса.

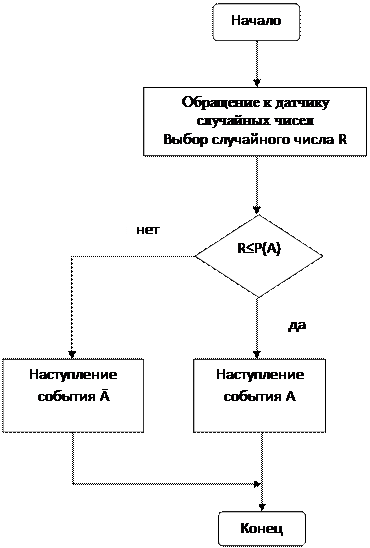Рисунок 20 Алгоритм моделирования случайного события

5.5.2. Моделирование двух независимых случайных событий

Два события называются независимыми, если факт наступления одного из них не зависит от наступления другого события.

Пусть два независимых случайных события А и В наступают с известными вероятностями Р(А) и Р(В) соответственно. (Как мы ранее говорили – для моделирования стохастических событий – нужны их вероятности). Возможными исходами совместных испытаний могут быть четыре события (Таблица 1)

Таблица 10

События	Исходы
А	+	+	-	-
В	+	-	+	-

Моделирование исхода испытаний заключается в последовательном моделировании наступлений событий А и В. Следует иметь в виду, что для моделирования наступления каждого события выбирается свое случайное число R (используется отдельный датчик случайных чисел).

Естественно, можно рассматривать и несколько событий – только больше будет исходов.

Примеры независимых событий - выступление команды стрелков, бросание нескольких игральных костей.

Алгоритм моделирования следующий:

· Определяем случайное число R_1.

· Сравниваем R₁ с Р(А) и получаем исход (+), если Р(А) > R₁ или (-), если меньше).

· Определяем случайное число R_2.

· Если на шаге 2 исход был (+), т.е. событие А состоялось, то сравниваем R₂ ~ Р (В) и получаем исходы (+) или (-).

Если на шаге 2 исход был (-), т.е. состоялось событие Ā. Сравниваем R₂ ~ Р (В) и также получаем исходы (+) или (-).

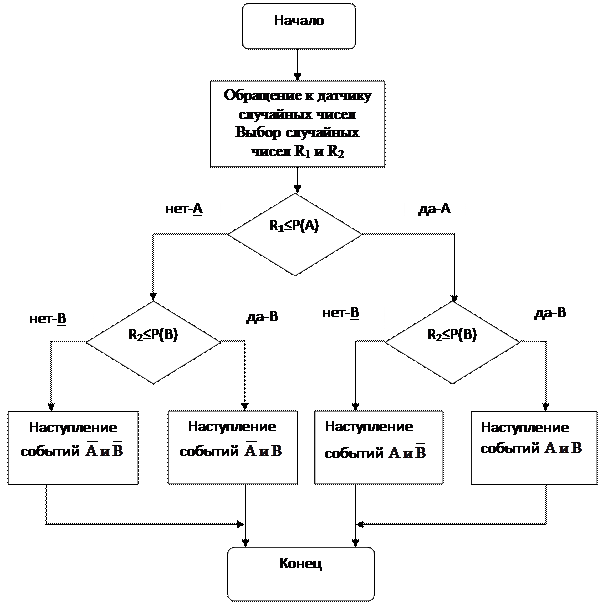Рисунок 21 Алгоритм моделирования двух независимых случайных событий

5.5.3. Моделирование двух зависимых случайных событий

Пусть два зависимых случайных события А и В имеют вероятности соответственно Р(А) и Р(В).

Что означает зависимость событий?

Для зависимых случайных событий существуют условные вероятности. Будем считать их заданными:

Р_А(В) – вероятность появления события В при условии появления события А.

Р_Ā(В) – вероятность появления события В при не появлении события А.

Как и в предыдущем примере имеем четыре исхода.

Таблица 11

События	Исходы
А	+	+	-	-
В	+	-	+	-

В качестве исходных данных необходимо знать, по крайней мере, три вероятности. Если неизвестна одна из условных вероятностей, например Р_Ā(В), то ее можно определить из формулы полной вероятности

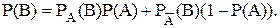
Процесс моделирования будет содержать четыре шага:

· Определяем случайное число R_1.

· Сравниваем R₁ с Р(А) и получаем исход (+), если Р(А) > R₁ или (-), если меньше).

· Определяем случайное число R_2.

· Если на шаге 2 исход был (+), т.е. событие А состоялось, то сравниваем R₂ ~ Р _А(В) и получаем исходы (+) или (-).

Если на шаге 2 исход был (-), т.е. состоялось событие Ā, то сравниваем R₂ ~ Р _Ā (В) и также получаем исходы (+) или (-).

Блок-схема моделирования идентична предыдущей за исключением сравнения с R₂ - необходимо заменить Р(В) на Р_А (В) и Р _Ā (В) в соответствующих блоках.

Рис. 22 Алгоритм моделирования двух зависимых случайных событий

5.5.4. Моделирования случайного события из полной группы событий

Полной группой событий называется несколько событий таких, что в результате опыта непременно должно произойти хотя бы одно из них. События, составляющие полную группу являются взаимоисключающими. Например, стрельба по мишени. Событие А₀ – попадание в молоко, событие А₁ - попадание в 1 и т.д. Или игральные кости: хотя бы одно число выпадает и числа взаимоисключающие.

Для моделирования случайного события из полной группы в качестве исходных данных должен быть задан ряд распределения вероятностей этих событий Р_i. Пусть мы имеем n событий А₁, А₂... А_n, составляющих полную группу. И задан ряд распределения вероятностей этих событий, то есть P₁, P₂, P_n. Из определения полной группы следует:

.

Это условие говорит о том, совокупность всех событий А_i такова, что одно из них обязательно должно произойти (монета упадет либо на «орел» либо на «решка») и произойти может только одно событие.

Пусть мы имеем n событий А₁, А₂,... А_n, составляющих полную группу. И задан ряд распределения вероятностей этих событий, то есть Р_i, причем . По заданному ряду распределения формируется интервальная шкала. Она представляет последовательность отрезков, расположенных на интервале [0,1]. Протяженность отрезков пропорциональна соответствующим вероятностям.

Вероятность, указанная на интервальной шкале называется кумулятивной, или интегральной вероятностью.

Рис. 23 Интервальная шкала

При построении шкалы не имеет значения, в какой последовательности указаны события, они независимые. Отсечка на шкале соответствует сумме вероятностей событий слева от отсечки.

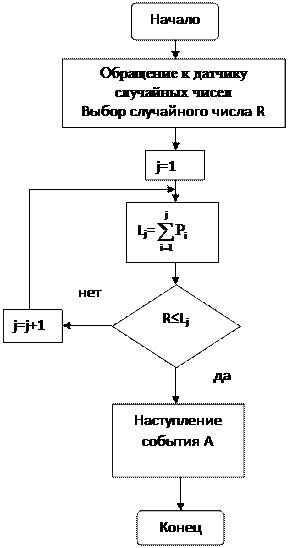
Запуск счетчика

Рисунок 24 Алгоритм жеребьевки

Процесс моделирования сводится к следующему. Выбираем случайное число R. Определяем интервал, на который попало случайное число.

Считаем, что произошло событие А_i, соответствующее данному интервалу.

Процедуры, построенные в соответствии с данным алгоритмом, называются жеребьевкой (Рисунок 7).

В качестве примера алгоритма жеребьевки построим модель игральной кости.. Имеем шесть событий: А₁ – выпала 1, А₂ – выпала 2 и т.д.

Из опыта знаем, что Р₂ = Р₂ =... 0,1(6). Изобразим интервальную шкалу (Рис8).

Рис. 25 Интервальная шкала для модели подбрасывания монеты

Модель представляется в виде таблицы.

Таблица 12

Событие	Кумулятивная вероятность с точностью до второго знака	Интервал случайных чисел
А1	0,1(6) -0,17	0 – 0,16
А2	0,(3) – 0,33	0,17 – 0,32
А3	0,5	0,33-0,49
А4	0,6(6)-0,67	0,5-0,66
А5	0,8(3)-083	0,67-0,82
А6		0,83-0,99

Выбираем случайное число, например R=0,71. Определяем, в какой интервал попало случайное число. В данном случае произошло событие А₅ –выпала пятерка.

5.6. Моделирование случайных величин

Случайной величиной называется величина, которая в результате опыта может принять то или иное значение (неизвестное заранее).

Например, количество изделий выпускаемых заводом в смену.

Случайные величины бывают дискретными и непрерывными.

Дискретные – такие, отдельные значения которых можно заранее перечислить. Например, рост взрослого человека в сантиметрах. (Не надо путать дискретную случайную величину со случайным событием. Напомним, что под случайным событием в теории вероятности понимается всякий факт, который в результате опыта может произойти или не произойти.).

Непрерывные величины образуют сплошное заполнение некоторого промежутка числовой оси.

Например, скорость бега спортсмена.

В соответствии с этим и модели делятся на дискретные и непрерывные.

5.6.1. Моделирование дискретной случайной величины

Дискретная случайная величина А, принимающая конечное число возможных значений, задается перечнем этих значений А₁,.А₂,...А_n и вероятностями того, что случайная величина примет каждое из них Р₁, Р_2,…Р_n. Случайная величина может принять только одно значение из множества возможных. При этом события, заключающиеся в том, что А примет значения А₁,.А₂,...А_n, образуют полную группу. Поэтому, моделирование значений дискретной величины А осуществляется алгоритмом жеребьевки (Моделирования случайного события из полной группы событий).

Пример построения модели.

Будем моделировать поток машин на автомойку в течение 10 часов.

Для моделирования необходимо знать вероятностные характеристики потока машин. Имеем статистику количества машин, приезжавших на мойку в течении последних 200 часов (имитационную модель можно построить только на основе статистических данных).

Таблица 13

Число машин в час.	Частота

Составляем интервальную шкалу.

Таблица 14

Число машин в час	Частота	Вероятность	Кумулятивная вероятность*[1]	Интервал случайных чисел
		0,10	0,10	0 – 0,09
		0,15	0,25	0,1-0,24
		0,25	0,50	0,25-0,49
		0,30	0,80	0,50-0,79
		0,20		0,80-0,99
Сумма

Диапазон случайных чисел устанавливаем в соответствии с кумулятивной вероятностью, как показано в таблице. Полученная таблица используется следующим образом. С помощью датчика определяем 10 случайных чисел. Определяем, в какой интервал нашей таблицы они попадают и находим соответствующее значение прибытия машин. Имитационная модель будет представлять собой следующую таблицу.

Таблица 15

Час
Случайное число	0,69	0,02	0,36	0,49	0,71	0,99	0,32	0,10	0,75	0,21
Количество прибывших машин

Получаем, что за 10 часов подъедет на мойку 61 машина. В среднем это составит 6 машин в час. Эти данные позволяют на практике оценить необходимую производительность мойки по имеющейся статистики потока машин. Можно подсчитать математическое ожидание этой случайной величины. Оно будет отличаться от среднего значения, но с ростом числа испытаний эта разница уменьшается.

Дата добавления: 2014-12-16