Проекции скорости и ускорения

v = v₀cos( ωt+φ₀) и a_x = -a₀sin ( ωt+φ₀)

v₀ = A ω - амплитуда скорости

a₀ = A ω² = v₀ ω - амплитуда ускорения

Кинетическая энергия материальной точки, совершающей прямолинейные гармонические колебания равна

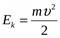
Потенциальная энергия материальной точки, гармонически колеблющейся под действием квазиупругой силы, равна

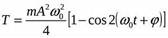
Колебания потенциальной и кинетической энергии совершаются со сдвигом по фазе на π, так что полная механическая энергия материальной точки не изменяется при колебаниях.

Математический маятник - материальная точка, точка подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости под действием силы тяжести. Математический маятник представляет собой предельный случай физического маятника, вся масса которого сосредоточена в его центре масс.

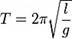
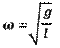
Период Циклическая частота

l - длина математического маятника.

g - ускорение свободного падения.

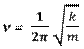Пружинный маятник - материальная точка массы m, совершающая прямолинейные гармонические колебания под действием упругой силы. Груз массы m, подвешенный на абсолютно упругой пружине.

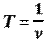
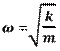
Циклическая частота Частота колебаний Период

k - жесткость пружины.

m - масса груза.

Физический маятник - твердое тело, имеющее возможность качаться под действием его силы тяжести вокруг неподвижной горизонтальной оси, не проходящей через центр тяжести тела.

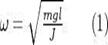
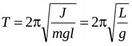
Период Циклическая частота

J - момент инерции маятника, относительно оси.

L - приведенная длина физического маятника - условная характеристика физического маятника. Численно равна длине математического маятника, период которого равен периоду данного физического маятника.

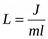
Приведенная длина физического маятника

Под сложением колебаний понимают нахождение закона результирующих колебаний системы в тех случаях, когда эта система одновременно участвует в нескольких колебательных процессах.

Различают два предельных случая:

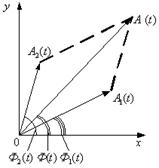Сложение колебаний одинакового направления

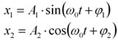Используя метод вращающегося вектора амплитуды, сложим гармонические колебания одного направления и одинаковой частоты

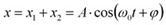Уравнение результирующего колебания имеет вид

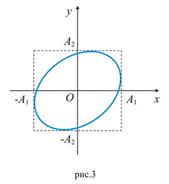
Амплитуда результирующего колебания при этом равна

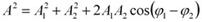
Амплитуда А результирующего колебания зависит от разности фаз (φ ₁ - φ ₂) складываемых колебаний.

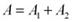если (φ ₁ - φ ₂) = ± 2mπ (m = 0, 1, 2, 3,...), то амплитуда результирующего колебания равна сумме амплитуд складываемых колебаний

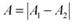если (φ ₁ - φ ₂) = ± (2 m +1) π (m = 0, 1, 2, 3,...), то амплитуда результирующего колебания равна разности амплитуд складываемых колебаний

Начальная фаза результирующего колебания находится по формуле

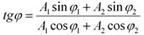
Cложение взаимноперпендикулярных колебаний

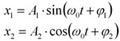Пусть точка М одновременно колеблется вдоль осей координат ОХ и ОУ по законам

где х и у - декартовы координаты точки М.

Уравнение траектории результирующего движения точки М в плоскости ХОУ можно найти, исключив из выражений для х и у параметр t

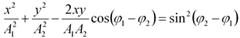
Фигуры Лиссажу - замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях.

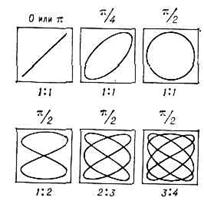
Вид фигур Лиссажу при различных соотношениях периодов (1:1, 1:2 и т. д.) и разностях фаз.

Фигуры Лиссажу получаются при сложении двух взаимно перпендикулярных колебаний. Они могут быть довольно сложными, особенно при близких частотах продольных и поперечных колебаний.

Вид Лиссажу фигуры зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний.

Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат.

Фигуры Лиссажу можно наблюдать на экране осциллографа; они получаются в результате перемещения светящейся точки, если к двум парам отклоняющих пластин подведены переменные напряжения с равными или кратными периодами.

Затуханием колебаний называется постепенное ослабление колебаний с течением времени, обусловленное потерей энергии колебательной системой. Свободные колебания реальных систем всегда затухают.

Затухание свободных механических колебаний вызывается трением и возбуждением в окружающей среде упругих волн. Затухание в электрических колебательных системах вызывается тепловыми потерями в проводниках, диэлектриках и ферромагнетиках.

Закон затухания колебаний зависит от свойств колебательной системы.

Свободные затухающие колебания линейной системы. Система называется линейной, если параметры, характеризующие физические свойства системы, не изменяются в ходе процесса.

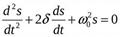
Дифференциальное уравнение свободных затухающих колебаний линейной системы

s, х, q - изменяющаяся при колебаниях физическая характеристика системы.

β - const > 0, коэффициент затухания.

ω₀ - циклическая частота свободных незатухающих колебаний.

Свободные затухающие колебания пружинного маятника. На маятник массы m, совершающий прямолинейные колебания вдоль оси ОХ под влиянием силы упругости пружины, действует также сила сопротивления.

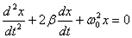
Дифференциальное уравнение свободных затухающих колебаний маятника

Дата добавления: 2014-12-16