
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод Гаусса. Системе m линейных уравнений (1)
|
|
|
|
Системе m линейных уравнений

| (1) |
можно поставить в соответствие расширенную матрицу:
 . .
| (2) |
Существует взаимно-однозначное соответствие между элементарными преобразованиями линейной системы и операциями над строками расширенной матрицы.
Действительно,
- Перестановка уравнений системы соответствует перестановке строк расширенной матрицы.
- Умножение уравнения на ненулевое число соответствует умножению строки на это число.
- Сложение уравнений системы соответствует сложению строк матрицы.
Решение системы (1) методом Гаусса представляет собой не что иное как преобразование расширенной матрицы к треугольному или ступенчатому виду:
 , ,
| (3) |
где опущены строки, состоящие из нулевых элементов.
Матрица такого вида соответствует более простой системе уравнений, решение которой начинается с решения последнего уравнения, затем результат подставляется в предпоследнее уравнение и т.д.
Если число неизвестных превышает число уравнений, то часть неизвестных (n-r) рассматривается в качестве свободных параметров и называются свободными переменными. Остальные r переменных выражаются через свободные и называются опорными, базовыми, определёнными, зависимыми.
Формально схема преобразований расширенной матрицы выглядит следующим образом.
- Предположим, что матричный элемент a 11 первого столбца матрицы (2) отличен от нуля. (В противном случае достаточно предварительно переставить местами первую строку этой матрицы с какой-нибудь другой.)
Для получения нулей в первом столбце матрицы (2) достаточно прибавить ко второй строке этой матрицы первую, умноженную на (- a 11/ a 12), к третьей строке - первую, умноженную на (- a 11/ a 13) и так далее.
В результате первый столбец содержит единственный отличный от нуля элемент a 11. - Затем воспроизводим алгоритм, изложенный на предыдущем этапе, применительно ко второму столбцу полученной матрицы.
Предположим, что матричный элемент a 22 второго столбца этой матрицы отличен от нуля. (В противном случае достаточно предварительно переставить местами соответствующую строку матрицы с какой-нибудь другой нижележащей.)
Для получения нулей во втором столбце рассматриваемой матрицы достаточно прибавить к третьей строке матрицы вторую, умноженную на (- a 22/ a 23), к третьей строке - первую, умноженную на (- a 22/ a 24) и так далее.
В результате второй столбец содержит единственный отличный от нуля элемент a 22. - И так далее.
- В конечном итоге мы получаем матhицу вида (3).
Примеры:
|
|
|
1. Решить систему уравнений
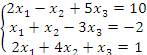 методом Гаусса. Решение. Рассмотрим расширенную матрицу и приведем ее к треугольному виду, выполняя операции над строками:
методом Гаусса. Решение. Рассмотрим расширенную матрицу и приведем ее к треугольному виду, выполняя операции над строками:
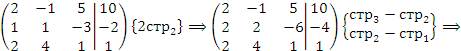 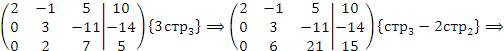  Полученная матрица описывает систему уравнений
Полученная матрица описывает систему уравнений
 эквивалентную исходной системе. Решение находится элементарно:
эквивалентную исходной системе. Решение находится элементарно:
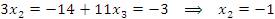 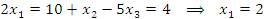 Убедимся в том, что полученный набор
Убедимся в том, что полученный набор  обращает каждое уравнение данной системы в тождество: обращает каждое уравнение данной системы в тождество:

|
***
2. Решить систему уравнений
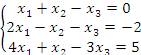 методом Гаусса. Решение. Преобразуем расширенную матрицу, производя элементарные операции над строками:
методом Гаусса. Решение. Преобразуем расширенную матрицу, производя элементарные операции над строками:
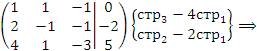 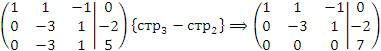 Третья строка этой матрицы соответствует уравнению
Третья строка этой матрицы соответствует уравнению
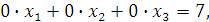 не имеющему решений и, следовательно, система является несовместной.
не имеющему решений и, следовательно, система является несовместной.
|
***
3. Решить систему уравнений
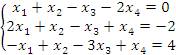 методом Гаусса. Решение. Производя элементарные преобразования над строками, приведем расширенную матрицу к ступенчатой форме:
методом Гаусса. Решение. Производя элементарные преобразования над строками, приведем расширенную матрицу к ступенчатой форме:
 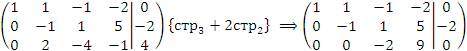 Выпишем соответствующую систему уравнений:
Выпишем соответствующую систему уравнений:
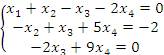 Последнее уравнение содержит две переменных, одну из которых нужно рассматривать в качестве свободного параметра. Назначим этому параметру произвольное значение
Последнее уравнение содержит две переменных, одну из которых нужно рассматривать в качестве свободного параметра. Назначим этому параметру произвольное значение 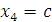 и выразим остальные переменные через c: и выразим остальные переменные через c:
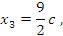  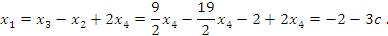 Таким образом, общее решение системы имеет вид
Таким образом, общее решение системы имеет вид
 Если подставить вместо c произвольное число, например нуль, то мы получим частное решение:
Если подставить вместо c произвольное число, например нуль, то мы получим частное решение: 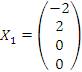 .
Подставляя c = 2, получаем другое частное решение: .
Подставляя c = 2, получаем другое частное решение: 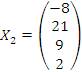 .
Таким образом, данная система имеет бесконечное множество решений. Проверка: Подставим .
Таким образом, данная система имеет бесконечное множество решений. Проверка: Подставим 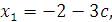   и и 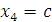 в каждое уравнение системы: в каждое уравнение системы:
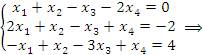 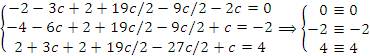 Уравнения обратились в тождества.
Уравнения обратились в тождества.
|
|
|
|
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 476; Нарушение авторских прав?; Мы поможем в написании вашей работы!