
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формулы приведения для тригонометрических функций
|
|
|
|
Формулы преобразования произведения в сумму
Тангенс сложения аргументов
Синус и косинус сложения аргументов
Тригонометрические функции числового аргумента.
Тригонометрические функции числового аргументаt – это функции вида y = cos t,
y = sin t, y = tg t, y = ctg t.
С помощью этих формул через известное значение одной тригонометрической функции можно найти неизвестные значения других тригонометрических функций.
Основные формулы тригонометрии:
sin (x + y) = sin x cos y + cos x sin y
sin (x – y) = sin x cos y – cos x sin y
cos (x + y) = cos x cos y – sin x sin y
cos (x – y) = cos x cos y + sin x sin y
Формулы двойного аргумента (двойного угла)
sin 2 x = 2 sin x cos x
cos 2 x = cos2 x – sin2 x
cos 2 x = 1 – 2 sin2 x
2 tg x
tg 2 x = ————
1 – tg2 x
tg x + tg y
tg (x + y) = ——————
1 – tg x tg y
tg x – tg y
tg (x – y) = ——————
1 + tg x tg y
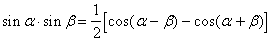
|
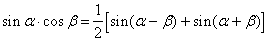
|
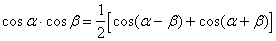
|
| j | 
| 
| 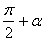
| 
| 
| 
| 
| 
| 
|
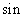 j j
| - 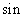 a a
| 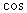 a a
| 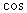 a a
| 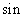 a a
| - 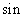 a a
| - 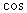 a a
| - 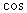 a a
| - 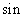 a a
| 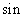 a a
|
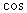 j j
| 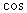 a a
| 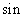 a a
| - 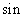 a a
| - 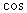 a a
| - 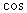 a a
| - 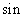 a a
| 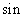 a a
| 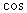 a a
| 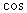 a a
|
 j j
| -  a a
| 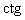 a a
| - 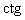 a a
| -  a a
|  a a
| 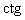 a a
| - 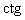 a a
| -  a a
|  a a
|
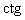 j j
| - 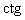 a a
|  a a
| -  a a
| - 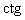 a a
| 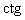 a a
|  a a
| -  a a
| - 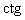 a a
| 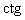 a a
|
Правило приведения:
| Для выражений π + t, π – t, 2π + t, 2π – t | Для выражений π/2 + t, π/2 – t, 3π/2 + t, 3π/2 – t |
| 1) В приведенном выражении следует сохранить тригонометрическую функцию преобразуемого выражения. 2) Перед полученной функцией следует поставить тот знак, который имела бы преобразуемая функция при условии, что 0 < t < π/2. | 1) В приведенном выражении следует изменить тригонометрическую функцию преобразуемого выражения на противоположную. 2) Перед полученной функцией следует поставить тот знак, который имела бы преобразуемая функция при условии, что 0 < t < π/2. |
Текст задания:
| Тригонометрические преобразования Вариант 1 | ||
| А) Выберите номер правильного ответа | ||
| А1 | Вычислите: 
| 1) 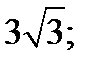 2) 2)  3) 3)  4) 4) 
|
| А2 | Найдите 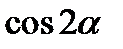 , если , если 
| 1) 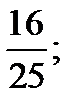 2) 2) 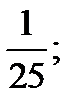 3) 3)  4) 4) 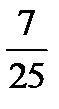
|
| А3 | Упростите выражение: 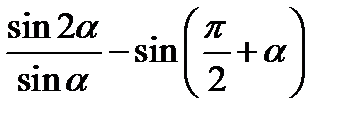
| 1)  2) 2)  3) 0; 4) 3) 0; 4) 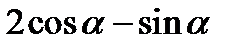
|
| А4 | Найдите значение выражения 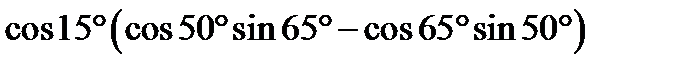
| 1)  2) 2) 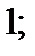 3) 3)  4) 4) 
|
| А5 | Упростите выражение: 
| 1) 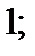 2) 2)  3) 3)  4) 4) 
|
| В) Напишите правильный ответ | ||
| В1 | Вычислите: 
| |
| В2 | Определите наибольшее значение выражения 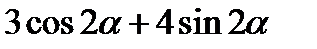
| |
| С) Приведите подробное решение данного задания. | ||
| С | Вычислите  , если , если 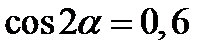 . .
|
|
|
|
| Тригонометрические преобразования Вариант 2 | ||
| А) Выберите номер правильного ответа | ||
| А1 | Вычислите: 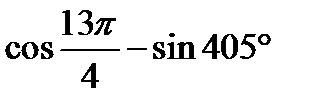
| 1) 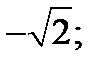 2) 2) 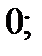 3) 3) 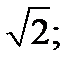 4) 4) 
|
| А2 | Найдите 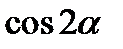 , если , если 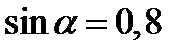
| 1)  2) 2) 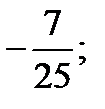 3) 3)  4) 4) 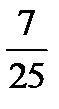
|
| А3 | Упростите выражение: 
| 1)  2) 2) 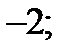 3) 0; 4) 3) 0; 4) 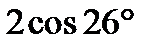
|
| А4 | Найдите значение выражения 
| 1)  2) 2) 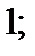 3) 3) 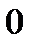 4) 4) 
|
| А5 | Упростите выражение: 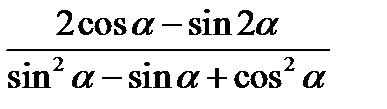
| 1)  2) 2)  3) 3)  4) 4) 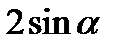
|
| В) Напишите правильный ответ | ||
| В1 | Вычислите: 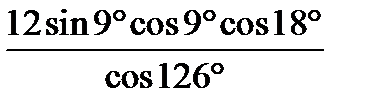
| |
| В2 | Определите наименьшее значение выражения 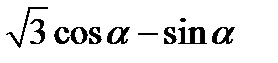
| |
| С) Приведите подробное решение данного задания. | ||
| С | Вычислите  , если , если 
|
| Тригонометрические преобразования Вариант 3 | ||
| А) Выберите номер правильного ответа | ||
| А1 | Вычислите: 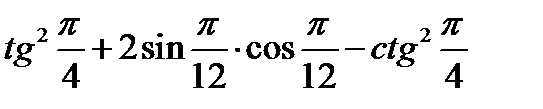
| 1)  2) 2)  3) 3) 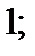 4) 4) 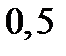
|
| А2 | Найдите  , если , если 
| 1)  2) 2) 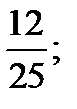 3) 3)  4) 4) 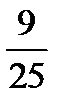
|
| А3 | Упростите выражение: 
| 1)  2) 2)  3) 1; 4) 3) 1; 4) 
|
| А4 | Найдите значение выражения 
| 1)  2) 2) 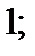 3) 3)  4) 4) 
|
| А5 | Упростите выражение: 
| 1) 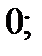 2) 2)  3) 3) 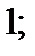 4) 4) 
|
| В) Напишите правильный ответ | ||
| В1 | Вычислите: 
| |
| В2 | Определите наибольшее значение выражения 
| |
| С) Приведите подробное решение данного задания. | ||
| С | Вычислите 
|
| Тригонометрические преобразования Вариант 4 | ||
| А) Выберите номер правильного ответа | ||
| А1 | Вычислите: 
| 1)  2) 2) 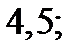 3) 3) 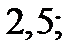 4) 4) 
|
| А2 | Найдите 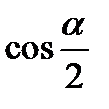 , если , если 
| 1)  2) 2) 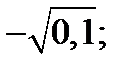 3) 3) 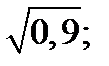 4) 4) 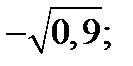
|
| А3 | Упростите выражение: 
| 1)  2) - 2) -  3) 1; 4) 3) 1; 4) 
|
| А4 | Найдите значение выражения 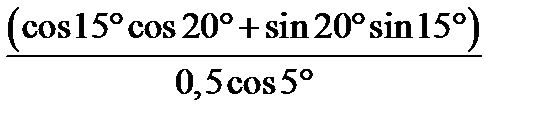
| 1) 2; 2) 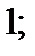 3) 3)  4) 4) 
|
| А5 | Упростите выражение: 
| 1) 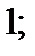 2) 2)  3) 3)  4) 4) 
|
| В) Напишите правильный ответ | ||
| В1 | Вычислите: 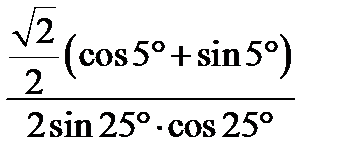
| |
| В2 | Определите наименьшее значение выражения 
| |
| С) Приведите подробное решение данного задания. | ||
| С | Вычислите: 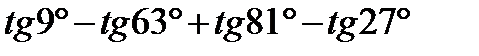
|
| Тригонометрические преобразования Вариант 5 | ||
| А) Выберите номер правильного ответа | ||
| А1 | Вычислите: 
| 1)  2) 2) 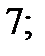 3) 3)  4) 4) 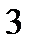
|
| А2 | Найдите 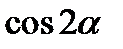 , если , если 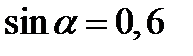
| 1) 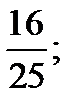 2) 2) 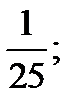 3) 3)  4) 4) 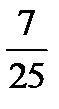
|
| А3 | Упростите выражение: 
| 1)  2) 2)  3) 3)  ; 4) 1 ; 4) 1
|
| А4 | Найдите значение выражения 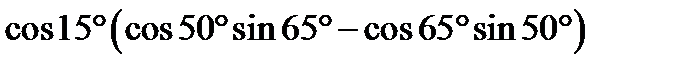
| 1)  2) 2) 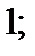 3) 3)  4) 4) 
|
| А5 | Упростите выражение: 
| 1) 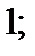 2) 2)  3) 3)  4) 4) 
|
| В) Напишите правильный ответ | ||
| В1 | Вычислите: 
| |
| В2 | Определите наибольшее значение выражения 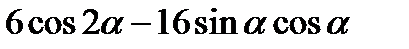
| |
| С) Приведите подробное решение данного задания. | ||
| С | Вычислите  , если , если 
|
|
|
|
| Тригонометрические преобразования Вариант 6 | ||
| А) Выберите номер правильного ответа | ||
| А1 | Вычислите: 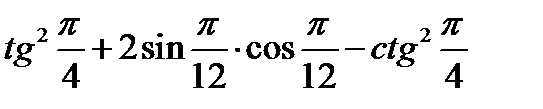
| 1)  2) 2)  3) 3) 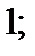 4) 4) 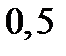
|
| А2 | Найдите 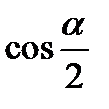 , если , если 
| 1) 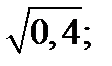 2) 2)  3) 3) 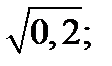 4) 4) 
|
| А3 | Упростите выражение: 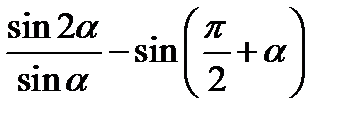
| 1)  2) 2)  3) 0; 4) 3) 0; 4) 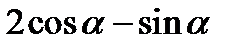
|
| А4 | Найдите значение выражения 
| 1)  2) 2) 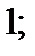 3) 3) 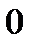 4) 4) 
|
| А5 | Упростите выражение: 
| 1) 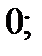 2) 2) 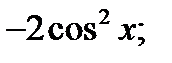 3) 3) 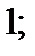 4) 4) 
|
| В) Напишите правильный ответ | ||
| В1 | Вычислите: 
| |
| В2 | Определите наибольшее значение выражения 
| |
| С) Приведите подробное решение данного задания. | ||
| С | Вычислите 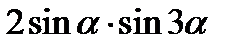 , если , если 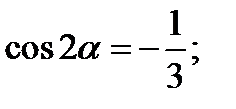
|
Практическая работа № 11
Тема: Тригонометрические функции их графики и свойства
Цель работы: закрепить знания и умения студентов по освоению свойств тригонометрических функций.
Теоритическое обоснование:
Функции y = sin x, y = cos x, y = mf(x), y = f(kx), y = tg x, y = ctg x
Функция y = sin x
Графиком функции является синусоида.
Полную неповторяющуюся часть синусоиды называют волной синусоиды.
Половину волны синусоиды называют полуволной синусоиды (или аркой).
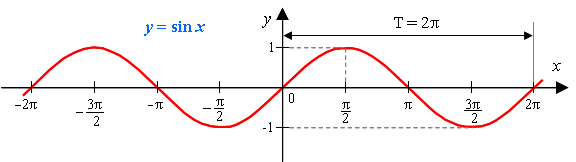
Свойства функции y = sin x:
| 1) Область определения функции – множество действительных чисел. 2) Область значений функции – отрезок [–1; 1] 3) Это нечетная функция. 4) Это непрерывная функция. 5) Координаты точек пересечения графика: - с осью абсцисс: (πn; 0), - с осью ординат: (0; 0). 6) На отрезке [-π/2; π/2] функция возрастает, на отрезке [π/2; 3π/2] – убывает. 7) На промежутках [2πn; π + 2πn] функция принимает положительные значения. На промежутках [-π + 2πn; 2πn] функция принимает отрицательные значения. 8) Промежутки возрастания функции: [-π/2 + 2πn; π/2 + 2πn]. Промежутки убывания функции: [π/2 + 2πn; 3π/2 + 2πn]. 9) Точки минимума функции: -π/2 + 2πn. Точки максимума функции: π/2 + 2πn 10) Функция ограничена сверху и снизу. Наименьшее значение функции –1, наибольшее значение 1. 11) Это периодическая функция с периодом 2π (Т = 2π) |
Для построения графика функции y = sin x удобно применять следующие масштабы:
- на листе в клетку за единицу отрезка примем длину в две клетки.
|
|
|
- на оси x отмерим длину π. При этом для удобства 3,14 представим в виде 3 – то есть без дроби. Тогда на листе в клетку π составит 6 клеток (трижды по 2 клетки). А каждая клетка получит свое закономерное имя (от первой до шестой): π/6, π/3, π/2, 2π/3, 5π/6, π. Это значения x.
- на оси y отметим 1, включающий две клетки.
Составим таблицу значений функции, применяя наши значения x:
| x | π — 6 | π — 3 | π — 2 | 2π — 3 | 5π — 6 | π | |
| y | 0 | 1 — 2 | √3 — 2 | 1 | √3 — 2 | 1 — 2 | 0 |
Далее составим график. Получится полуволна, наивысшая точка которой (π/2; 1). Это график функции y = sin x на отрезке [0; π]. Добавим к построенному графику симметричную полуволну (симметричную относительно начала координат, то есть на отрезке -π). Гребень этой полуволны – под осью x с координатами (-1; -1). В результате получится волна. Это график функции y = sin x на отрезке [-π; π].
Можно продолжить волну, построив ее и на отрезке [π; 3π], [π; 5π], [π; 7π] и т.д. На всех этих отрезках график функции будет выглядеть так же, как на отрезке [-π; π]. Получится непрерывная волнистая линия с одинаковыми волнами.
Функция y = cos x.
Графиком функции является синусоида (ее иногда называют косинусоидой).

Свойства функции y = cos x:
| 1) Область определения функции – множество действительных чисел. 2) Область значений функции – отрезок [–1; 1] 3) Это четная функция. 4) Это непрерывная функция. 5) Координаты точек пересечения графика: - с осью абсцисс: (π/2 + πn; 0), - с осью ординат: (0;1). 6) На отрезке [0; π] функция убывает, на отрезке [π; 2π] – возрастает. 7) На промежутках [-π/2 + 2πn; π/2 + 2πn] функция принимает положительные значения. На промежутках [π/2 + 2πn; 3π/2 + 2πn] функция принимает отрицательные значения. 8) Промежутки возрастания: [-π + 2πn; 2πn]. Промежутки убывания: [2πn; π + 2πn]; 9) Точки минимума функции: π + 2πn. Точки максимума функции: 2πn. 10) Функция ограничена сверху и снизу. Наименьшее значение функции –1, наибольшее значение 1. 11) Это периодическая функция с периодом 2π (Т = 2π) |
Функция y = mf (x).
|
|
|
Возьмем предыдущую функцию y = cos x. Как вы уже знаете, ее графиком является синусоида. Если мы умножим косинус этой функции на определенное число m, то волна растянется от оси x (либо сожмется, в зависимости от величины m).
Эта новая волна и будет графиком функции y = mf(x), где m – любое действительное число.
Таким образом, функция y = mf(x) – это привычная нам функция y = f(x), умноженная на m.
Если m < 1, то синусоида сжимается к оси x на коэффициент m. Если m > 1, то синусоида растягивается от оси x на коэффициент m.
Выполняя растяжение или сжатие, можно сначала построить лишь одну полуволну синусоиды, а затем уже достроить весь график.
Функция y = f (kx).
Если функция y = mf (x) приводит к растяжению синусоиды от оси x либо сжатию к оси x, то функция y = f(kx) приводит к растяжению от оси y либо сжатию к оси y.
Причем k – любое действительное число.
При 0 < k < 1 синусоида растягивается от оси y на коэффициент k. Если k > 1, то синусоида сжимается к оси y на коэффициент k.
Составляя график этой функции, можно сначала построить одну полуволну синусоиды, а по ней достроить затем весь график.
Функция y = tg x.
Графиком функции y = tg x является тангенсоида.
Достаточно построить часть графика на промежутке от 0 до π/2, а затем можно симметрично продолжить ее на промежутке от 0 до 3π/2.

Свойства функции y = tg x:
| 1) Область определения функции – множество всех действительных чисел, кроме чисел вида x = π/2 + πk, где k – любое целое число. Это означает, что на графике функции нет точки, принадлежащей прямой x = π/2, либо прямой x = 3π/2, либо прямой x = 5π/2, либо прямой x = –π/2 и т.д. 2) Область значений функции (–∞; +∞) 3) Это нечетная функция. 4) Это непрерывная функция на интервале (–π/2; π/2). 5) Это периодическая функция с основным периодом π (Т = π) 6) Функция возрастает на интервале (–π/2; π/2). 7) Функция не ограничена ни сверху, ни снизу. Не имеет ни наименьшего, ни наибольшего значений. |
Функция y = ctg x
Графиком функции y = ctg x также является тангенсоида (ее иногда называют котангенсоидой).
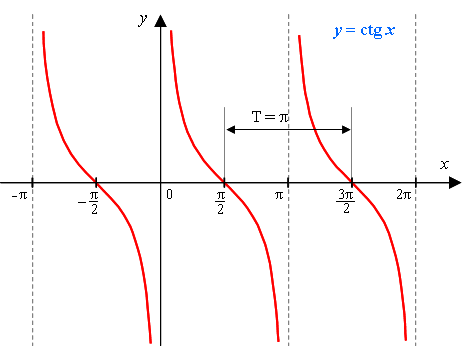
Свойства функции y = ctg x:
| 1) Область определения функции – множество всех действительных чисел, кроме чисел вида x = πk, где k – любое целое число. 2) Область значений функции (–∞; +∞) 3) Это нечетная функция. 4) Это непрерывная функция. 5) Это периодическая функция с основным периодом π (Т = π) 6) Функция убывает в промежутке (πk; π + πk), где k – любое целое число. 7) Функция не ограничена ни сверху, ни снизу. Не имеет ни наименьшего, ни наибольшего значений. |
Текст задания:
| Множество значений | ||
| А1 | Определите множество значений функции:
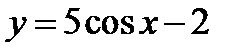
| 1)  ; 2) ; 2) 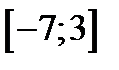 ; 3) ; 3)  ; 4) ; 4) 
|
| А2 | Найдите сумму целых значений функции
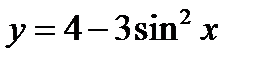
| 1) 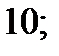 2) 2)  3) 3) 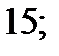 4) 4) 
|
| А3 | Укажите наибольшее целое значение функции 
| 1)  2) 2)  3) 3)  4) 4) 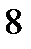
|
| А4 | Определите множество значений функции:
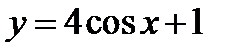
| 1) 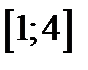 ; 2) ; 2)  ; 3) ; 3) 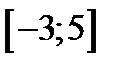 ; 4) ; 4) 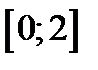
|
| А5 | Найдите сумму целых значений функции

| 1)  2) 2) 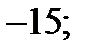 3) 3) 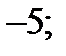 4) 4) 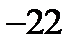
|
| А6 | Укажите наименьшее целое значение функции 
| 1)  2) 2)  3) 3)  4) 4) 
|
| А7 | Определите множество значений функции:

| 1)  ; 2) ; 2)  ; 3) ; 3) 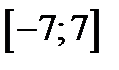 ; 4) ; 4) 
|
| А8 | Найдите сумму целых значений функции

| 1)  2) 2) 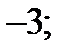 3) 3)  4) 4) 
|
| А9 | Укажите наибольшее целое значение функции 
| 1)  2) 2)  3) 3)  4) 4) 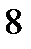
|
| А10 | Определите множество значений функции:
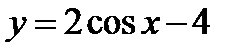
| 1) 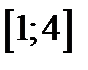 ; 2) ; 2) 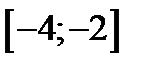 ; 3) ; 3) 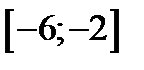 ; 4) ; 4) 
|
| А11 | Найдите сумму целых значений функции

| 1) 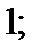 2) 2)  3) 3) 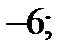 4) 4) 
|
| А12 | Укажите наименьшее целое значение функции 
| 1) 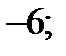 2) 2)  3) 3)  4) 4) 
|
Практическая работа № 12
Тема: Решение простейших тригонометрических уравнений и неравенств
Цель работы: закрепить знания и умения студентов по освоению формул.
Теоритическое обоснование:
Решение простейших тригонометрических уравнений
| Уравнение | Общее решение | Частные случаи | ||

| 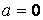
| 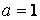
| ||
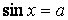 , ,
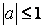
| 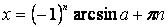
| 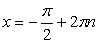
| 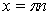
| 
|
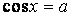 , ,
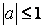
| 
| 
| 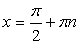
| 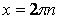
|
 , ,
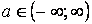
| 
| 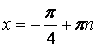
| 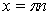
| 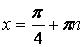
|
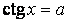 , ,
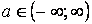
| 
| 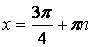
| 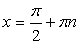
| 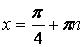
|
Текст задания:





Практическая работа № 13
Тема: Решение тригонометрических уравнений и неравенств
Цель работы: закрепить знания и умения студентов по освоению методов решения тригонометрических уравнений и неравенств.
Теоритическое обоснование:
1. Решение тригонометрических уравнений
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 1781; Нарушение авторских прав?; Мы поможем в написании вашей работы!