Производные высших порядков

Применение дифференциала для приближенных вычислений.

6).

Основные свойства дифференциала

.

.

Понятие дифференциала.

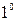Пусть функция 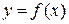имеет в точке 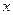конечную производную 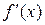, тогда ее приращение можно записать в виде

,

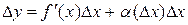где .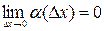

Главная, линейная относительно 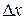часть 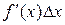приращения функции называется дифференциалом функции и обозначается :

При 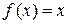, получим 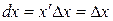, поэтому дифференциал функции 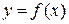примет вид

1) где 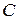= const,

2)

3) ,

4) ,

5)

При достаточно малых 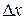приращение функции приближенно равно ее дифференциалу, т. е. и

.

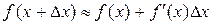Пример 9. Найти дифференциал функции .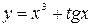

Решение. Найдем производную данной функции .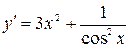

Следовательно, по определению дифференциала функции получим

.

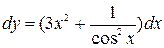Пример1 0. Вычислить с помощью дифференциала приближенное значение

Решение. Рассмотрим функцию 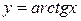. Пологая 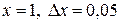и применяя формулу , получим

.

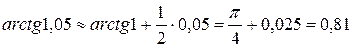Производной второго порядка (второй производной) функции 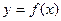называется производная от производной 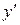. Вторая производная обозначается так: , или , или .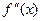

Если 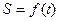- закон прямолинейного движения точки, то вторая производная пути по времени 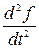есть ускорение этого движения.

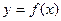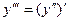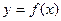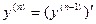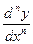Аналогично производная третьего порядка функции есть производная производной второго порядка и т.д., производной n -го порядка от функции называется производная от производной -го порядка . Обозначается n -я производная так: или , или .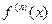

Пример 10. Дана функция .

Найти: , , ,…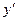

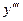Дата добавления: 2014-12-16