Вычисление определителей методом элементарных преобразований

Теорема Лапласа

Пусть A – квадратная матрица n -го порядка.
Определитель k -го порядка, составленный из элементов матрицы A, расположенных на пересечении строк с номерами i ₁, i ₂,..., i_k и столбцов с номерами j ₁, j ₂,..., j_k, называется минором M k -го порядка матрицы A.

Если из матрицы A вычеркнуть строки и столбцы с такими номерами, то определитель n–k -го порядка полученной матрицы называется дополнительным минором для минора M.

Обозначим символом S сумму индексов, нумерующих строки и столбцы такого минора:

S = i ₁ + j ₁ + i ₂ + j ₂ +... + i_k + j_k.

Алгебраическим дополнением минора M называется дополнительный минор для минора M, умноженный на (–1) ^S.

Отметим, что алгебраическое дополнение A_{i j} элемента a_{i j} (минора первого порядка) является частным случаем алгебраического дополнения минора.

Теорема Лапласа. Пусть D – определитель n -го порядка, в котором произвольно выбраны k строк (или столбцов), где 1 ≤ k ≤ n – 1.
Тогда определитель D равен сумме произведений всех миноров k -го порядка, расположенных в выбранных строках (или столбцах), на их алгебраические дополнения.

Под элементарными преобразованиями определителей понимаются следующие операции.

N	Операция	Результат
	Перестановка местами двух строк или столбцов определителя.	Определитель изменяет свой знак на противоположный.
	Умножение элементов строки или столбца на ненулевое число c.	Определитель умножается на число c.
	Прибавление к строке другой строки, предварительно умноженной на любое число.	Определитель не изменяется.

Целью таких преобразований является приведение определителя к треугольному виду, что решает проблему его вычисления.

Можно поступать и несколько иначе: с помощью элементарных преобразований получить строку (или столбец), содержащую только один ненулевой элемент, и затем разложить полученный определитель по элементам этой строки (столбца).
Подобная процедура понижает порядок определителя на одну единицу.

Примеры:

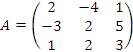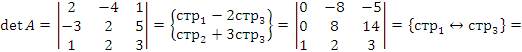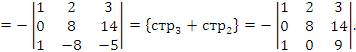1. Вычислить определитель матрицы приведением к треугольному виду. Решение. Определитель матрицы треугольного вида равен произведению ее диагональных элементов. Следовательно,

***

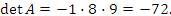
2. Вычислить определитель матрицы 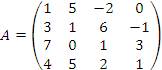Решение. Сначала преобразуем первую строку с помощью элементарных операций над столбцами, стремясь получить в ней максимально возможное число нулей. С этой целью вычтем из второго столбца пятый столбец, предварительно умноженный на 5, а к третьему столбцу прибавим удвоенный второй столбец: 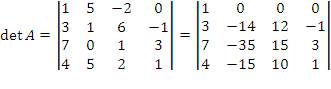Затем произведем разложение определителя по элементам первой строки: 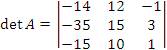Преобразуем строки, прибавляя к первой строке третью и вычитая из второй строки утроенную третью: 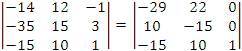Произведем разложение определителя по элементам третьего столбца:

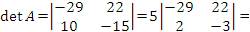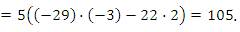
Дата добавления: 2014-12-16