Основные определения и аксиомы статики

Естественный способ задания движения точки

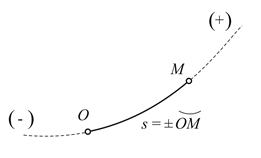
Рис.1.6

Пусть траектория точки заранее известна. Рассматривая траекторию как криволинейную координатную ось, примем любую точку 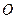траектории за начало отсчета и установим положительное и отрицательное направления отсчета. 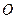Положение точки однозначно определяется дуговой координатой, которая равна взятой с соответствующим знаком длине дуги траектории, отделяющей в данный момент времени точку от начала отсчета (Рис.1.6). Движение точки будет задано, если задана зависимость дуговой координаты от времени: Описанный способ задания движения называется естественным.

1.8. Естественный трехгранник

Пусть точка движется по траектории , на которой установлена криволинейная система отсчета (Рис.1.7).

Рис.1.7

В любой точке траектории существует единственная касательная. Обозначим единичный вектор касательной; направлен в сторону возрастания дуговой координаты. Нормаль, лежащая в соприкасающейся плоскости, называется главной нормалью. Обозначим 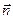единичный вектор главной нормали; 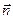направлен в сторону вогнутости траектории. Нормаль, перпендикулярная соприкасающейся плоскости, называется бинормалью. Её единичный вектор направлен так, чтобы векторы 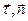и образовывали правую тройку.

Соприкасающаяся, нормальная и спрямляющая плоскости образуют естественный трехгранник. Касательная, главная нормаль и бинормаль – оси естественного трехгранника; 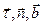– орты этих осей.

Оси естественного трехгранника играют существенную роль в описании движения точки, поскольку в этих осях вектор скорости и вектор ускорения вычисляются, как будет показано ниже, наиболее удобным образом. Пока отметим только, что разложение этих векторов по осям естественного трехгранника имеет вид:

(1.8)

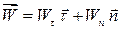(1.9)

где

– проекция вектора скорости на направление касательной к траектории;

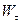– проекция вектора ускорения на направление касательной к траектории, которая называется касательным ускорением точки;

– проекция вектора ускорения точки на направление главной нормали к траектории точки, которая называется нормальным ускорением точки.

Оставляя доказательство для самостоятельного изучения, приведём окончательные результаты.

Для вектора скорости получаем:

(1.10)

Таким образом,

проекция вектора скорости на направление касательной к траектории точки равна первой производной по времени от дуговой координаты:

(1.12)

Для вектора ускорения получаем:

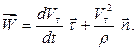(1.13)

Следовательно, касательное и нормальное ускорения точки определяются по формулам:

(1.14)

Здесь 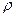– радиус кривизны траектории в данной точке.

Ускорение точки характеризует изменение вектора скорости. В общем случае вектор скорости может изменять свой модуль и свое направление.

Рассмотрим движение, при котором вектор скорости может изменять свое направление (траектория точки – любая кривая), но модуль скорости остается при этом постоянным. Такое движение называется равномерным. Как видно из формул (1.14) касательное ускорение в этом случае равно нулю. При неравномерном движении касательное ускорение обращается в нуль только в те моменты времени, когда модуль скорости достигает экстремальных значений. Таким образом, касательное ускорение характеризует изменение модуля скорости точки.

Вычисление скорости точки при естественном способе задания ее движения

(Изучить самостоятельно)

Пусть движение точки задано естественным способом. За промежуток времени 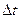точка переместится по траектории из положения в положение .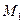

Используя определение вектора скорости, получаем:

Предел отношения длины дуги к длине стягивающей ее хорды по модулю равен единице. Если точка движется в положительном направлении, 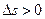и вектор 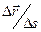совпадает по направлению с вектором . Если точка движется в отрицательном направлении отсчета, и вектор 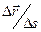противоположен по направлению вектору . В обоих случаях предельное направление вектора 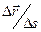совпадает с направлением единичного вектора касательной . Таким образом,

Принимая во внимание, что 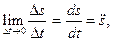получаем:

Вычисление ускорения точки при естественном способе задания ее движения

(Изучить самостоятельно)

Используя определение вектора ускорения (1.6) и формулу (2.1), получаем:

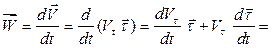
         (а)

Вычислим вектор 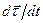. Прежде всего, найдем направление этого вектора. Рассмотрим тождество

Дифференцируя это тождество по скалярному аргументу , получаем:

или

Но 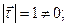в общем случае вектор изменяет со временем свое направление, так что 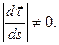Следовательно, скалярное произведение обратилось в нуль потому, что сомножители взаимно перпендикулярны.

Таким образом, вектор 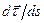перпендикулярен касательной, т.е. направлен по нормали к траектории. Ранее было показано, что вектор ускорения лежит в соприкасающейся плоскости. Следовательно, речь идет о главной нормали. Таким образом,

(б)

Остается вычислить

Пусть и 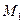две близкие точки траектории. В точке проведем главную нормаль 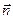В точке 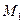построим нормаль 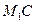, пересекающую в точке 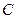главную нормаль, построенную в точке (если траектория плоская кривая, то 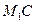также будет главной нормалью). Угол между двумя близкими касательными, угол 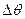, называется углом смежности. В силу близости точек и 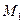угол между нормалям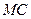и и 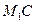приближенно равен углу 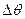(для плоской кривой это равенство точное). В силу малости дугу 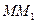можно считать дугой окружности радиуса 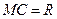. Тогда 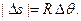Из равнобедренного треугольника определяем

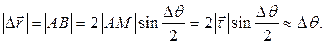
Тогда

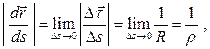
где 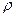— предельное значение радиуса окружности, дуга которой в бесконечно малой окрестности точки совпадает с дугой траектории. Эта окружность расположена в соприкасающейся плоскости, построенной для точки . Ее центр лежит на главной нормали и называется центром кривизны траектории в точке . Ее радиус 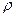называется радиусом кривизны траектории в точке .

Окончательно получаем:

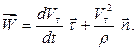
Совокупность приложенных к телу сил называется системой сил.

Дата добавления: 2014-12-16