Доказательство

Необходимость. Нам дано, что связный граф G является деревом. Нужно доказать, что в нем количество вершин ровно на единицу больше количества его ребер.

Рассмотрим это дерево, как корневое (выберем какую-нибудь вершину в качестве корня и распределим вершины по уровням (ярусам)). Рассмотрим теперь ориентированное дерево G’, порожденное деревом G. У каждого ребра дерева G’ одна и только одна конечная вершина. Следовательно число вершин и ребер G’ (а, значит, и G)одно и то же, исключая корневую вершину. Если учесть и корневую вершину, то количество вершин окажется на единицу больше количества ребер и необходимость теоремы доказана.

Достаточность. Нам дано, что в связном графе G количество вершин ровно на единицу больше количества ребер. Нужно доказать, что G – дерево.

Если G содержит цикл С: a,v₁,v₂v₃, …,v _n-1, a, то зафиксируем в этом цикле произвольное ребро (v_i,v_j). Тогда (см. доказательство достаточности первого критерия дерева) существуют две цепи соединяющих вершины v_i и v_j. Удалим ребро (v_i,v_j) из G. Тем самым мы разрываем цикл и не нарушаем связности графа (ибо одна из цепей, соединяющих вершины v_i и v_j, сохранится). Если в полученном графе существуют циклы, то разорвем их аналогично предыдущему. В результате получим дерево G’ у которого (согласно доказательству необходимости теоремы) количество вершин ровно на единицу больше количества ребер. Пусть количество вершин графа G равно m, а количество его ребер равно n. Пусть еще при переходе от графа G к дереву G’ нами отброшено k ребер. Тогда в G’ количество ребер равно n- k, а количество вершин равно m (вершины графа G при переходе к дереву G’ не затрагивались). По условию в связном графе G количество вершин ровно на единицу больше количества ребер, т.е. m = n + 1. С другой стороны, для дерева G’ имеем m = n – k + 1. Таким образом, n +1 = n – k + 1. Откуда k = 0. Поэтому при переходе от графа G к дереву G’ не было отброшено ни одно ребро, а значит, исходный граф G - дерево. Что и требовалось доказать в достаточности теоремы.

Дерево G’, построенное из графа G в проведенном выше доказательстве достаточности второго критерия дерева, называется остовным или каркасным деревом графа G. Дадим более формальное определение.

Определение 5.4. Дерево G’ называется остовным (или каркасным) деревом графа G, если G’ ⥹ G ( G’ подграф графа G )и V’ = V.

Определение 5.5. Наименьшее (минимальное) количество ребер графа G, которые нужно удалить из него для того чтобы превратить граф в дерево или лес (т.е., чтобы разорвать все имеющиеся в нем циклы), называется цикломатическим числом графа и обозначается ν( G).

Теорема 5.3. Для цикломатического числа ν( G) графа G = (V,U), справедлива формула

ν( G) = | U | - | V | + K(G),

где K(G) - количество компонент связности графа.

Доказательство. Зафиксируем в исходном графе G произвольную компоненту связности G_i. Преобразуем ее в дерево G_i’ (аналогично процедуре, примененной при доказательстве достаточности предыдущей теоремы). Заметим, что при этом нам придется удалить из G_i количество ребер, равное ν(G_i). В силу теоремы 5.2 имеем:

| V_Gi’ | = | U_Gi’ | +1 = | U_Gi | - ν(G_i) + 1, или ν(G_i) = | U_Gi | - | V_Gi’ |+ 1.

Учтем теперь, что | V_Gi’ |=| V_{G i} | и соберем результаты по всем компонентам связности исходного графа. Получим:

.

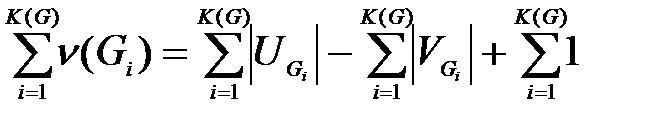Таким образом, общее минимальное количество ребер, отброшенных на переходе от исходного графа G к лесу (или дереву) G’ (т.е. ν(G)) равно:

ν(G) = | U | - | V | + K(G),

где K(G) - количество компонент связности графа G, что и требовалось доказать.

Пример 5.2. Пусть нам задан граф

v₁ v₂ v₃ v₄ v₅

G:

v₆ v₇ v₈ v₉ v₁₀

Тогда, например, его подграф

v₁ v₂ v₃ v₄ v₅

G’:

v₆ v₇ v₈ v₉ v₁₀

является остовным деревом исходного графа G. ν(G) =5.

Дата добавления: 2014-12-16