
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Извлечение корня й степени из комплексного числа. Множества в комплексной плоскости
|
|
|
|
Равенство (1) называется формулой Муавра. Используя его, можно вывести формулу извлечения корня 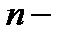 й степени из комплексного числа. Однако для этого надо ввести сначала понятие корня.
й степени из комплексного числа. Однако для этого надо ввести сначала понятие корня.
Определение 1. Корнем 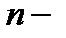 й степени из комплексного числа
й степени из комплексного числа 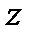 называется такое комплексное число
называется такое комплексное число 
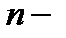 я степень которого равна
я степень которого равна  Обозначение:
Обозначение: 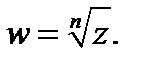 Таким образом,
Таким образом, 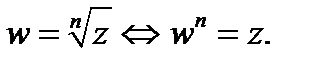
Пусть  Имеем (при
Имеем (при 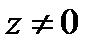 )
)
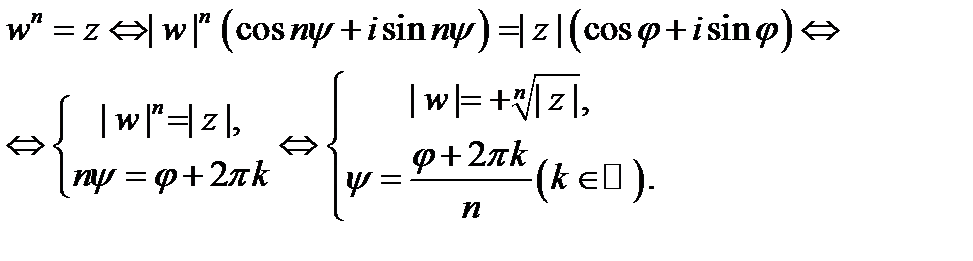
Значит, 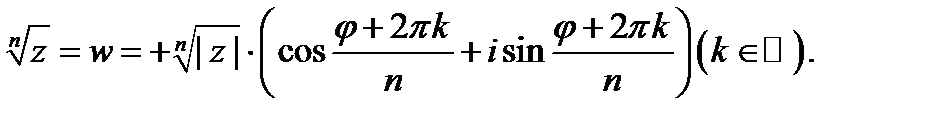 Изменяя здесь
Изменяя здесь 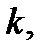 видим, что различные значения корня
видим, что различные значения корня 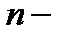 й степени получаются при
й степени получаются при  Дальнейшее изменение
Дальнейшее изменение  привело бы к уже полученным значениям
привело бы к уже полученным значениям 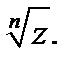 Если же
Если же 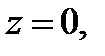 то, очевидно,
то, очевидно,  Мы доказали следующий результат.
Мы доказали следующий результат.
Теорема 1. Если 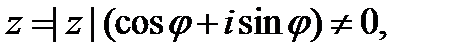 то корень
то корень 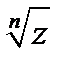 имеет ровно
имеет ровно 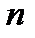 различных значений:
различных значений:  Если
Если 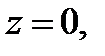 то
то  имеет только одно значение, равное нулю.
имеет только одно значение, равное нулю.
Например,
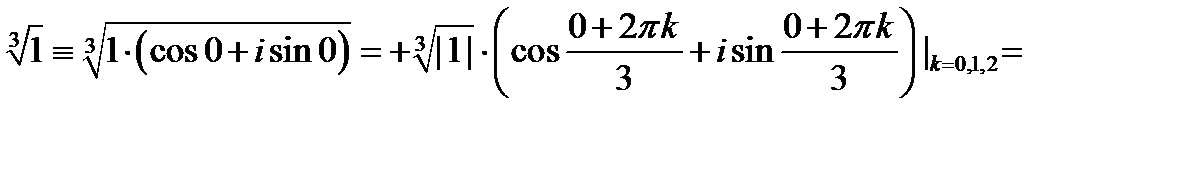
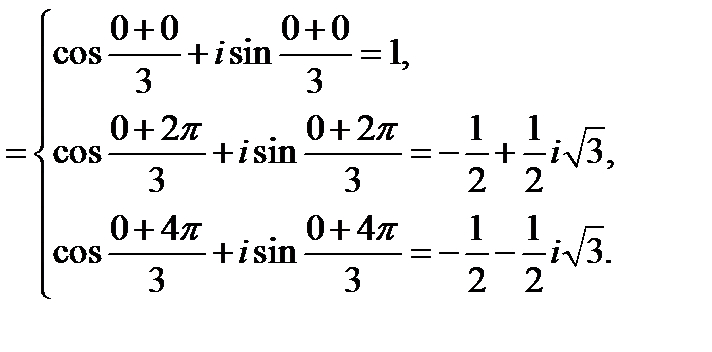
Приведем примеры простейших множеств точек на комплексной плоскости:
а) 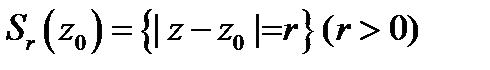 -- окружность с центром в точке
-- окружность с центром в точке 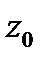 радиусом
радиусом 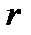 ;
;
б)  -- открытый круг с центром в точке
-- открытый круг с центром в точке  радиусом
радиусом 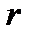 ;
;
в)  -- внешность открытого круга с центром в точке
-- внешность открытого круга с центром в точке  радиусом
радиусом 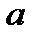 ;
;
г)  -- открытое кольцо с центром в точке
-- открытое кольцо с центром в точке  ;
;
д) 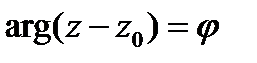 -- луч с началом в точке
-- луч с началом в точке  , идущий под углом
, идущий под углом 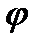 к положительному направлению действительной оси;
к положительному направлению действительной оси;
е) 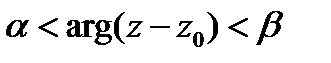 -- внутренность неограниченного открытого сектора с вершиной в точке
-- внутренность неограниченного открытого сектора с вершиной в точке 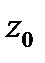 и углом
и углом 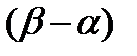 ;
;
ж) 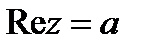 -- прямая, параллельная мнимой оси, проходящая через точку
-- прямая, параллельная мнимой оси, проходящая через точку 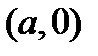 ;
;
з) 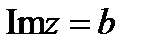 -- прямая, параллельная действительной оси, проходящая через точку
-- прямая, параллельная действительной оси, проходящая через точку 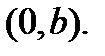
и)  вертикальная полоса между прямыми
вертикальная полоса между прямыми  и
и 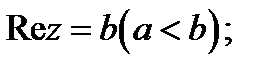
к) 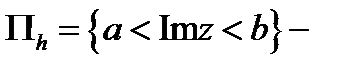 горизонтальная полоса между прямыми
горизонтальная полоса между прямыми  и
и 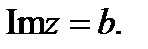

 Рекомендуем сделать рисунки всех перечисленных множеств. В качестве упражнения попробуйте записать аналитически (в виде уравнений или неравенств) приводимые ниже множества на комплексной плоскости[3]
Рекомендуем сделать рисунки всех перечисленных множеств. В качестве упражнения попробуйте записать аналитически (в виде уравнений или неравенств) приводимые ниже множества на комплексной плоскости[3]


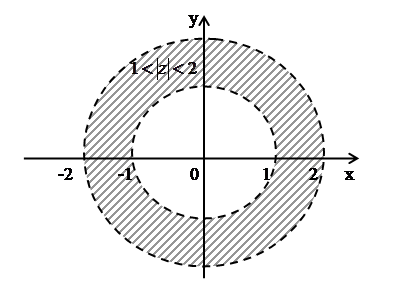

Рис. 2
Понятие окрестности точки вводится также, как и в действительном анализе.
|
|
|
Определение 2.  окрестностью точки
окрестностью точки 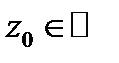 называется открытый круг
называется открытый круг
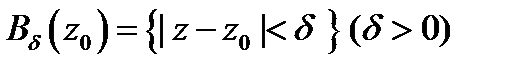
с центром в точке  радиуса. Проколотой
радиуса. Проколотой 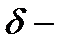 окрестностью точки
окрестностью точки 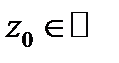 называется множество
называется множество 
Определение 3. Точка  называется внутренней точкой множества
называется внутренней точкой множества  если она входит в
если она входит в 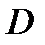 вместе с некоторой своей окрестностью. Если все точки множества
вместе с некоторой своей окрестностью. Если все точки множества  внутренние, то
внутренние, то  называется открытым множеством.
называется открытым множеством.
Определение 4. Точка  называется граничной точкой множества
называется граничной точкой множества 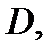 если в любой окрестности этой точки имеются как точки, принадлежащие
если в любой окрестности этой точки имеются как точки, принадлежащие 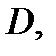 так и точки, не принадлежащие
так и точки, не принадлежащие  Множество всех граничных точек
Множество всех граничных точек 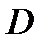 образует границу
образует границу 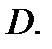 Обозначение:
Обозначение: 
Определение 5. Множество 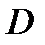 называется связным, если любые две его точки можно соединить непрерывной кривой, не выходя из
называется связным, если любые две его точки можно соединить непрерывной кривой, не выходя из 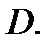 Множество
Множество 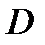 называется односвязным, если любой замкнутый контур, лежащий в
называется односвязным, если любой замкнутый контур, лежащий в 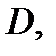 можно стянуть в точку, не выходя из
можно стянуть в точку, не выходя из  И, наконец, множество
И, наконец, множество 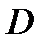 называется
называется 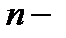 связным, если его граница
связным, если его граница 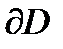 состоит из
состоит из  попарно не пересекающихся между собой замкнутых контуров.
попарно не пересекающихся между собой замкнутых контуров.
Определение 6. Любое открытое связное множество называется областью. Область 
 называется ограниченной, если существует круг, охватывающий область
называется ограниченной, если существует круг, охватывающий область 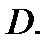 В противном случае область
В противном случае область  называется не ограниченной.
называется не ограниченной.
Пусть  и
и 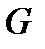 две области на комплексной плоскости
две области на комплексной плоскости  причем
причем  находится в плоскости
находится в плоскости 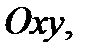 а
а  в плоскости
в плоскости 
Определение 7. Говорят, что задана функция 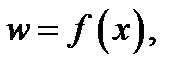 отображающая область
отображающая область  в область
в область  если каждому числу
если каждому числу 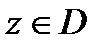 поставлено в соответствие одно или несколько комплексных чисел
поставлено в соответствие одно или несколько комплексных чисел 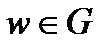 по закону
по закону  При этом
При этом  называется областью определения функции
называется областью определения функции 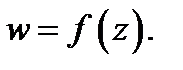 Если каждому
Если каждому  поставлено в соответствие единственное число
поставлено в соответствие единственное число 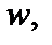 то говорят, что функция
то говорят, что функция  однозначна; в противном случае функция
однозначна; в противном случае функция 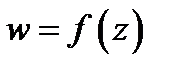 многозначна. Функция называется однолистной в области
многозначна. Функция называется однолистной в области 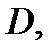 если
если
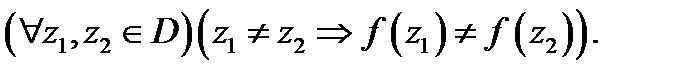
Например, функция 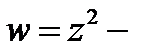 однозначная, но не однолистная, а функция
однозначная, но не однолистная, а функция  трёхзначная. Функция
трёхзначная. Функция 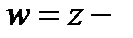 однозначная и однолистная.
однозначная и однолистная.
Поскольку каждое комплексное число вполне определяется своей действительной и мнимой частью, то функцию  комплексной переменной можно записать в виде
комплексной переменной можно записать в виде
|
|
|

Например, функцию  можно записать в указанном виде, если в ней выделить действительную и мнимую части:
можно записать в указанном виде, если в ней выделить действительную и мнимую части:  Здесь
Здесь 

Частные типы комплексных функций:
а) комплексная последовательность: 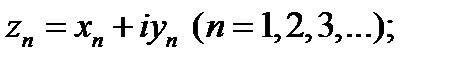
б) комплексная функция действительного аргумента: 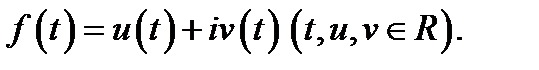
С последней функцией мы встречались в главе 4 при рассмотрении комплексных решений дифференциальных уравнений. Такие функции часто используются при задании кривых в комплексной плоскости. Например, уравнение  описывает уравнение окружности в плоскости
описывает уравнение окружности в плоскости  радиуса
радиуса 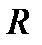 и с центром в точке
и с центром в точке 
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 673; Нарушение авторских прав?; Мы поможем в написании вашей работы!