Структурное программирование сверху-вниз: дополнительные соображения 2 страница

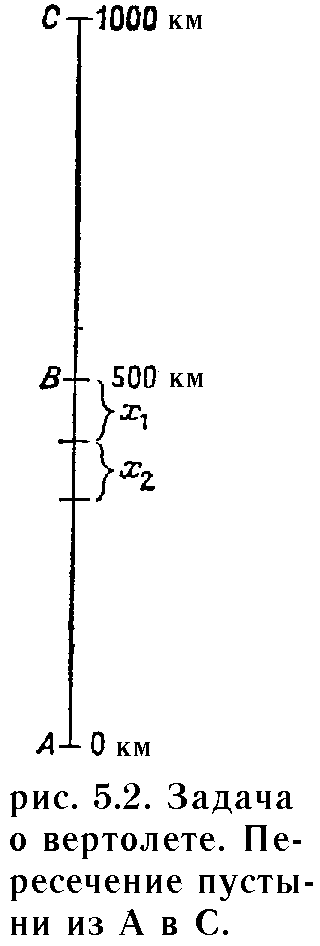
Подойдем к этой задаче с помощью метода отрабатывания назад. На какое расстояние от конца мы сможем пересечь пустыню, имея за­пас горючего в точности на k баков? Мы будем задавать этот вопрос для k=1, 2, 3,..., пока не найдем такое целое п, что п полных баков позволят пересечь всю 1000-километровную пустыню.

Для k=1 ответ равен 500 милям, как и показано на рис. 5.2. Можно заправить машину в точке В и пересечь оставшиеся 500 километров пустыни. Ясно, что это наиболее отдаленная точка, стартуя из которой можно преодолеть пустыню, имея в точности 500 литров горючего.

Мы поставили перед собой частную цель, потому что не смогли бы решить сразу исходную задачу. Мы не задаем вопрос: сколько топлива нужно вертолету, чтобы преодолеть заданную дистанцию? Вместо этого задаем более простой, но родственный вопрос: какое расстояние можно пролететь на заданном количестве топлива? Ответить на первый вопрос становится воз­можным, когда ответом на второй является: не мень­ше 1000 километров.

Предположим, что k=2, т. е. имеется два полных бака (1000 литров). Будем рассматривать этот слу­чай, опираясь на результат для k=1. Данная ситуа­ция иллюстрируется на рис. 5.2. Каково максималь­ное значение X₁, такое, что, отправляясь с 1000 литрами горючего из точки 500— X₁, можно перевезти горючего в точку В столько, чтобы из точки В мы вылетели с 500 литрами горючего (т.е. как в случае k=1).

Один из способов определения приемлемого зна­чения Xi состоит в следующем. Заправляемся в точ­ке 500—X₁, едем X₁ километров до В и переливаем в хранили­ще все горючее, кроме X₁ литров, которые потребуют­ся для возвращения в точку 500-X₁. В этой точке бак становится пус­тым. Теперь наполняем его снова, проезжаем X₁ километров до В, забираем в В горючее, оставленное там, и из В едем в С с полным ба­ком. Общее пройденное расстояние состоит из трех отрезков по X₁ километров и одного отрезка ВС длиной 500 километров. Мы должны израсходовать каждую каплю топлива, чтобы сделать значение X₁ как можно боль­шим. Поэтому X₁ находим из уравнения

3 Õ₁ + 500 =1000 (литров);

его решение: Õ₁=500/3.

Таким образом, два бака (1000 литров) позволяют нам пролететь расстояние

D₂=500+X₁=500 (l+1/3) километров.

Заметим, что исходная предпосылка является недальновидной и грубой. Когда имеются в распоряжении k баков горючего, мы просто стараемся продвинуться назад как можно дальше от точки, найденной для k—1 баков.

Рассмотрим k=3. Из какой точки мы можем вылететь с 1500 литрами топлива так, что вертолет сможет доставить 1000 литров в точку 500—X₁? Возвращаясь к рис. 5.2, мы ищем наибольшее значение Х₂, такое, что, выезжая с 1500 литрами топлива из точки 500—X₁—Х₂, мы можем доставить 1000 литров в точку 500—X₁. Мы выезжаем из точки 500—X₁—Х₂, доезжаем до 500—X₁, переливаем все горючее, кроме Х₂ литров, и возвращаемся в точку 500—X₁—Х₂ с пустым баком. Повторив эту процедуру, мы затратим 4Х₂ литров на проезд и оставим 1000 — 4Х₂ литров в точке 500—X₁. Теперь в точке 500—X₁—Х₂ осталось ровно 500 литров. Заправляемся послед­ними 500 литрами и едем в точку 500—X₁, израсходовав на это Х₂ литров.

Теперь мы находимся в точке 500— X₁, затратив на проезд 5Х₂ литров топлива. Здесь оставлено в общей сложности 1500—5Х₂ литров. Это количество должно быть равно 1000 литрам, т. е. Х₂==500/5. Из этого заключаем, что 1500 литров позволяют нам пролететь

D = 500 + X₁+Õ₂ = 500 (l+1/3+1/5) километров.

Продолжая индуктивно процесс отрабатывания назад, получаем, что n баков горючего позволяют нам пролететь Dn километров, где

D =500 (1+1/3+1/5+...+1/(2n-1)).

Нужно найти наименьшее значение п, при котором Dn = 1000. Простые вычисления показывают, что для n=7 имеем D₇=977,5 километра, т. е. семь баков, или 3500 литров, топлива дадут нам возможность пролететь 977,5 мили. Полный восьмой бак — это было бы уже больше, чем нам надо, чтобы перевезти 3500 литров из точки А в точку, отстоящую на 22,5 мили (1000—977,5) от А. Читателю представляется самостоятельно убедиться в том, что для доставки 3500 литров топ­лива к отметке 22,5 мили достаточно 337,5 литра. Таким образом, для того чтобы пересечь на вертолете пустыню из А в С, нужно 3837,5 литра горючего.

Теперь алгоритм транспортировки горючего может быть пред­ставлен следующим образом. Стартуем из А, имея 3837,5 литра. Здесь как раз достаточно топлива, чтобы постепенно перевезти 3500 литров к отметке 22,5 мили, где мы в конце концов окажемся с пустым баком и запасом горючего на семь полных заправок. Этого топлива достаточно, чтобы перевезти 3000 литров к точке, отстоящей на 22,5+500/13 километров от А, где бак машины будет опять пуст. После­дующие перевозки приведут нас к точке, отстоящей на 22,5+500/13+500/11 километров от А, с пустым баком машины и 2500 литрами.

Продолжая таким образом, мы продвигаемся вперед благодаря анализу, проведенному методом отрабатывания назад. Вскоре мы окажемся у отметки 500 (1—1/3) = 1000/3 километров с 1000 литрами топ­лива. Затем мы перевезем 500 литров в В, зальем их в бак вертолета и долетим без остановки до С. Рис.5.3 иллюстрирует весь этот процесс.

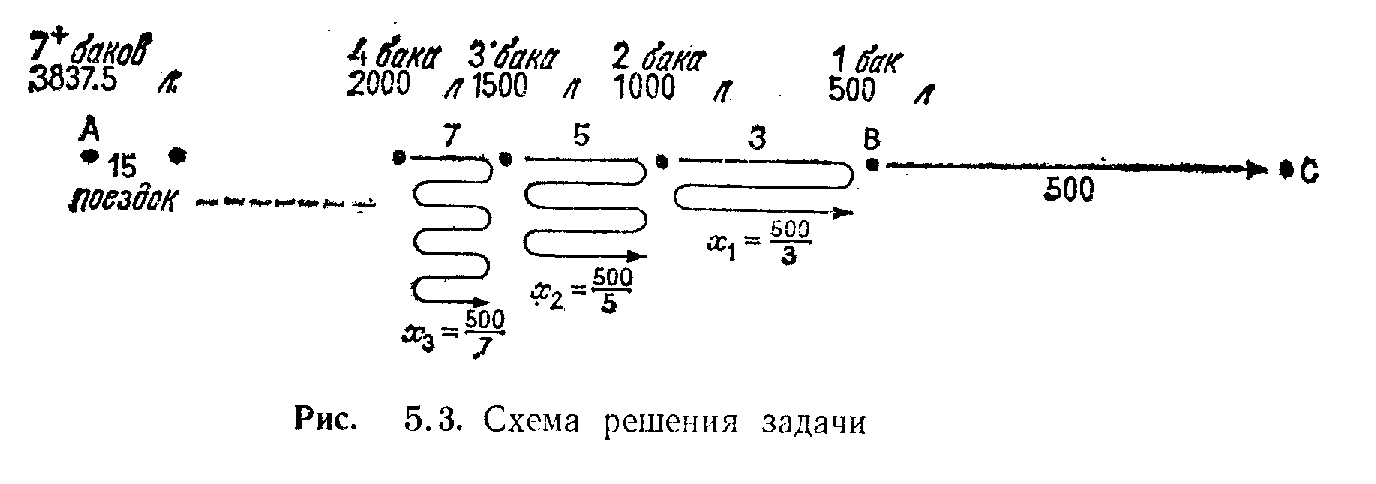
Для тех, кто знаком с бесконечными рядами, заметим, что Dn есть n-я частная сумма нечетного гармонического ряда. Поскольку этот ряд расходится, алгоритм дает возможность пересечь любую пустыню. Как можно модифицировать этот алгоритм для того, чтобы оставить достаточно горючего в различных точках пустыни для воз­вращения в А?

Возникает вопрос, можно ли пролететь 1000 километров, затратив меньше чем 3837,5 литра горючего. Оказывается, что нельзя. Доказатель­ство этого факта довольно сложно. Однако можно высказать следую­щий, довольно правдоподобный довод. Очевидно, мы действуем наилучшим образом для k=1. При k=2 мы используем наш план для k=1 и затем вводим в действие второй бак горючего для того, чтобы оказаться как можно дальше от В. Исходная предпосылка для k баков заключается в том, что мы знаем, как действовать наилучшим образом в случае с k—1 баками, и отодвигаемся как можно дальше назад с помощью k-ro бака.

5.2 Метод эвристики

Метод решения задачи на интуитивном уровне, правильность которого доказать не возможно, но тем не менее, который дает хорошее, но не обязательно оптимальное решение называют эвристический метод.

Или другими словами эвристический алгоритм, или эвристика, определяется как алго­ритм со следующими свойствами:

1. Он обычно находит хорошие, хотя не обязательно оптимальные решения.

2. Его можно быстрее и проще реализовать, чем любой известный точный алгоритм (т. е. тот, который гарантирует оптимальное решение).

Понятия «хороший» н «обычно» в свойстве 1 меняются от задачи к задаче.

Возникает вопрос почему решение многих задач основано на этом методе, который дает не обязательно оптимальное решение. Дело в том, что иногда оптимальное решение достичь не возможно, либо процесс достижения оптимального решения настолько трудоемок, что проще получить пусть не оптимальное, но достаточно хорошее решение за значительно меньшее время. Например, если для решения задачи все известные точные алгоритмы требуют нескольких лет машинного времени, то мы можем охотно принять любое нетривиальное приближенное решение, которое может быть получено за разумное время. С другой стороны, имея быстрое, близкое к оптимальному решение, мы можем стремиться все же к точному решению.

Хотя не существует универсальной структуры, которой можно описать эвристические алгоритмы, многие из них основываются или на методе частных целей, или на методе подъема.

Рассмотрим при каких случаях возникает эвристический алгоритм.

- когда решение задачи не достижимо, или очень трудоемко традиционными методами;

- когда не возможно доказать правильность используемого алгоритма

Итак, для первого случая общий подход к построению эвристических алгоритмов заключается в перечислении всех требований к точному решению и разделении требований на два класса, например:

1. Те, которые легко удовлетворить.

2. Те, которые не так легко удовлетворить.

Или

1. Те, которые должны быть удовлетворены.

2. Те, по отношению к которым мы могли бы пойти на компромисс.

Тогда цель построения алгоритма — создать алгоритм, гарантиру­ющий выполнение требований 1-го класса, но не обязательно 2-го. Это не означает, что для удовлетворения требований 2-го класса не делается никаких попыток, это просто означает, что не может быть дано никаких гарантий, что они будут удовлетворены.

По отношению ко второму случаю можно сказать, что часто очень хорошие алгоритмы должны рассматриваться как эвристические. Например, предположим, что мы построили быстрый алгоритм, который, кажется, работает на всех тестовых задачах, но мы не можем доказать, что алгоритм правильный. Пока не дано такое доказательство, алгоритм следует рассматривать как эвристику.

В качестве примера рассмотрим следующий «грубый» алгоритм решения задачи коммивояжера, рассмотренному нами в главе 3.

Транспортная задача.

Приближенный алгоритм решения транспортной задачи. Решить задачу ком­мивояжера с N городами, последовательно двигаясь из города n в город n+1, соблюдая условие: стоимость проезда между городом n и новым городом n+1 минимальна. Индекс n изменяет значение от 1 до N.

Шаг 0. [Инициализация, т. е. установка в начальное состояние]

TOUR=0; МIN=¥.

Шаг 1. [Посещение всех городов]

For I=1 to (N—1)

Шаг 2. [Выбор следующего пути]

Определение минимальной стоимости проезда из города n во все

оставшееся города и определение города n+1.

Шаг 3. [Вычисление стоимости проезда]

Вычисляем стои­мость COST (Т (Р)) как сумму всех стоимостей от начальной точки до точки V+1.

Шаг 4. [Окончание цикла]

Ш аг 5 [Вывод результатов и окончание программы]

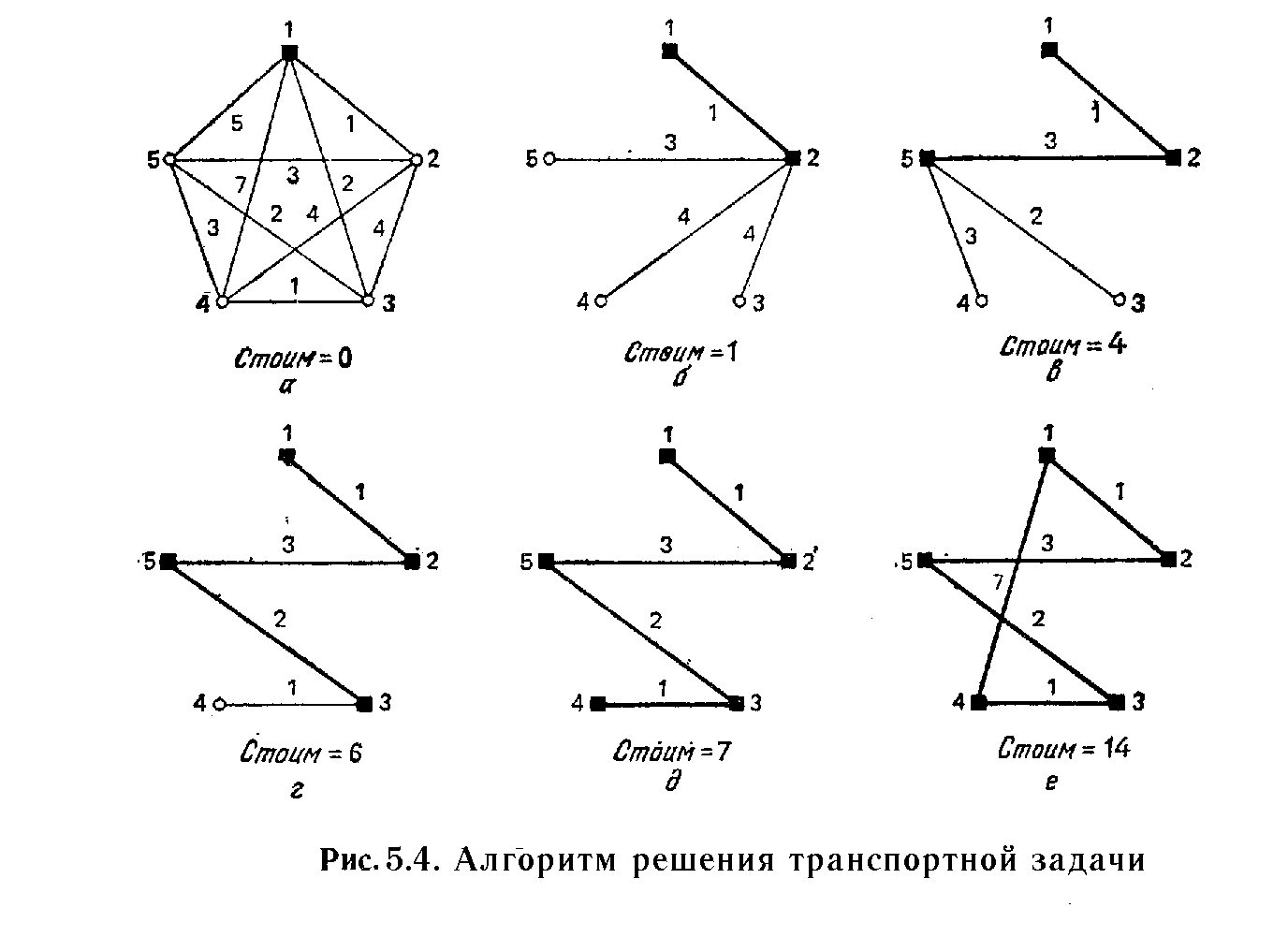
На рис. 5.4а изображена сеть городов с соответствующими стоимостями проезда, а рис.5.4б - 5.4е иллюстрируют построение тура коммивояжера для эвристического алгоритма, начинающегося с вершины 1; пройдённые вершины обозначены черным квадратиком, а непройденные — кружком.

Алгоритм эвристики дает общий проезд со стоимостью 14, а в гл.3 решение исчерпывающего алгоритма дает общий проезд со стоимостью 13. Ясно, что эвристический алгоритм не всегда находит общий проезд с минимальной стоимостью.

Обычно грубые алгоритмы очень быстры и интуитивно привлека­тельны, но, как мы заметили, они не всегда дают оптимальное решение задачи. Нам повезло, и мы смогли легко найти контрпример для алгоритма эвристического метода транспортной задачи. Однако не всегда можно легко показать, что грубый алгоритм не работает. Разумеется, если мы считаем, что наш грубый алгоритм работает всегда, то мы должны доказать, что это так.

Эвристический алгоритм транспортной задачи основан на идее подъема. Цель — найти общий проезд с минимальной стоимостью. Задача сведена к набору частных целей — найти на каждом шаге «самый дешевый» город, чтобы посетить его следующим. Алгоритм не строит плана вперед; текущий выбор де­лается безотносительно к последующим выборам.

Оптимальное решение задачи коммивояжера имеет два основных свойства:

1. Оно состоит из множества ребер, вместе представляющих общий проезд.

2. Стоимость никакого другого общего проезда не будет меньше данного.

Эвристический алгоритм рассматривает свойство 1 как «обязательное», или «легкое», требование, а свойство 2 — как «трудное», относительно которого можно пойти на компромисс.

Пример с пятью городами на рис. 5.4 сразу показывает, что ал­горитм приведенный выше не гарантирует свойство 2. Однако на шаге 2 делается некоторая попытка снизить стоимость общего проезда.

Конечно, для алгоритма с помощью метода эвристики легко написать программу, но яв­ляется ли он быстрым? Для произвольной задачи коммивояжера с п городами требуется операций пропорционально N², чтобы прочесть или построить матрицу стоимостей С. Поэтому нижняя граница сложности любого алгоритма, способного дать нетривиальное возможное решение этой задачи по существующему методу равна N². Поэтому представленный алгоритм настолько быстрый, насколько возможно.

По-видимому, представленный алгоритм — это хороший эвристический алго­ритм. Конечно, понятие «хороший» относительно. Поскольку алго­ритм «исчерпывающий коммивояжер» слишком неэффективен, эпитет «хороший» может просто указывать на тот факт, что представленный алгоритм — наилучший из имеющихся для больших (в разумных пределах) значений N.

5.3 Программирование с отходом назад

Часто в программировании встречаются задачи в которых необходимо перебрать все возможные комбинации некоторой величины, или ситуация поиска некоторого значения из списка параметров. Встает задача как правильно организовать перебор комбинаций или осуществить поиск, не пропустив при этом ни одного значения. Причем, очень часто складывается ситуацию в которой, при таком переборе необходимо учесть те комбинации на которые условиями задачи поставлен запрет.

Один из методов такой организации вышеназванных процессов является программирование с отходом назад.

Метод разработки алгоритма, известный как программирование с отходом назад, можно описать как организованный исчерпывающий поиск, который часто позволяет избежать исследования всех возмож­ностей.

Этот метод особенно удобен для решения задач, требующих проверки потенциально большого, но конечного числа решений.

Для более полного представления этой задачи ее целесообразно посмотреть на примере задачи о замке с шифр.

Задача о замке

В качестве примера рассмотрим комбинационный замок допустим для вело­сипеда, состоящий из набора N переключателей, каждый из которых может быть в положении «вкл» или «выкл». Замок открывается только при одном наборе положений переключателей, из которых не менее [N/2] (целая часть от N/2) находятся в положении «вкл». Предпо­ложим, что мы забыли эту комбинацию, а нам надо отпереть замок. Предположим также, что мы готовы перепробовать (если необходимо) все комбинации. Нам нужен алгоритм для систематического генери­рования этих комбинаций. Если проигнорировать условие [N/2], то для замка существует 2^N возможных комбинаций. Однако условие [N/2J позволит отбросить (или лучше не генерировать) многие комбинации.

Промоделируем каждую возможную комбинацию вектором из N нулей и единиц. На i-м месте будет 1, если i-й переключатель нахо­дится в положении «вкл», и 0, если i-й переключатель — в положении «выкл». Множество всех возможных N-векторов хорошо моделируется с помощью двоичного дерева. Каждая вершина k-го уровня этого дерева будет соответствовать определенному набору первых k компонент N-вектора. Две ветви, идущие вниз из вершины этого уровня, соответствуют двум возможным значениям (k+1)-й компоненты в N-векторе. У дерева будет N уровней. Рис. 5.5 на примере N=4 поясняет основную конструкцию.

Условие, заключающееся в том, что число переключателей в положении «вкл» должно быть не меньше [N/2], позволяет нам не образовывать части дерева, которые не могут привести к правильной комбинации. Например, рассмотрим вершину 00 на рис. 5.5. Так как правая ветвь (к 000) не может привести к допустимой комбинации, нет нужды ее формировать. Если какие-то вершины, следующие за рассматриваемой вершиной, не удовлетворяют ограничению задачи, то эти вершины не надо рассматривать. В данном случае никакие из вершин, находящихся внутри пунктирных линий, не нужно исследо­вать и даже формировать.

Теперь, воспользовавшись этой моделью двоичного дерева, можно изложить процедуру отхода назад для образования только тех ком­бинаций, в которых по крайней мере [N/2] переключателей нахо­дятся в положении «вкл». Алгоритм сводится к пересечению дерева.

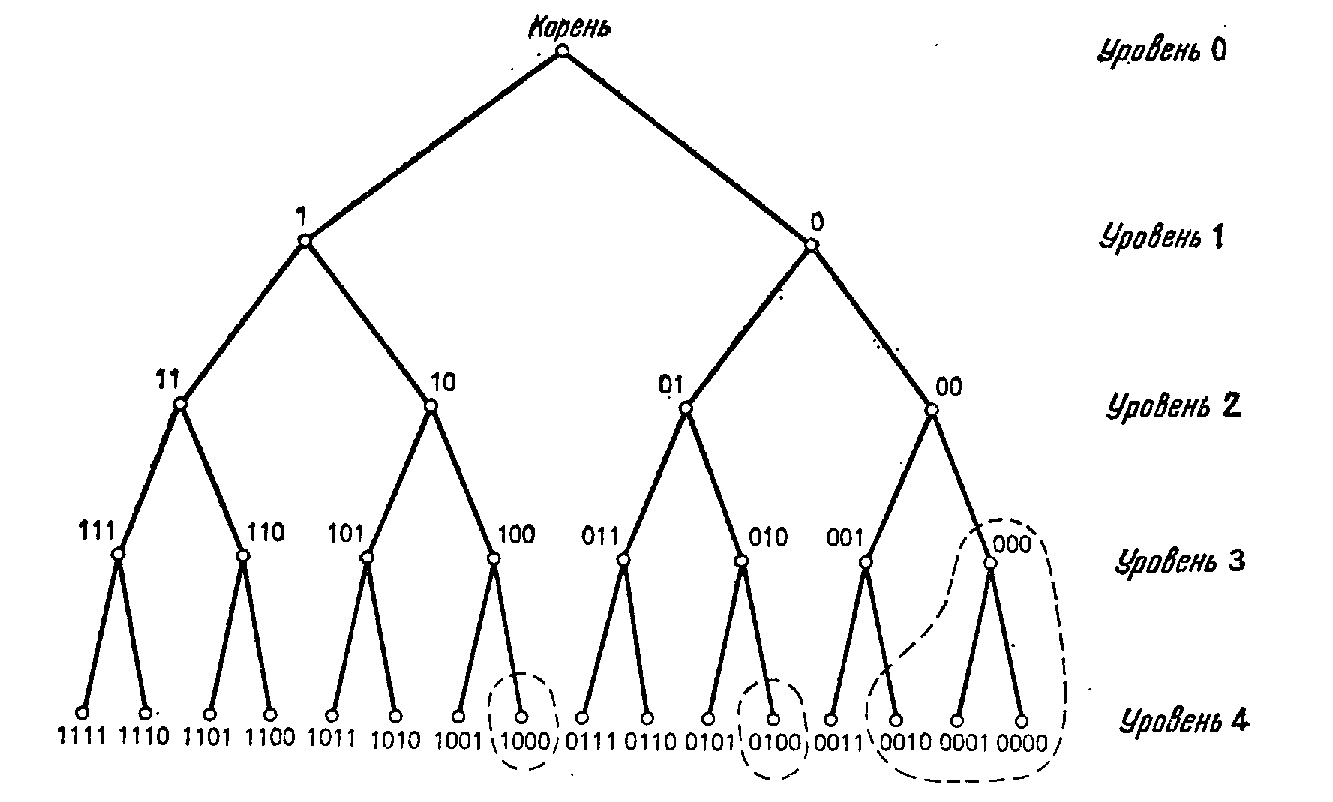
Рис. 5.5 Двоичное дерево, представляющее N-векторы из нулей и единиц.

Двигаемся вниз по дереву, придерживаясь левой ветви, до тех пор, пока это возможно. Достигнув конечной вершины, опробуем соот­ветствующую комбинацию.. Если она не подходит, поднимаемся на один уровень и проверяем, можем ли мы спуститься опять по другой ветви. Если это возможно, берем самую левую из неисследованных ветвей. Если нет, отходим вверх еще на один уровень и пытаемся спуститься из этой вершины. Перед спуском проверяем, можно ли удовлетворить условие об [N/2] включенных переключателях в последующих вершинах. В ситуации, изображенной на рис. 5.5, этот алгоритм просмотрит следующую последовательность вершин:

1111 Проверка этой комбинации.

0111 Отход, так как 1111 —конечная вершина.

1110 Спуск по единственной непросмотренной ветви вниз, про­верка этой комбинации.

0111 Снова отход.

0011 Отход дальше, так как из 0111 все ветви просмотрены.

0110 Спуск по единственной непросмотренной ветви.

1101 Проверка комбинации.

0110 Отход из 1101

1100 Проверка комбинации.

0110 Отход из 1100.

0011 Отход, так как все ветви просмотрены.

0001 Отход, так как все ветви просмотрены.

0010 Спуск по единственной непросмотренной ветви.

0101 Спуск по самой левой непросмотренной ветви.

1011 Проверка комбинации.

0101 Отход.

1010 Проверка комбинации.

0101 Отход.

0010 Отход.

0100 Спуск по единственной непросмотренной ветви.

1001 Проверка комбинации.

0100 Отход.

0010 Отход; заметим, что мы не опускаемся к 1000, так как эта вершина нарушает условие о том, что должно быть по край­ней мере две единицы.

0001 Отход.

Корень Отход.

0 Спуск по единственной непросмотренной ветви.

.

.

.

и т. д.

Алгоритм останавливается, когда мы возвращаемся к корню и не остается непросмотренных ветвей.

Этот простой пример иллюстрирует основные свойства, общие для всех алгоритмов с отходом назад. Если можно сформулировать задачу так, что все возможные решения могут быть образованы построением N-векторов, тогда ее можно решить при помощи процедуры с отходом.

5.4. Метод ветвей и границ

Метод, известный как метод ветвей и границ, похож на методы с отходами назад тем, что он исследует древовидную модель простран­ства решений и применим для широкого круга дискретных комбина­торных задач. Алгоритмы с отходами нацелены на то, чтобы найти одну или все конфигурации, моделируемые N-векторами, которые удовлетворяют определенным свойствам. Алгоритмы ветвей и границ ориентированы в большей степени на оптимизацию.

В этом методе определяется некая функция, как весовая числовая функция для различных вариантов решения задачи и вычисляется численные значения этой функции для различных вариантов решения. Цель — найти конфигурацию, на которой эта функция достигает максимального или минималь­ного значения. Сам же метод отыскания и построения такой функции получил название метод ветвей и границ. Такое название возникло в результате того, что в нем используется ветвление и вычисляются границы.

Рассмотрим более подробно что понимается под ветвлением и что понимается под границей.

Ветвление - это процесс разбиения всех вариантов решения задачи на два множества, таким образом, что какая-либо конкретная подзадача принадлежит только одному из этих множеств. В этом случае говорят, что ветвление происходит на этой подзадаче. Если пользоваться терминологией древовидной структуры, то говорят, что ветвление происходит на определенной ветви древовидной структуры.

 

Рис.5.6

На рис 5.6 показана древовидная структура, ветвление производится в точке Б при рассмотрении подзадачи Б, дальнейшее решение задачи пойдет либо по пути Б-В, либо по пути Б-Г. Ветвление происходит в точке Б и разбивается на два подмножества. Сущность ветвления заключается в том, что какая-то конкретная подзадача Б входит в множество 1 и не входит в множество 2 вариантов решения задачи.

Следующим шагом является вычисление нижних границ. Под этим понимается вычисления весовой функции для всей вариантов множества 1 или множества 2. Для каждого множества 1 или 2 существует конечное число вариантов решения, в которых весовая функция принимает определенные значения. Назовем из множество значений весовой функции 1 и 2, которые соответствуют множествам 1 и 2. Естественно, что для каждого из множеств весовой функции имеется определенная граница нижняя или верхняя, по которой происходит оценка дальнейшего пути решения задачи.

Другими словами, если нам необходимо минимизировать весовую функция и удалось доказать, что нижняя граница этой функции для множества 1 меньше чем нижняя граница из множества 1, то необходимо продвигаться по пути Б-В решения задачи.

Поясним это на примере.

Как конкретно определить подзадачу ветвления рассмотрим на примере транспортной задачи с коммивояжером, в которой очень хорошо работает алгоритм ветвей и границ. В данном разделе изложение будет вестись на примере этой задачи. Сделаем замечание, что алгоритмы ветвей и границ, как правило, бывают довольно сложны и представленный здесь — не исключение. Тем не менее, в некоторых случаях, его использование бывает очень эффективным. При помощи алгоритмов ветвей и границ удалось решить большой круг разнообразных серь­езных практических задач, но эти алгоритмы редко оказыва­ются простыми.

Напомним, что задача заключается в нахождении в торговом участке коммивояжера пути из N городов с наименьшей стоимостью. Каждый город входит в путь только один раз. В терминах сетей в сети городов надо найти покрывающий цикл наименьшей стоимости. Имеется матрица С, каждый элемент которой Сij равен стоимости (обычно в единицах времени, денег или расстояния) прямого проезда из города I в город J. Задача называется симметричной, если Сij=Cji для всех i и j, т. е. если стоимость проезда между каждыми двумя городами не зависит от направления. Предположим, что Сii = ¥ для всех i.

Алгоритмы ветвей и границ для задачи коммивояжера могут быть сформулированы разными способами. Авторы излагаемого алгорит­ма — Литл, Мерти, Суини и Карел. Это своего рода классика.

Во-первых, рассмотрим ветвление. На рис. 5.7а показана мат­рица стоимостей для асимметричной (несимметричной) задачи комми­вояжера с пятью городами, представленной на рис.5.7б. Обратите внимание на то, что мы пользуемся направленной сетью, чтобы ука­зать стоимости, так как стоимость проезда из города i прямо в город j не обязательно такая же, как стоимость проезда из города j в город i. Корень нашего поискового дерева будет соответствовать множеству «всех возможных вариантов», (в дальнейшем назовем каждый вариант решения задачи туром) т. е. эта вершина представляет множество всех 4! возможных туров в нашей задаче с пятью городами. В общем случае для любой асимметричной задачи с N городами корень будет представлять полное множество R всех (N—1)! возможных туров. Ветви, выходящие из корня, определяются выбором одного ребра, скажем (i, j).

Наша цель состоит в том, чтобы разделить множество всех туров на два множества: одно, которое, весьма вероятно, содер­жит оптимальный тур, и другое, которое, вероятно, не содержит. Для этого выбираем ребро (i,j); оно, как мы надеемся, входит в оп­тимальный тур, и разделяем R на два множества {i,j} и {i,j}. В мно­жество {i, j} входят туры из R, содержащие ребро (i, j), а в {i,j} — не содержащие (i,j).

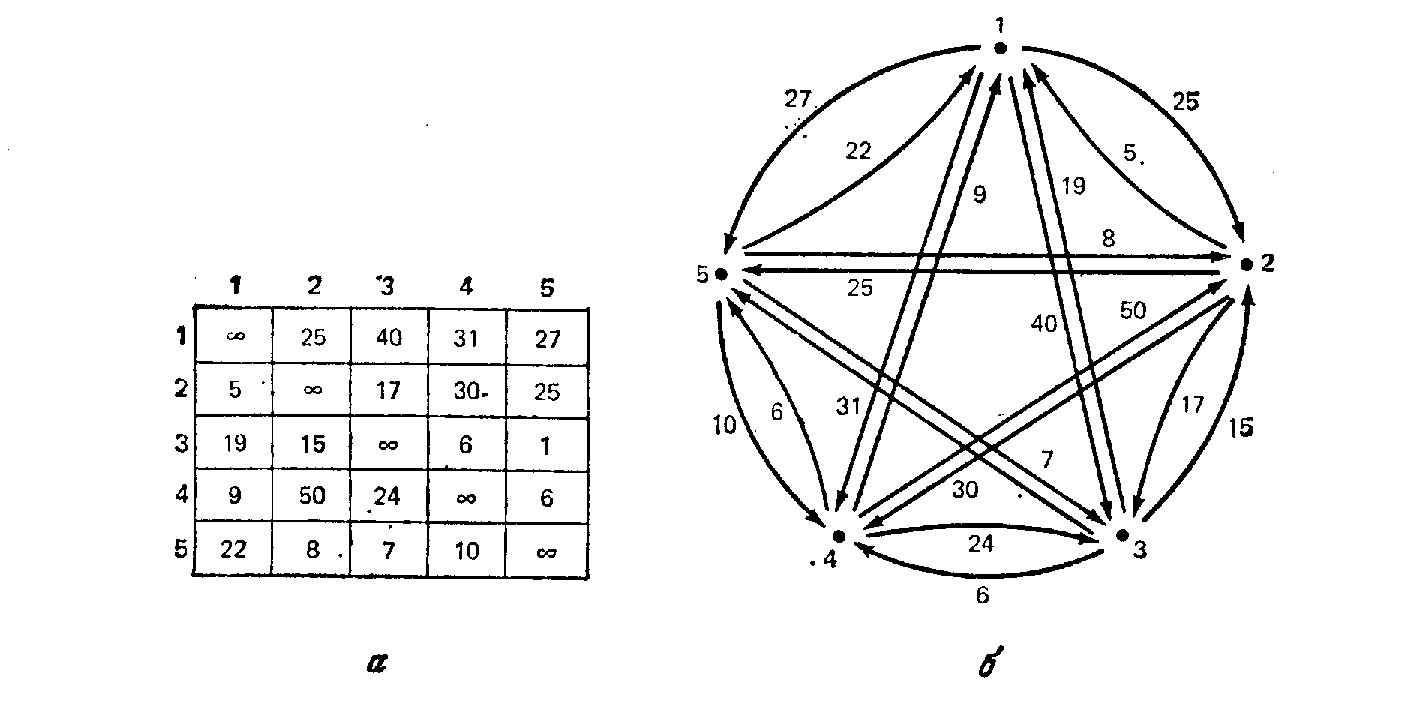
Рис. 5.7 Задача коммивояжера: (а) матрица стоимостей; (б) сеть из пяти городов.

Предположим, в нашем примере мы производим ветвление на ребре (i, j) = (3,5), имеющем наименьшую стоимость во всей матрице. Корень и первый уровень дерева пространства решений будут тогда такими, как показано на рис.5.8 Заметим, что каждый тур из R содержится только в одном множестве уровня 1. Если бы мы как-то могли сделать вывод, что множество {3,5} не содержит оптимального тура, то нам нужно было бы исследовать только множество {3, 5}.

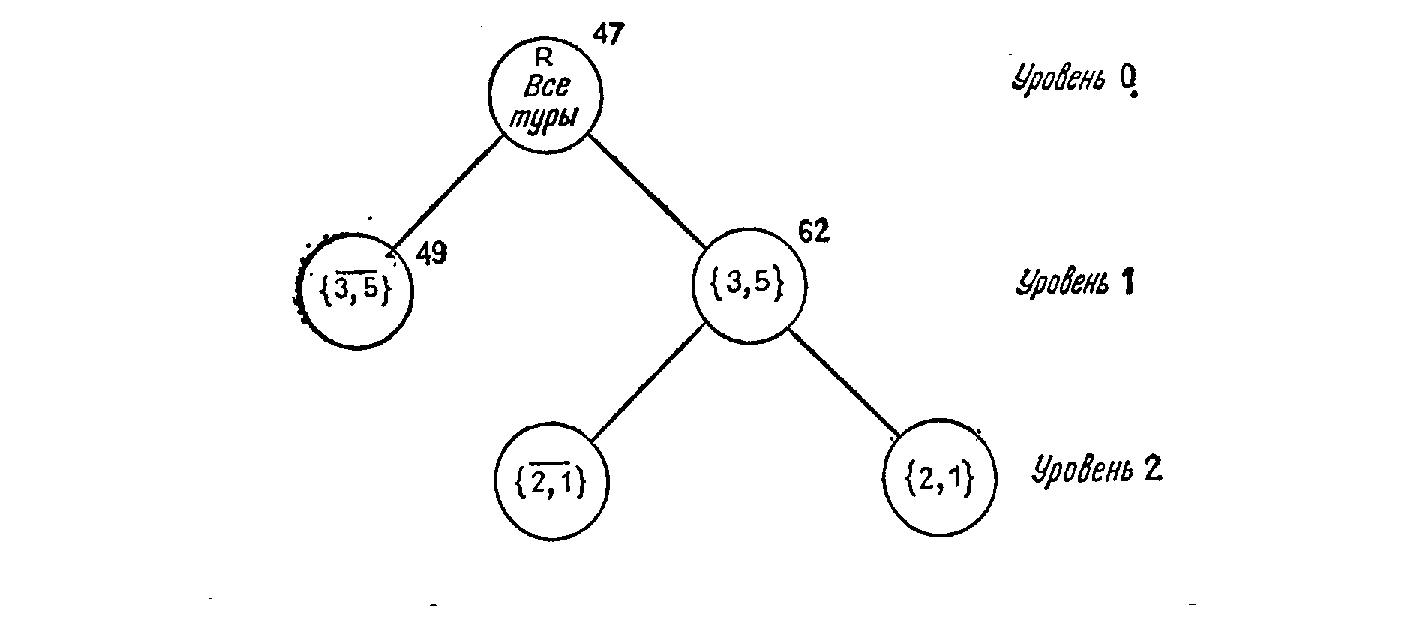
Рис. 5.8. Построение дерева поиска по методу ветвей и границ.

Затем разделяем множество {3, 5} таким же образом, как и множе­ство R. Следующее по дешевизне ребро в матрице — это ребро (2, 1) со стоимостью 5. Поэтому можно разделить множество {3, 5} на туры, включающие ребро (2, 1), и туры, не включающие этого ребра; это показано на уровне 2 на рис. 5.8. Путь от корня к любой вершине дерева выделяет определенные ребра, которые должны или не должны быть включены в множество, представленное вершиной дерева. Например, левая вершина уровня 2 на рис. 5.8 представляет множе­ство всех туров, содержащих ребро (3, 5) и не содержащих ребра (2, 1). Вообще, если Х — вершина дерева, a (i, j) — ребро ветвления, то обозначим вершины, непосредственно следующие за X, через Y и Y. Множество Y обозначает подмножество туров из Х с ребром (i,j), а множество Y — подмножество Х без (i, j).

Теперь, когда на примере мы пояснили, что такое ветвление, поясним, на этом же примере что подразумевается под вычислением границ.

Для каждой вершины дерева существует определенное множество решений, это множество укладывается в некоторые границы. Решения задачи мы связывает с весовой функцией. Для нашего случая эта функция представляет собой общую стоимость проезда. И поскольку для каждой вершины дерева может быть определенное множество решений, следовательно, для каждой вершины имеется определенное множество значений функций стоимости. Это множество значений имеет границы - верхнюю и нижнюю. Для нашей задачи о минимальной стоимости проезда, нас будет интересовать нижняя граница функции стоимостей.

Вычис­ление этих нижних границ — основной фактор, дающий экономию усилий в любом алгоритме типа ветвей и границ. Поэтому особое внимание следует уделить получению как можно более точных границ. Причина этого следующая. Предположим, что мы получили нижнюю границу стоимостей на одной вершине m, а на другой М и выполняется условие М>m, то исследованию должна быть подвергнута вершина стоимости m. и все следующие за ней.

Основной шаг при вычислении нижних границ известен как при­ведение. Оно основано на следующих двух соображениях:

1. В терминах матрицы стоимостей С каждый полный тур содержит только один элемент (ребро и соответствующую стоимость) из каждого столбца и каждой строки. Заметим, что обратное утверждение не всегда верно. Множество, содержащее один и только один элемент из каждой строки и из каждого столбца С, не обязательно представ­ляет тур. Например, в задаче, изображенной на рис. 5.7, множе­ство {(1, 5), (5, 1), (2, 3), (3, 4), (4, 2)} удовлетворяет этому условию, но не образует тура.

2. Если вычесть константу h из каждого элемента какой-то строки или столбца матрицы стоимостей С, то стоимость любого тура при новой матрице С' ровно на h меньше стоимости того же тура при матрице С. Поскольку любой тур должен содержать ребро из данной строки или данного столбца, стоимость всех туров уменьшается на h. Это вычитание называется приведением строки (или столбца).

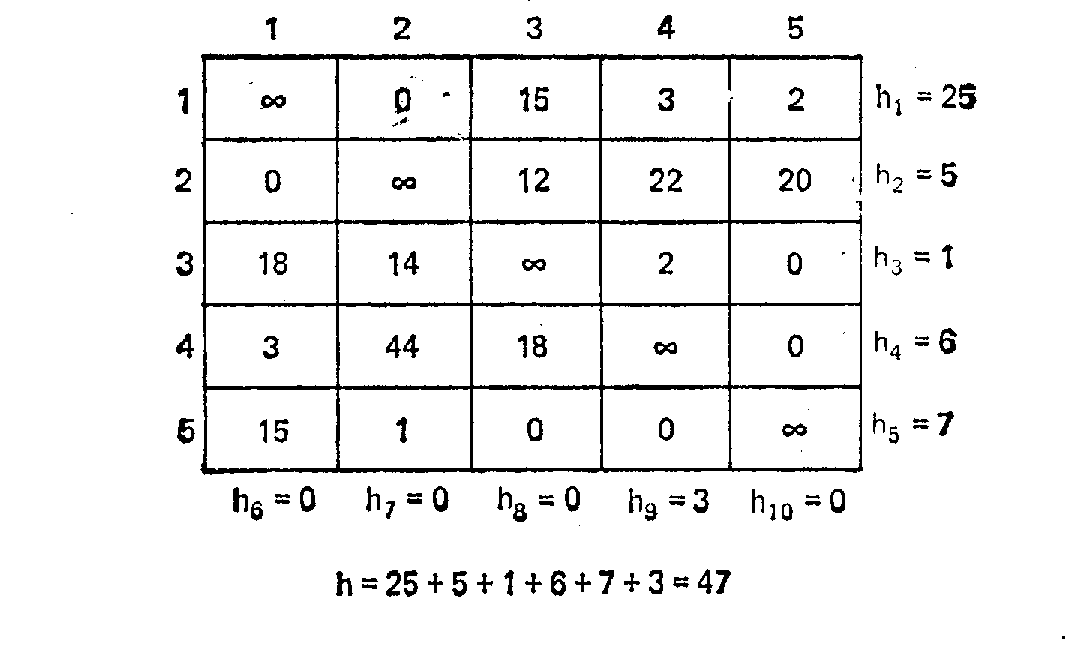
Рис. 5.9. Приведение матрицы стоимостей, показанной на рис.5.7 а.

Под приведением всей матрицы стоимостей С понимается следую­щее. Последовательно проходим строки С и вычитаем значение наи­меньшего элемента Hi каждой строки из каждого элемента этой строки. Потом то же самое делаем для каждого столбца. Если для некоторого столбца или строки Hi=0, то рассматриваемый столбец или строка уже приведены, и тогда переходим к следующему столбцу или строке.

Сумма всех Hi есть нижняя граница стоимостей, обозначим ее как H

Полученную в результате матрицу стоимостей назовем приведенной из С. На рис.5.9 показано приведение матрицы стоимостей, изобра­женной на рис. 5.7а. Значения Hi, даны в конце каждой строки и столбца (строки и столбцы последовательно перенумерованы).

Общее приведение составляет H=47 единиц. Следовательно, ниж­няя граница стоимости любого тура из R также равна 47. Эта граница указана около корня дерева на рис. 5.8. Рассмотрим нижние границы для вершин уровня 1, т. е. для множеств {3,5} и {3,5}. Вычислим их нижние границы.

Дата добавления: 2014-12-16