Постановка задачи множественной линейной регрессии

Понятие функции нескольких переменных

Множественная линейная регрессия

До сих пор мы касались вопросов, связанных с исследованием функции одной переменной, т.е. изучали совместное изменение двух переменных, одна из которых зависела от другой. Значением независимой переменной полностью определялось значение зависимой переменной, или функции. На практике значения географических переменных определяются обычно влиянием не одного, а нескольких объясняющих факторов. Например, хотя продуктивность водоема и зависит от продолжительности солнечного освещения, но очевидно, что это не единственный определяющий фактор, здесь важны и интенсивность освещения, и загрязненность водоема, и его географическое расположение, а также целый ряд дополнительных факторов. Таким образом, независимых переменных часто оказывается несколько, и для определения значения функции необходимо установить значения, совместно принимаемые всеми этими независимыми переменными. В таком случае зависимость y=f(x) означает, что х – вектор, содержащий m компонентов: x=(x_1, x₂,..., x_m).

Пусть в результате измерений в процессе опыта получена таблица некоторой зависимости f:

x1			...
x2			...
...	...	...	...	...
xm			...
y=f(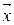)	y1	y2	...	yn

Требуется найти формулу, выражающую эту зависимость аналитически, т.е. найти функцию заданного вида y=F(x_1, x₂,..., x_m), которая в точках x_1, x₂,... x_n принимает значения, как можно более близкие к значениям
y₁, y₂,... y_n.

Мы будем говорить только о линейной зависимости у от х, то есть о множественной линейной регрессии. Теоретически уравнение y=F(x) имеет вид:

y=a₀+a₁x₁₊ a₂ x₂ +... +a_mx_m.

Здесь а – вектор неизвестных параметров размерности (m+1).

Мы ограничимся рассмотрением частного случая m=2. Тогда приближающая функция примет следующий вид:

F(x) =a₀+a₁x₁₊a₂ x₂.

Пусть имеется n наблюдений вектора х и зависимой переменной у. Для того, чтобы формально можно было решить задачу, то есть найти некоторый наилучший вектор параметров, должно быть n і m+1. Если это условие не выполняется, то можно найти бесконечно много разных векторов коэффициентов, при которых линейная формула связывает между собой х и у для имеющихся наблюдений абсолютно точно. Если в частном случае n=m+1 (например, при m=2 и n=3), то оценки коэффициентов а рассчитываются единственным образом – путем решения системы линейных уравнений y_j=a₀+a₁x_1j+a₂x_2j; j=1,...3. Графически это означает, что через три точки наблюдения в трехмерном пространстве можно провести единственную плоскость, определяемую параметрами a₀, a₁, a₂. Если число наблюдений больше минимально необходимого, то есть n>3, то уже нельзя подобрать линейную формулу, в точности удовлетворяющую всем наблюдениями, и возникает необходимость оптимизации, то есть выбора наилучшей формулы-приближения для всех наблюдений.

Более подробно с вопросом приближения функций нескольких переменных можно ознакомиться в [13, 18].

Глава 2. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

Из курса физики хорошо известен принцип сохранения энергии в замкнутой системе. При исследовании природных зависимостей любые изменения энергии системы почти всегда приводят к необходимости вычисления различного рода интегралов от соответствующих функций. Известное из курса математического анализа вычисление определенного интеграла по формуле Ньютона-Лейбница 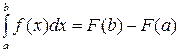реализовать на практике оказывается не всегда возможно. Например, может случиться, что первообразная F(x) не выражается через элементарные функции или через другие достаточно изученные функции либо выражается слишком сложно. В этих случаях приходится обращаться к методам приближенного интегрирования, т.е. к методам, позволяющим найти численное значение определенного интеграла приближенно с любой степенью точности.

Дата добавления: 2014-12-16