Разложение функций в ряд Фурье

Постановка задачи гармонического анализа

Из простейших периодических функций могут быть составлены более сложные. При этом составляющие синусоидальные величины должны быть разных частот, так как сложение синусоидальных величин одной и той частоты не дает ничего нового, а приводит к синусоидальной величине той же частоты.

Естественно, встает обратный вопрос: можно ли данную периодическую функцию f(t) периода Т представить в виде суммы конечного или хотя бы бесконечного множества синусоидальных величин. Как известно из классического анализа, по отношению к достаточно широкому классу функций на этот вопрос можно дать утвердительный ответ, то есть для них имеет место разложение в тригонометрический ряд или ряд Фурье.

Геометрически это означает, что график периодической функции получается путем наложения ряда синусоид. Если же истолковать каждую синусоидальную величину механически, как представляющую гармоническое колебательное движение, то можно также сказать, что в этом случае сложное колебание (каковыми являются все колебания, встречающиеся в природе), характеризуемое функцией f(t), разлагается на отдельные гармонические колебания. В связи с этим отдельные синусоидальные величины, входящие в состав тригонометрического ряда, называют гармоническими составляющими функции f(t), или просто ее гармониками (первой, второй и т.д.) Сам процесс разложения периодической функции на гармоники носит название гармонического анализа [27].

Итак, гармоническим анализом называют операцию разложения заданной периодической функции f(x) в ряд Фурье. Если функция f(x) задана аналитически, то задача ее гармонического анализа полностью решается с помощью известных из классического анализа формул Эйлера-Фурье для вычисления коэффициентов ряда Фурье. Однако в огромном числе практических задач подлежащая анализу функция f(x) оказывается заданной в виде таблицы, полученной в результате измерений, или в виде кривой, вычерченной самопишущим прибором. Тогда точное вычисление коэффициентов Фурье по формулам Эйлера-Фурье невозможно. Таким образом, в нашем случае задача гармонического анализа заключается в построении практически удобных методов для приближенного определения коэффициентов ряда Фурье или для непосредственного вычерчивания гармоник различных порядков для функции, заданной таблично.

Будем предполагать, что функция f(x) – периодическая, с периодом 2p (f(x+2р)=f(x)). Как известно, это всегда обеспечивается соответствующим изменением масштаба по оси Ох.

Основная задача гармонического анализа состоит в представлении функции f(x) в виде ряда:

. (1)

Полагая

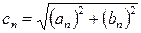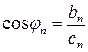, , , (2)

ряд (1) можно переписать в виде:

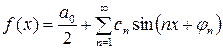(3)

Здесь с_n – амплитуда гармоники, j_n – фаза. Коэффициенты ряда (1) – ряда Фурье – определяют по формулам Эйлера-Фурье:

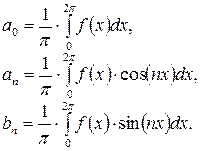(4)

Пусть промежуток от 0 до 2p разделен точками

x₁, x₂, …, x_k-1 (x_i=2pi/k)

на k равных частей и пусть известны соответствующие ординаты –

y₀, y₁, y₂,…, y_k-1, y_k=y₀.

Тогда для вычисления интегралов в формулах (4) можно применить различные приближенные методы. Так, по формуле трапеций получим:

.

Отсюда в силу того, что y₀=y_k,

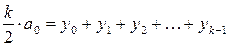. (5)

Аналогично для определения коэффициентов a_n и b_n формула трапеций дает:

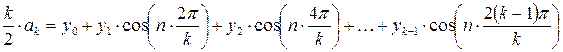, (6)

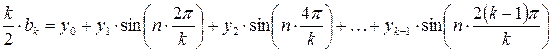, (7)

Окончательно получим:

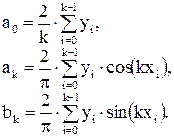
Последние формулы носят название формул Бесселя. Они могут быть получены из формул для коэффициентов Фурье (4) функции f(x), если вычислять входящие в них интегралы приближенно, используя формулу трапеций, полагая f(0)=f(2p) [4].

Заметим, что значения а₀, a_k, b_k, полученные по формулам Бесселя, будут близки к значениям коэффициентов Фурье функции только при относительно небольших к. В остальных случаях расхождение будет больше.

ЛАБОРАТОРНАЯ РАБОТА №7

Задание: Разложить заданную функцию в ряд Фурье.

Образец выполнения задания

Зададим функцию таблично

N:= 100

a1:= 1 a2:=.5 a3:= -.1

i:= 1.. N

xi:= i × dt значения аргумента

y_i:= a1×sin(x_i) + a2×sin(4×x_i) + a3×cos(5×x_i) значения функции, являющейся суммой трех гармонических колебаний.

Графическое представление заданной функции подтверждает наличие периодических составляющих:

Воспользуемся формулами Бесселя для вычисления коэффициентов a₀, a_k, b_k:

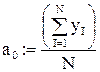
n:= 15 k:= 1.. n Значение 15 выбрано в Связи с возможностью РС

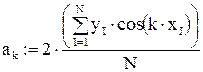
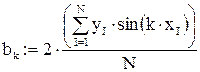
Учитывая, что при небольших к коэффициенты a₀, a_k, b_k будут близки к коэффициентам Фурье функции f(x), получим:

i:= 1.. N

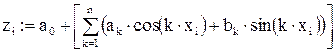
Графическое представление полученной функции (на рис. 15 представлены различные виды приближающей функции в зависимости от значения n):

Таким образом, графики иллюстрируют близость заданной функции и приближающего ее тригонометрического ряда.

Глава 5. СЕТЕВОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ

Выполнение комплексных научных исследований, а также проектирование и строительство промышленных, сельскохозяйственных и транспортных объектов требуют календарной увязки большого числа взаимосвязанных работ, выполняемых различными организациями. Составление и анализ соответствующих календарных планов представляют собой весьма сложную задачу, при решении которой применяются так называемые методы сетевого планирования. По существу, этот метод дает возможность определить, во-первых, какие работы или операции из числа многих, составляющих проект, являются «критическими» по своему влиянию на общую календарную продолжительность проекта, и, во-вторых, каким образом построить наилучший календарный план проведения всех работ по данному проекту с тем, чтобы выдержать заданные сроки при минимальных затратах.

Первый вариант этого метода был разработан в 1957 году американским ученым Дж.Е. Келли и М.Р. Уокером и был назван СРМ (от начальных букв выражения «Critical Path Method», означающего «Метод критического пути»). Примерно в то же время независимо от СРМ появилась система PERT («Program Evaluation and Review Technique», что означает «Техника обзора и оценки программ»). В результате дальнейшего развития эти системы превратились в совокупную методику построения графиков – сетевое планирование и управление.

Идея сетевого метода очень проста. Она основана на графическом изображении комплекса работ с любой степенью их детализации и на выполнении элементарных арифметических операций по расчету параметров и анализу сетевых графиков.

Дата добавления: 2014-12-16