Статистические меры информации. При статическом вероятностном подходе получение конкретного количества информации рассматривается как результат определенного выбора среди возможных

При статическом вероятностном подходе получение конкретного количества информации рассматривается как результат определенного выбора среди возможных сообщений. Получатель информации может заранее знать или угадать ее часть. Когда приходит сообщение о часто происходящих событиях, вероятность появления которых Р стремится к единице, то такое сообщение малоинформативно. Столь же малоинформативны в среднем сообщения о событиях, вероятности которых стремятся к нулю, т.е. о почти невозможных событиях, поскольку сообщения о таких событиях поступают чрезвычайно редко.

События можно рассматривать как возможные исходы некоторого опыта. Все исходы составляют полную группу событий, или ансамбль. Ансамбль характеризуется тем, что сумма вероятностей всех сообщений в нем равна единице, то есть

.

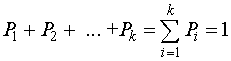Рассмотрим сложные сообщения, составляемые из п элементов, каждый из которых является независимым и выбирается из алфавита, содержащего т букв, с вероятностями выбора элементов 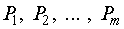соответственно. Предположим, что в некоторое сообщение вошло 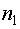элементов 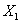алфавита, элементов 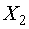и т.д. Такое сообщение характеризуется таблицей.

Тип элемента				...		...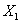
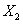
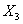
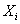
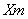
Число элементов				...		...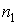
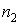
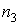
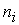
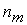
Вероятности выбора элементов				...		...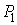

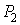
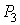
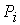
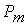
Вероятность того, что в сообщение войдут 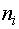элементов 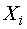равняется 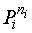, а вероятность образования сообщения из 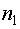, , ,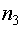..., ,..., 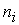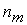элементов будет равна

Р= .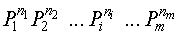

При большой длине п источником будут формироваться типичные сообщения, в которых относительная частота появления отдельных элементов 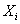стремится к вероятности появления этих элементов, то есть

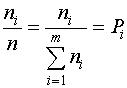
а вероятности появления типичных сообщений Р будут одинаковы и могут быть найдены из (1.1), (1.2):

Р= .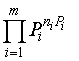

Определим число типичных сообщений:

,

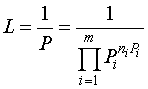так как суммарная вероятность всех типичных сообщений стремится к единице при увеличении длины сообщений.

Хотя число возможных сообщений 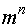, источник практически будет вырабатывать только L типичных сообщений, а вероятность появления остальных сообщений стремится к нулю.

Найдем количество информации I, содержащейся в одном сообщении:

I= log L= -log .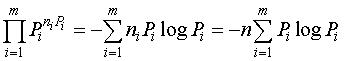

Данное выражение (формула Шеннона) дает более полное представление об источнике информации, чем аддитивная мера (мера Хартли). Поясним это на следующем примере. Если мы подбрасываем монету, то получим сообщение из двух возможных состояний (орел или решка), то есть, алфавит сообщений из двух букв. Если подбрасываем кубик, одна грань которого голубая, а остальные грани окрашены в розовый цвет, то здесь также имеем алфавит из двух букв (голубой или розовый). Чтобы записать полученный текст (сообщение), в обоих случаях достаточно одной двоичной цифры на букву (п= 1, т= 2).

По Хартли здесь в обоих случаях

I= n .

Но мы знаем, что в первом случае вероятность каждого исхода опыта равна 0,5 (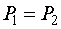 =0,5). А во втором случае 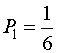и 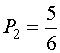соответственно. Мера Хартли не учитывает этого.

При равновероятности символов (частный случай) формула Шеннона вырождается в формулу Хартли:

I= - n .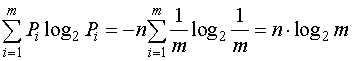

Для случая с монетой:

I= -1 .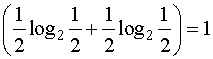

Для случая с кубиком:

I= -1 .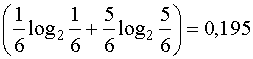

Дата добавления: 2014-12-16