Обобщение на двумерный случай

Одномерное вейвлетное преобразование Хаара легко переносится на двумерный случай. Это обобщение весьма важно, поскольку преобразование будет применяться к изображениям, которые имеют два измерения. Здесь снова производится вычисление средних и полуразностей. Существует много обобщений этого преобразования. Здесь мы остановимся на двух подходах, которые называются стандартное разложение и пирамидальное разложение.

Стандартное разложение начинается вычислением вейвлетных преобразований всех строк изображения. К каждой строке применяются все итерации процесса, до тех пора, пока самый левый элемент каждой строки не станет равен среднему значению чисел этой строки, а все остальные элементы будут равны взвешенным разностям. Получится образ, в первом столбце которого стоит среднее столбцов исходного образа. После этого стандартный алгоритм производит вейвлетное преобразование каждого столбца. В результате получится двумерный массив, в котором самый левый верхний угловой элемент равен среднему всего исходного массива. Остальные элементы верхней строки будут равны средним взвешенным разностям, ниже стоят разности средних, а все остальные пикселы преобразуются в соответствующие разности.

Пирамидальное разложение вычисляет вейвлетное преобразование, применяя итерации поочередно к строкам и столбцам. На первом шаге вычисляются полусуммы и полуразности для всех строк (только одна итерация, а не все вейвлетное преобразование). Это действие производит средние в левой половине матрицы и полуразности - в правой половине. На втором шаге вычисляются полусуммы и полуразности для всех столбцов получившейся матрицы.

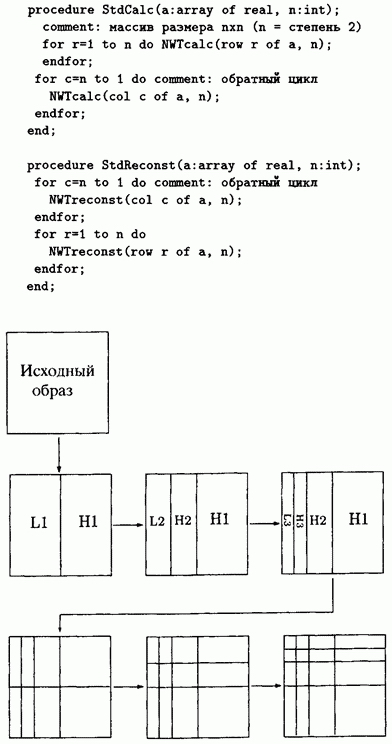
В итоге в левом верхнем квадранте будут стоять средние четырех квадрантов исходного образа, а в остальных квадрантах будут находиться соответствующие полу разности. Шаги 3 и 4 оперируют со строками и столбцами, в результате чего средние величины будут сконцентрированы в левой верхней подматрице (одной шестнадцатой всей исходной таблицы). Эти пары шагов применяются к все более и более маленьким подматрицам, до тех пор пока в верхнем левом углу не будет стоять среднее всей исходной матрицы, а все остальные пикселы преобразуются в разности в соответствии с ходом алгоритма.

Описанные преобразования являются ортогональными. Они преобразуют пикселы изображения во множество чисел, из которых некоторые числа будут большими, а остальные маленькими. Вейвлетные преобразования, подобные преобразованию Хаара, работают иначе, они являются под диапазонными. Они разбивают образ на подобласти, из которых одна область содержит большие числа (средние значения в случае преобразования Хаара), а другие области состоят из малых чисел (разностей в нашем случае). Однако эти области, называемые поддиапазонами, не просто являются семействами больших и малых чисел. Они отражают различные геометрические свойства трансформируемого образа. Чтобы пояснить эту особенность, изучим маленькое равномерное изображение, содержащее вертикальную и горизонтальную линию.

Правая часть преобразованной матрицы (содержащая разности) в основном состоит из нулей. В этом отражается равномерность образа. Однако след от вертикальной линии вполне заметен (подчеркнутые числа обозначают отрицательные разности).

Верхний правый поддиапазон содержит след от вертикальной линии, а в нижнем левом поддиапазоне отчетливо виден след от горизонтальной линии. Обозначим эти поддиапазоны HL и LH, соответственно (см. рис. 4.35, хотя имеется некоторое разночтение в использовании обозначений разными авторам). Нижний правый поддиапазон обозначим НН, на котором отражаются диагональные особенности образа (в нашем случае отсутствующие). Самым интересным остается верхний левый поддиапазон, целиком состоящий из средних величин (он обозначается LL). Этот квадрант, являющийся уменьшенной копией исходного образа с пониженным качеством, содержит следы от обеих линий.

На рисунке ниже показан типичный результат пирамидального вейвлетного преобразования. Рисунок выбран состоящим в основном из горизонтальных, вертикальных и наклонных линий, чтобы были заметны особенности пирамидального преобразования. Верхний левый поддиапазон, содержащий средние значения, подобен исходному образу, а три остальных квадранта (поддиапазона) показывают детали изображения. Верхний правый поддиапазон отражает вертикальные детали изображения, нижний левый - горизонтальные, а нижний правый содержит детали наклонных линий. Все изображение трансформируется в последовательность поддиапазонов, отражающих особенности по горизонталям, вертикалям и диагоналям, а самый верхний левый квадратик, содержащий усредненное изображение, стягивается в один единственный пиксел.

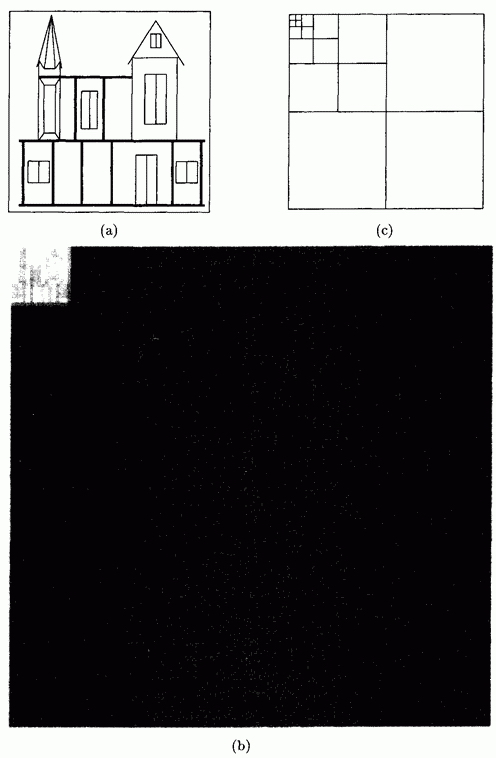
Независимо от метода (стандартного или пирамидального) в результате преобразования получается одно большое среднее число в верхнем левом углу матрицы образа, а все остальные элементы матрицы являются малыми числами, разностями или средними разностей. Теперь этот массив чисел можно подвергнуть сжатию с помощью подходящей комбинации методов RLE, кодирования Хаффмана или других известных алгоритмов. Если допустима частичная потеря информации, то наименьшие разности можно дополнительно квантовать или просто обнулить. Этот шаг даст длинные серии нулей, к которым метод RLE можно применить с еще большей эффективностью.

Дата добавления: 2014-12-16